吳恩達機器學習之單變數線性迴歸實現部分
阿新 • • 發佈:2018-12-06
C++實現
- 程式碼實現
“linear_regression.h”
//單變數線性迴歸模型 struct elem_var1 { double x, y; //訓練集元素資料:自變數、因變數 }; class var1_lin_reg { public: var1_lin_reg(const elem_var1* p, int size, double rate); //初始化 ~var1_lin_reg(); //析構 double cost_fuction(); //返回當前預測方程對應代價函式的值 void update(); //同時更新方程引數 void find(); //最小化代價函式,找到收斂點時對應的方程引數 void get_par(double &_par1, double &_par0); //獲得當前方程的引數 double est_val(double x); //使用擬合後的迴歸方程進行預測 private: const elem_var1 * tran_set; //訓練集 int setsize; //訓練集資料量 double par1, par0; //單變數線性迴歸方程:h(x)=par1*x+par0 double learn_rate; //學習速率 };
“linear_regression.cpp”
//單變數線性迴歸 var1_lin_reg::var1_lin_reg(const elem_var1* p, int size, double rate) {//引數列表:訓練集陣列地址,訓練集資料量,學習速率 setsize = size; //獲取訓練集大小 tran_set = p; //指標指向訓練集陣列 learn_rate = rate; //設定學習速率 par1 = 0; //線性迴歸方程引數初始化為0 par0 = 0; } var1_lin_reg::~var1_lin_reg() { tran_set = NULL; setsize = 0; } double var1_lin_reg::cost_fuction() {//假設函式為h(x)=kx+b double hx, sum = 0; for (int i = 0;i < setsize;i++) { hx = par1 * tran_set[i].x + par0; sum += (hx - tran_set[i].y)*(hx - tran_set[i].y); } return (sum / 2.0 / setsize); } void var1_lin_reg::update() {//兩引數(par0和par1)同時更新(關鍵是對微分項的處理) double hx, sum0 = 0, sum1 = 0; for (int i = 0;i < setsize;i++) { hx = par1 * tran_set[i].x + par0; sum0 += hx - tran_set[i].y; sum1 += (hx - tran_set[i].y)*tran_set[i].x; } sum0 = learn_rate * sum0 / (double)setsize; sum1 = learn_rate * sum1 / (double)setsize; par0 -= sum0; par1 -= sum1; } void var1_lin_reg::find() {//尋找代價函式最小化時對應的單變數線性迴歸函式的引數(代價函式收斂點) double cost_pre, cost_last; cost_pre = cost_fuction(); update(); //更新引數 cost_last = cost_fuction(); while (cost_pre != cost_last) {//尋找收斂點 cost_pre = cost_last; update(); cost_last = cost_fuction(); } //獲得假設函式最優擬合時的引數 } void var1_lin_reg::get_par(double &_par1,double &_par0) {//獲取迴歸方程引數 _par1 = par1; _par0 = par0; } double var1_lin_reg::est_val(double x) {//返回預測值 find(); //獲得假設函式最優擬合時的引數 double hx; hx = par1 * x + par0; //計算估計值 return hx; }
“主函式部分”
#include "linear_regression.h" using namespace std; int main() { elem_var1 transet[200]; memset(transet, 0, sizeof(transet)); int size; double x; double par1, par0; cout << "請輸入訓練集容量:"; cin >> size; cout << "請輸入訓練集資料:" << endl; for (int i = 0;i < size;i++) { cout << "資料項" << i + 1 << ": "; cin >> transet[i].x >> transet[i].y; } var1_lin_reg obj1(transet, size, 0.001); cout << "請輸入待預測資料:"; cin >> x; cout << "預測資料為:" << obj1.est_val(x) << endl; obj1.get_par(par1, par0); if(par0>0) cout << "h(x)=" << par1 << "*x+" << par0 << endl; else { if(par0<0) cout << "h(x)=" << par1 << "*x" << par0 << endl; else cout << "h(x)=" << par1 << "*x" << endl; } return 0; }
-執行結果
以吳恩達老師的ex1data1.txt資料集為例:
用octave資料視覺化:
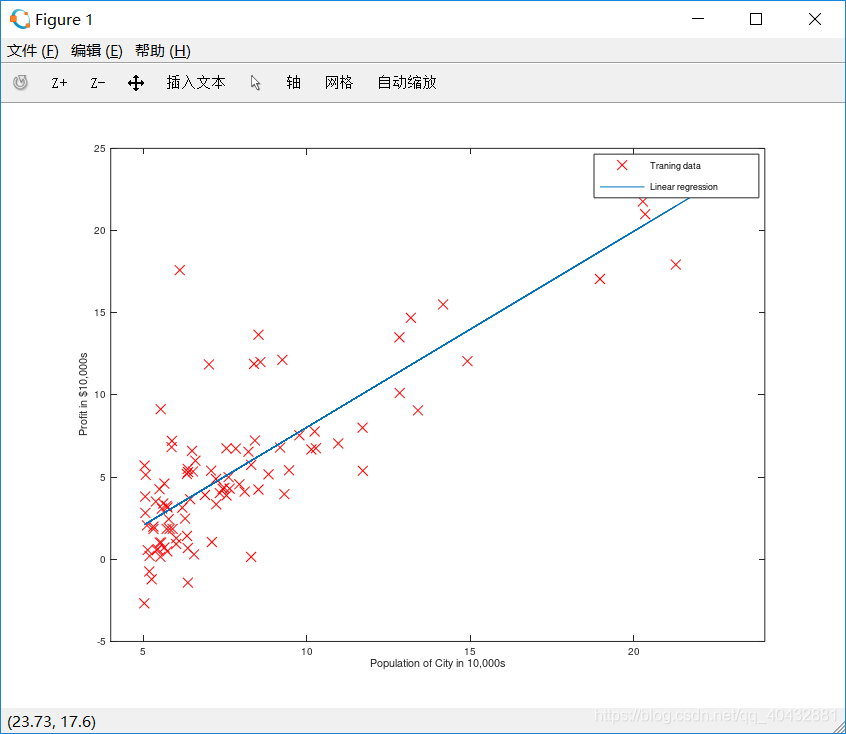
線性擬合應該還可以。。。。。。
