(本文圖片及被*標註內容來自CSDN部落格：pi9nc)

基本概念—二分圖

二分圖：是圖論中的一種特殊模型。若能將無向圖G=(V,E)的頂點V劃分為兩個交集為空的頂點集，並且任意邊的兩個端點都分屬於兩個集合，則稱圖G為一個為二分圖。

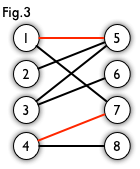
匹配：一個匹配即一個包含若干條邊的集合，且其中任意兩條邊沒有公共端點。如下圖，圖3的紅邊即為圖2的一個匹配。

匹配邊/匹配點：包含在匹配中的邊及其端點。

非匹配邊/非匹配點：不包含在匹配中的邊及其端點。

最大匹配：所含邊數最多的匹配稱為最大匹配。*

基本概念—匈牙利演算法

交替路：從一個未匹配點出發，依次經過非匹配邊、匹配邊、非匹配邊...形成的路徑叫交替路。*

增廣路：從一個未匹配點出發，走交替路，如果途徑另一個未匹配點（出發的點不算），則這條交替路稱為增廣路（agumenting path）。

匈牙利演算法

由增廣路的性質，增廣路中的匹配邊總是比未匹配邊多一條，所以如果我們放棄一條增廣路中的匹配邊，選取未匹配邊作為匹配邊，則匹配的數量就會增加。匈牙利演算法就是在不斷尋找增廣路，如果找不到增廣路，就說明達到了最大匹配。

演算法模板(鄰接表 & C++)

#include<iostream>
using namespace std;

const int N=20000,M=20000;

struct edge{int u,v; edge *next;}e[M],*P=e,*point[N];
int Link[N],used[N],n,m;

inline void add_edge(int u,int v)
{
	++P;
	P->u = u; P->v = v; P->next = point[u]; point[u] = P;
}

bool dfs(int u)
{
	for(edge *j=point[u];j;j=j->next)
	{
		if(used[j->v])	continue;
		used[j->v]=true;
		if(Link[j->v]==0 || dfs(Link[j->v]))
		{
			Link[j->v]=u;
			return true;
		}
	}
	return false;
}

int main()
{
	//讀入資料
	memset(Link,0,sizeof(Link));
	int cnt=0;
	for(int i=1;i<=n;i++)
	{
		memset(used,0,sizeof(used));
		if(dfs(i))	cnt++;
	}
	cout<<cnt<<endl;
}