STFT和聲譜圖,梅爾頻譜(Mel Bank Features)與梅爾倒譜(MFCCs)
最近小編在做ASC(Acoustic Scene Classification)問題,不管是用傳統的GMM模型,還是用機器學習中的SVM或神經網路模型,提取聲音特徵都是第一步。梅爾頻譜和梅爾倒譜就是使用非常廣泛的聲音特徵形式,小編與它們鬥爭已有一段時間了,在此總結一下使用它們的經驗。
STFT和聲譜圖(Spectrogram)
聲音訊號本是一維的時域訊號,直觀上很難看出頻率變化規律。如果通過傅立葉變換把它變到頻域上,雖然可以看出訊號的頻率分佈,但是丟失了時域資訊,無法看出頻率分佈隨時間的變化。為了解決這個問題,很多時頻分析手段應運而生。短時傅立葉,小波,Wigner分佈等都是常用的時頻域分析方法。
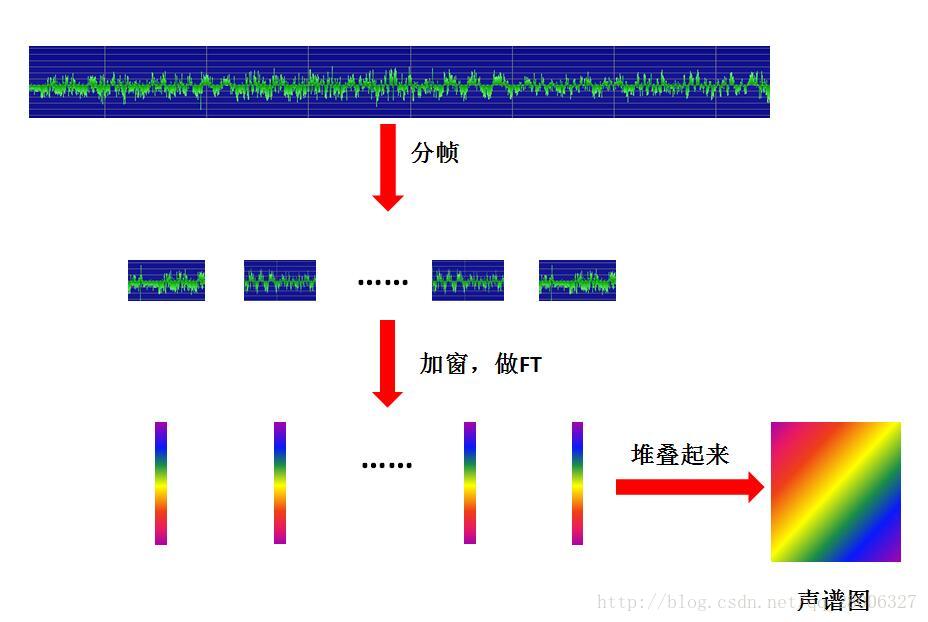
短時傅立葉變換(STFT)是最經典的時頻域分析方法。傅立葉變換(FT)想必大家都不陌生,這裡不做專門介紹。所謂短時傅立葉變換,顧名思義,是對短時的訊號做傅立葉變化。那麼短時的訊號怎麼得到的? 是長時的訊號分幀得來的。這麼一想,STFT的原理非常簡單,把一段長訊號分幀、加窗,再對每一幀做傅立葉變換(FFT),最後把每一幀的結果沿另一個維度堆疊起來,得到類似於一幅圖的二維訊號形式。如果我們原始訊號是聲音訊號,那麼通過STFT展開得到的二維訊號就是所謂的聲譜圖。
有很多工具方便地支援STFT展開,如果你是和小編一樣是python愛好者,可以使用scipy庫中的signal模組。如果你想做STFT分解的音訊訊號(wav檔案)的路徑存在path變數中,可通過下面的程式碼得到STFT資料。
import wavio
import numpy as np
from scipy import signal
wav_struct=wavio.read(path)
wav=wav_struct.data.astype(float)/np.power(2,wav_struct.sampwidth*8-1)
[f,t,X]=signal.spectral.spectrogram(wav,np.hamming(1024),nperseg=1024,noverlap=0,detrend=False,return_onesided=True,mode='magnitude')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
關於signal模組中spectrogram的使用方法和各個引數的具體意義,參見https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.spectrogram.html#scipy.signal.spectrogram
梅爾頻譜和梅爾倒譜
聲譜圖往往是很大的一張圖,為了得到合適大小的聲音特徵,往往把它通過梅爾標度濾波器組(mel-scale filter banks),變換為梅爾頻譜。什麼是梅爾濾波器組呢?這裡要從梅爾標度(mel scale)說起。
梅爾標度,the mel scale,由Stevens,Volkmann和Newman在1937年命名。我們知道,頻率的單位是赫茲(Hz),人耳能聽到的頻率範圍是20-20000Hz,但人耳對Hz這種標度單位並不是線性感知關係。例如如果我們適應了1000Hz的音調,如果把音調頻率提高到2000Hz,我們的耳朵只能覺察到頻率提高了一點點,根本察覺不到頻率提高了一倍。如果將普通的頻率標度轉化為梅爾頻率標度,對映關係如下式所示: 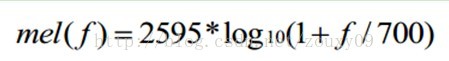
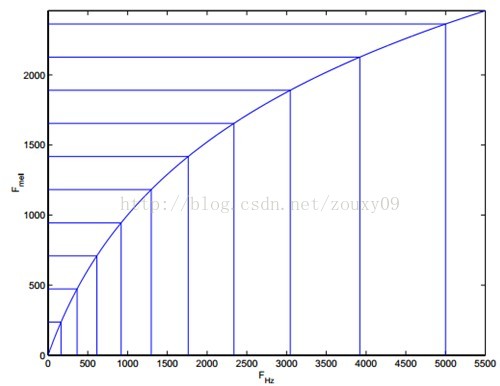
則人耳對頻率的感知度就成了線性關係。也就是說,在梅爾標度下,如果兩段語音的梅爾頻率相差兩倍,則人耳可以感知到的音調大概也相差兩倍。
讓我們觀察一下從Hz到mel的對映圖,由於它們是log的關係,當頻率較小時,mel隨Hz變化較快;當頻率很大時,mel的上升很緩慢,曲線的斜率很小。這說明了人耳對低頻音調的感知較靈敏,在高頻時人耳是很遲鈍的,梅爾標度濾波器組啟發於此。 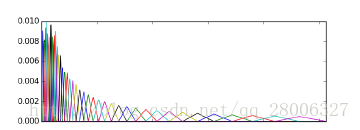
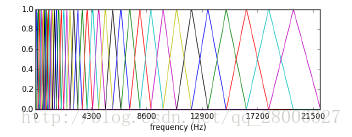
如上圖所示,40個三角濾波器組成濾波器組,低頻處濾波器密集,門限值大,高頻處濾波器稀疏,門限值低。恰好對應了頻率越高人耳越遲鈍這一客觀規律。上圖所示的濾波器形式叫做等面積梅爾濾波器(Mel-filter bank with same bank area),在人聲領域(語音識別,說話人辨認)等領域應用廣泛,但是如果用到非人聲領域,就會丟掉很多高頻資訊。這時我們更喜歡的或許是等高梅爾濾波器(Mel-filter bank with same bank height):
至於梅爾濾波器怎麼生成的(各個三角濾波器起始頻率和終止頻率怎麼得到,等面積梅爾濾波器最高門限值怎麼得到)這個問題,我列在後面的參考文獻和部落格可以回答你。但如果你只是想使用梅爾濾波器組得到梅爾頻率譜,並不關心它怎麼得到的,那麼你只需要關注下面的程式碼段:
import numpy as np
import librosa
melW=librosa.filters.mel(fs=44100,n_fft=1024,n_mels=40,fmin=0.,fmax=22100)
melW /= np.max(melW,axis=-1)[:,None]
melX = np.dot(X,melW.T)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
其中,變數X是上一小節程式碼段得到的聲譜,melX就是我們說的梅爾頻譜。librosa庫是python中的語音和訊號處理的專業庫,具體說明參見:http://librosa.github.io/librosa/generated/librosa.filters.mel.html#librosa.filters.mel
我們知道梅爾頻譜了,那麼梅爾倒譜是怎麼回事呢?
這裡涉及到倒譜分析的概念,在附錄一(大神zouxy09的部落格)介紹的很詳細了。記住一句話,在梅爾頻譜上做倒譜分析(取對數,做DCT變換)就得到了梅爾倒譜。這裡通過一段程式碼展示梅爾倒譜怎麼得到的:
import librosa
melM = librosa.feature.mfcc(wav,sr=44100,n_mfcc=20)- 1
- 2
而librosa.feature.mfcc這個函式內部是這樣的:
# -- Mel spectrogram and MFCCs -- #
def mfcc(y=None, sr=22050, S=None, n_mfcc=20, **kwargs):
if S is None:
S = logamplitude(melspectrogram(y=y, sr=sr, **kwargs))
return np.dot(filters.dct(n_mfcc, S.shape[0]), S)- 1
- 2
- 3
- 4
- 5
- 6
可以看出,如果只給定原始的時域訊號(即S引數為None),librosa會先通過melspectrogram()函式先提取時域訊號y的梅爾頻譜,存放到S中,再通過filters.dct()函式做dct變換得到y的梅爾倒譜系數。
感謝librosa可以使我們方便地提取這些有用的聲音特徵!!
附錄
【1】http://blog.csdn.net/zouxy09/article/details/9156785/
【2】http://blog.sina.com.cn/s/blog_892508d501012px5.html
【3】https://en.wikipedia.org/wiki/Mel-frequency_cepstrum