區域性一致性是一種正式定義我們希望網路保證的一致性數量的方法，因此，執行這種一致性級別的演算法將決定生成哪個網路。但是沒有提到演算法是如何執行的。規則迭代在另一方面解決了這個問題。約簡規則指定在哪些條件下以及在哪些約束條件下執行篩選操作。只有當約簡規則及其應用方式具有一些良好的性質時，網路生成的結果才能保證具有一定程度的區域性一致性等形式化性質。規則迭代方法最初由Montanari和Rossi以鬆弛規則的名義正式提出[96]。Benhamou等通過區間演算法interval arithmetics(即只減少邊界)研究規則迭代[10,11]。約束處理規則(Constraint Handling Rules, CHR)是一種基於約簡規則的程式語言(參見第二部分的[59]和第13章)。我基本上遵循Apt關於約簡規則概念的表述。

約簡規則只是一個將網路對映到另一個網路的函式，其中影象是輸入的收緊。

我們應該記住PN包含了所有緊繃N的網路(見定義3.13)。在大多數情況下，約簡規則是根據單個約束減少單個變數域的約簡步驟。我將它們命名為傳播器。

傳播器可以驗證一些屬性。

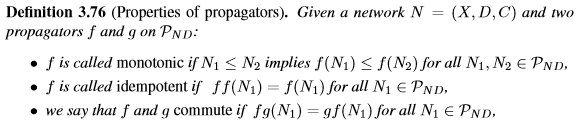
1）單調性  2）冪等  3）可交換

實踐中使用的大多數傳播器都滿足定義3.76的特性。其中單調性尤為有趣。我首先需要定義迭代和傳播器穩定性的含義。

PND中可能有許多網路對於給定的傳播器集是穩定的。但傳播子的單調性意味著只會產生其中的一個。

演算法3.8是以網路N和PND上的一組傳播子F作為輸入的過程。由於3.80號提案，我們保證它會終止。如果f中的所有f都是單調的，則演算法3.8的輸出是f在N上的最小固定點

有時，除了單調性之外，傳播子還具有其他一些特性。在這些情況下，演算法3.8可以被簡化，同時仍然保證產生相同的結果。

通過定義適當的傳播器集，我們可以獲得前幾節中介紹的大部分區域性一致性。例如，我們可以在網路N =(X,D,C)上實施弧一致性。我首先定義傳播器fi,j，使:

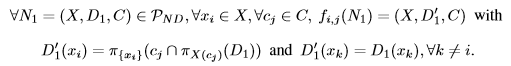
它們都是單調的。然後，泛迭代(N,FAC)終止於FAC的最小固定點，即N的圓弧一致閉包。

從[2]中可以看出，我們還可以通過定義同時涉及多個約束並改變約束集的單調傳播器集來增強高階一致性，例如路徑一致性。