改進csp回溯演算法效能的一個基本觀點是，區域性不一致會導致大量的抖動或無效率的搜尋[47,89]。區域性不一致性是某些變數的例項化，這些變數滿足相關約束，但不能擴充套件到一個或多個額外變數，因此不能成為任何解決方案的一部分。(區域性不一致不是好事;參見4.4節)。如果我們使用回溯搜尋來尋找解決方案，這種不一致性可能導致搜尋中出現許多死區，並導致許多徒勞的搜尋工作。這種見解導致:

1. 描述CSP區域性一致性水平的條件的定義
2. 約束傳播演算法的發展——這些演算法通過消除CSP中的不一致性來加強這些級別的區域性一致性
3. 有效的回溯演算法尋找解決csp的方案,保持在搜尋區域性一致性水平

在回溯搜尋中維護區域性一致性的一般方案是在搜尋樹中的每個節點上執行約束傳播。約束傳播演算法通過釋出排除或消除不一致的附加約束來消除區域性不一致。當在搜尋過程中使用時，約束會隨著搜尋在樹中的深入而在節點上釋出。但是在對某個節點進行回溯時，必須撤銷在該節點上釋出的約束。當在執行任何例項化或分支決策之前在搜尋樹的根節點上使用時，約束傳播有時稱為預處理階段preprocessing。

結合約束傳播的回溯搜尋有兩個重要優點。首先，在搜尋過程中消除不一致可以通過消除許多死端和簡化剩餘的子問題來顯著地修剪搜尋樹。在某些情況下，一個變數在約束傳播後會有一個空域;也就是說，沒有值滿足該變數的一元約束。在這種情況下，可以啟動回溯，因為在搜尋樹的這個分支上沒有解決方案。在其他情況下，變數的域將被縮小。如果一個域被簡化為一個值，那麼該變數的值是強制的，將來不需要對其進行分支。因此，在約束傳播之後可以更容易地找到CSP的解決方案，或者表明CSP沒有解決方案。其次，一些最重要的變數排序啟發式利用約束傳播收集的資訊來做出有效的變數排序決策

(這將在4.6節中進一步討論)。由於這些優點，現在標準的回溯演算法包含某種形式的約束傳播。

區域性一致性的定義至少可以分為兩類。首先，根據定義中的基本實體，可以將定義分為基於約束的定義和基於變數的定義。其次，區域性一致性的定義可以按照約束傳播過程中是否只需要釋出一元約束，或者是否有時需要釋出更高層次的約束來分類。在回溯的實現中，變數的域是可擴充套件表示的，通過更新域的表示可以非常有效地釋出和撤銷一元約束。在更高的高度上釋出和撤回限制是不那麼容易理解的，而且代價更大。如果只需要一元約束，則約束傳播有時稱為域過濾或域修剪。

將某種形式的約束傳播合併到回溯演算法中的想法來自幾個方向。Davis和Putnam[31]提出了單位傳播(unit propagation)

，這是一種專門用於SAT的約束傳播形式。Golomb和Baumert[57]可能是第一個非正式地描述通過在搜尋過程中加入某種形式的域修剪來改進一般回溯演算法的想法的人。Fikes的rf - arf[37]和Lauriere的Alice[82]使用了約束傳播技術，這兩種語言都用於陳述和求解csp。Gaschnig[47]是第一個提出回溯演算法的人，該演算法強制精確定義了每個節點的local一致性級別。Gaschnig的演算法使用了d路分支。Mackworth[89]概括了Gaschnig提出的回溯演算法，該演算法將case-analysis與約束傳播交叉(參見[89]獲取更多的歷史參考資料)。

自這項早期工作以來，出現了大量關於約束傳播和區域性一致性的文獻;超出了我可以合理討論的範圍。因此，我選擇了兩個具有代表性的例子:arc consistency和strong k-consistency。這些區域性一致性說明了上面給出的不同分類。同時，弧一致性是目前實踐中最重要的區域性一致性，也是目前最受關注的區域性一致性，而強k一致性在csp的理論方面發揮了重要作用。對於這些例子，我給出了局部一致性的定義，然後討論了在搜尋過程中保持這種級別的本地一致性的回溯演算法。我不討論任何特定的約束傳播演算法。本手冊有兩章專門討論這個主題(見第三章和第六章)。注意，許多約束傳播演算法的表示都是針對將在預處理階段使用該演算法的情況。但是，當在搜尋過程中使用以保持一定程度的本地一致性時，對約束傳播演算法的連續呼叫之間通常只會發生很小的變化。因此，人們也付出了很大的努力，使這種演算法逐漸增多，因此在搜尋過程中使用時效率更高。在提出結合約束傳播的回溯演算法時，我給出了回溯演算法的“純”形式，即在搜尋樹的每個節點上保持一致的區域性一致性。這只是為了便於表達。在實踐中，區域性一致性的實施水平和實施演算法是特定於每個約束的，並且在約束之間是不同的。一個例子是被廣泛使用的全不同全域性約束，其中快速演算法被設計用於強制執行許多不同級別的區域性一致性，包括圓弧一致性、範圍一致性、邊界一致性和簡單的值移除。然後，由建模人員決定執行哪一級的本地一致性。

4.3.1 Backtracking and Maintaining Arc Consistency 

Mackworth [89,90]定義了一種稱為弧一致性的區域性一致性。 給定約束C，符號t∈C表示元組t-對值（C）中的每個變數的值的賦值 - 滿足約束C.符號t [x]表示由元組t分配給變數x的值。

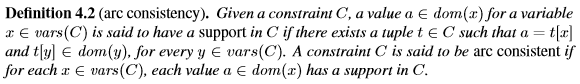
通過反覆從約束的變數域中刪除不受支援的值，可以使約束保持一致。請注意，本地一致性的定義是基於約束的，在CSP上強制執行arc一致性意味著迭代約束，直到不再對域進行任何更改為止。加強arc一致性的演算法已經被廣泛研究(見第3章和第6章)。對於任意約束的優化演算法，最壞情況下的時間複雜度為，其中r為約束的濃度，d為變數域的大小[101]。幸運的是，對於實踐中出現的約束類，幾乎總是可以做得更好。例如，在最壞的情況下，可以使所有不同的約束在時間內保持一致。Gaschnig[47]建議在回溯搜尋過程中保持圓弧一致性，並給出了第一個包含此思想的顯式演算法。在Sabin和Freuder[116]之後，我將用MAC表示這種演算法。MAC演算法對至少一個未例項化變數的約束保持arc一致性(見表4.1)。在搜尋樹的每個節點上，對CSP應用了一種增強圓弧一致性的演算法。由於arc一致性是在節點的父節點上強制執行的，所以最初的約束傳播只需要在分支策略釋出的約束上強制執行。反過來，這可能導致其他約束變得不一致，並且約束傳播將繼續，直到不再對域進行任何更改為止。如果由於約束傳播，域變為空，則分支為死端並被拒絕。如果沒有域是空的，則接受該分支，搜尋將繼續到下一個級別。

作為應用MAC的一個例子，考慮圖4.1所示的6皇后問題的回溯樹。MAC只訪問節點25，因為它發現這個節點是一個死端。圖4.2a中的板顯示了約束傳播的結果。帶陰影的帶數字的正方形對應於通過約束傳播從變數域中移除的值。如果由於樹的第i層的賦值而將值移除，則將值i放置在陰影正方形中。可以看出，在約束傳播之後，一些變數的域是空的。因此，賦值集{x1 = 2,x2 = 5}不能成為CSP解決方案的一部分。

當在搜尋過程中維護arc一致性時，從變數域中刪除的任何值都不參與CSP的任何解決方案。然而，並不是域中的所有值都一定是某個解決方案的一部分。因此，圓弧一致性傳播雖然可以減少搜尋空間，但不能消除所有可能的死端。假設如果變數域中的每個值都是CSP的某個解決方案的一部分，那麼CSP的域是最小的。顯然，如果約束傳播只會在搜尋樹的每個節點上留下最小的域，那麼搜尋將是自由回溯的，因為所選擇的任何值都將導致解決方案。不幸的是，找到最小域至少與解決CSP一樣困難。在對單個約束施加arc一致性之後，變數域中的每個值都是單獨考慮的約束的某個解決方案的一部分。找到最小域就相當於對CSP中約束條件的結合強制求弧一致性，這個過程在最壞情況下是n的指數，即CSP中的變數數量。因此，圓弧一致性可以看作是逼近最小域。

總的來說，在搜尋樹的每個節點上的約束傳播的成本，和最小域的近似的質量之間有一個權衡。一種改進這種近似的方法是使用更強的區域性一致性，例如單例一致性(參見第3章)，但是會增加約束傳播的成本。降低約束傳播成本的一種方法，就是對最小的區域進行較差的近似，並增加整體搜尋成本的增加，實際上就是限制弧一致性的應用。其中一種演算法稱為前向檢查。前向檢查演算法(FC)在約束條件上保持arc的一致性，而約束條件恰好是一個未例項化的變數(見表4.1)。在這些約束條件下，可以在O(d)時間內強制實現arc的一致性，其中d是未例項化變數的域的大小。Golomb和Baumert[57]可能是第一個非正式地描述前向檢查(在[57]中稱為排除)的人。McGregor[93]、Haralick和Elliott[63]給出了第一個顯式演算法。前向檢查最初是為二進位制約束提出的。這裡使用的對非二進位制約束的推廣是由於Van Hentenryck[128]。

作為應用FC的一個例子，考慮圖4.1所示的回溯樹。FC只訪問節點25、253、2531、25314和2536。圖4.2b的板子顯示了約束傳播的結果。搜尋過程中留下的空格對應於FC訪問的節點。

該領域的早期實驗工作發現，FC遠優於MAC[63,93]。然而，這種優勢在一定程度上是基準測試的易用性造成的。同時，近年來弧線一致性傳播演算法也得到了許多實際的改進，特別是在增量方面。結果表明，回溯演算法在搜尋過程中保持了完整的圓弧一致性，在實踐中被認為是非常重要的。一個例外是廣泛使用的DPLL演算法[30,31]，這是一種專門針對CNF格式SAT問題的回溯演算法(見表4.1)。DPLL演算法採用單元傳播，有時稱為布林約束傳播，作為其約束傳播機制。可以看出，單位傳播等價於對SAT問題的前向檢驗。進一步可以看出，弧一致性對這些問題的修剪量與前向檢驗的修剪量相等。因此，前向檢查是SAT問題上的約束傳播的正確水平。

前向檢驗只是限制電弧一致性傳播的一種方法;許多變化是可能的。例如，可以對具有不同數量的未例項化變數的約束保持arc一致性。Bessi 'ere等人考慮了這些可能性。在指定應該傳播哪些約束時，還可以考慮未例項化變數的域的大小。作為第三種選擇，可以對約束傳播演算法本身以及它如何遍歷約束設定特別的限制[63,104,117]。

另一種限制弧一致性應用的方法是限制弧一致性的定義，這種方法可以通過限制傳播哪些約束來實現，也可以通過限制傳播本身來實現。一個重要的例子是邊界一致性。假設變數的域又大又有序，並且變數的域由區間(域內的最小值和最大值)表示。使用邊界的一致性,而不是要求每個值∈dom(x)支援的約束,我們只問最小值和最大值都有一個支援的約束。雖然一般來說，邊界一致性比弧一致性弱，但已經證明邊界一致性對於算術約束和全域性約束是有用的，因為它有時可以更有效地執行(詳細資訊請參閱第3章和第6章)。例如，在最壞的情況下，在O(r)時間內alldifferent都可以使邊界一致，相比於弧一致性的O(r2d)，其中r是約束的濃度，d是變數域的大小。此外，對於一些問題，可以證明弧一致性所執行的修剪量與邊界一致性所執行的修剪量是相等的，因此不需要償還弧一致性所帶來的額外成本。

4.3.2 Backtracking and Maintaining Strong k-Consistency

Freuder[39,40]定義了一種稱為強k-一致性的區域性一致性級別。如果滿足由賦值集例項化的所有變數的每個約束，那麼賦值集就是一致的。

對於二進位制csp的特殊情況，強2一致性與弧一致性相同，強3一致性也稱為路徑一致性。CSP可以通過反覆檢測並消除所有的不一致性t = {x1 = a1，…,xj−1 = aj−1 } 1≤j < k,t是一致的但不能擴充套件到某些第j個變數xj。刪除不一致或nogood t,約束髮布規則的元組的CSP t。實施強有力的k-consistency可能大大增加的數量限制在CSP,隨著新的約束可以在k指數。一旦一個CSP已經強烈k-consistent任何價值仍在變數的域可以擴充套件到一組一致的作業/ k變數backtrack-free的方式。但是，除非k = n，否則不能保證一個值可以擴充套件到所有n個變數的解。在含有任意約束條件的CSP上執行強k一致性的最優演算法具有O(nkdk)最壞情況時間複雜度，其中n是CSP中的變數數量，d是變數[29]的域大小。

假設MCk是在搜尋過程中保持強k一致性的演算法(見表4.1)。為了指定MCk，我假設分支策略是列舉的，因此，搜尋樹中的每個節點都對應一組賦值。在搜尋過程中，我們希望維護這樣一個屬性，即變數域中的任何值都可以擴充套件到k個變數上的一致賦值集。要做到這一點，我們必須在概念上通過修改約束來考慮當前的賦值集。給定一組賦值t，只選擇約束中與t中的賦值一致的元組，然後將這些元組投影到約束的未例項化變數集上，以給出新的約束(詳細資訊請參見[25])。在這種體系結構下，FC可以看作是保持一種一致性，而對於二進位制csp, MAC可以看作是保持強二一致性。

這樣的架構對於k > 2是否可行?有證據表明答案是肯定的。Van Gelder和Tsuji[127]提出了一種保持二元子句(兩個文字子句)解析度封閉性的演算法，實驗證明該演算法在較大的SAT例項上可以比DPLL快得多。該演算法可以看作是專門針對SAT的MC3演算法。Bacchus[2]在此工作的基礎上，證明了所得到的SAT演算法具有較強的魯棒性，與最先進的DPLL演算法具有競爭力。考慮到已經有大量的工程投入到DPLL的求解中，這一點是值得注意的。然而，到目前為止，雖然已經作出了努力，但還沒有令人信服的證據證明一般的戰略檔案具有相應的結果。