Learn OpenGL (十二):投光物
平行光
當一個光源處於很遠的地方時,來自光源的每條光線就會近似於互相平行。不論物體和/或者觀察者的位置,看起來好像所有的光都來自於同一個方向。當我們使用一個假設光源處於無限遠處的模型時,它就被稱為定向光,因為它的所有光線都有著相同的方向,它與光源的位置是沒有關係的。
定向光非常好的一個例子就是太陽。太陽距離我們並不是無限遠,但它已經遠到在光照計算中可以把它視為無限遠了。所以來自太陽的所有光線將被模擬為平行光線,我們可以在下圖看到:

因為所有的光線都是平行的,所以物體與光源的相對位置是不重要的,因為對場景中每一個物體光的方向都是一致的。由於光的位置向量保持一致,場景中每個物體的光照計算將會是類似的。
我們可以定義一個光線方向向量而不是位置向量來模擬一個定向光。著色器的計算基本保持不變,但這次我們將直接使用光的direction向量而不是通過direction來計算lightDir向量。
struct Light { // vec3 position; // 使用定向光就不再需要了 vec3 direction; vec3 ambient; vec3 diffuse; vec3 specular; }; ... void main() { vec3 lightDir = normalize(-light.direction); ... }
注意我們首先對light.direction向量取反。我們目前使用的光照計算需求一個從片段至光源的光線方向,但人們更習慣定義定向光為一個從光源出發的全域性方向。所以我們需要對全域性光照方向向量取反來改變它的方向,它現在是一個指向光源的方向向量了。而且,記得對向量進行標準化,假設輸入向量為一個單位向量是很不明智的。
最終的lightDir向量將和以前一樣用在漫反射和鏡面光計算中。
為了清楚地展示定向光對多個物體具有相同的影響,我們將會再次使用座標系統章節最後的那個箱子派對的場景。如果你錯過了派對,我們先定義了十個不同的箱子位置,並對每個箱子都生成了一個不同的模型矩陣,每個模型矩陣都包含了對應的區域性-世界座標變換:
for(unsigned int i = 0; i < 10; i++)
{
glm::mat4 model;
model = glm::translate(model, cubePositions[i]);
float angle = 20.0f * i;
model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
lightingShader.setMat4("model", model);
glDrawArrays(GL_TRIANGLES, 0, 36);
}
同時,不要忘記定義光源的方向(注意我們將方向定義為從光源出發的方向,你可以很容易看到光的方向朝下)。
lightingShader.setVec3("light.direction", -0.2f, -1.0f, -0.3f);
如果你現在編譯程式,在場景中自由移動,你就可以看到好像有一個太陽一樣的光源對所有的物體投光。你能注意到漫反射和鏡面光分量的反應都好像在天空中有一個光源的感覺嗎?它會看起來像這樣:
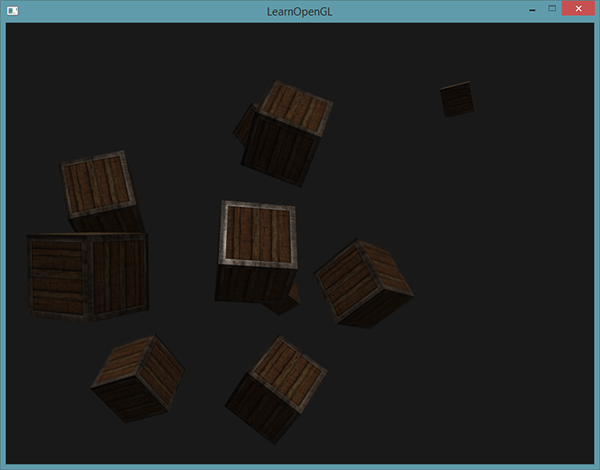
你可以在這裡找到程式的所有程式碼。
點光源
定向光對於照亮整個場景的全域性光源是非常棒的,但除了定向光之外我們也需要一些分散在場景中的點光源(Point Light)。點光源是處於世界中某一個位置的光源,它會朝著所有方向發光,但光線會隨著距離逐漸衰減。想象作為投光物的燈泡和火把,它們都是點光源。
在之前的教程中,我們一直都在使用一個(簡化的)點光源。我們在給定位置有一個光源,它會從它的光源位置開始朝著所有方向散射光線。然而,我們定義的光源模擬的是永遠不會衰減的光線,這看起來像是光源亮度非常的強。在大部分的3D模擬中,我們都希望模擬的光源僅照亮光源附近的區域而不是整個場景。
如果你將10個箱子加入到上一節光照場景中,你會注意到在最後面的箱子和在燈面前的箱子都以相同的強度被照亮,並沒有定義一個公式來將光隨距離衰減。我們希望在後排的箱子與前排的箱子相比僅僅是被輕微地照亮。
衰減
隨著光線傳播距離的增長逐漸削減光的強度通常叫做衰減(Attenuation)。隨距離減少光強度的一種方式是使用一個線性方程。這樣的方程能夠隨著距離的增長線性地減少光的強度,從而讓遠處的物體更暗。然而,這樣的線性方程通常會看起來比較假。在現實世界中,燈在近處通常會非常亮,但隨著距離的增加光源的亮度一開始會下降非常快,但在遠處時剩餘的光強度就會下降的非常緩慢了。所以,我們需要一個不同的公式來減少光的強度。
幸運的是一些聰明的人已經幫我們解決了這個問題。下面這個公式根據片段距光源的距離計算了衰減值,之後我們會將它乘以光的強度向量:

在這裡dd代表了片段距光源的距離。接下來為了計算衰減值,我們定義3個(可配置的)項:常數項KcKc、一次項KlKl和二次項KqKq。
- 常數項通常保持為1.0,它的主要作用是保證分母永遠不會比1小,否則的話在某些距離上它反而會增加強度,這肯定不是我們想要的效果。
- 一次項會與距離值相乘,以線性的方式減少強度。
- 二次項會與距離的平方相乘,讓光源以二次遞減的方式減少強度。二次項在距離比較小的時候影響會比一次項小很多,但當距離值比較大的時候它就會比一次項更大了。
由於二次項的存在,光線會在大部分時候以線性的方式衰退,直到距離變得足夠大,讓二次項超過一次項,光的強度會以更快的速度下降。這樣的結果就是,光在近距離時亮度很高,但隨著距離變遠亮度迅速降低,最後會以更慢的速度減少亮度。下面這張圖顯示了在100的距離內衰減的效果:
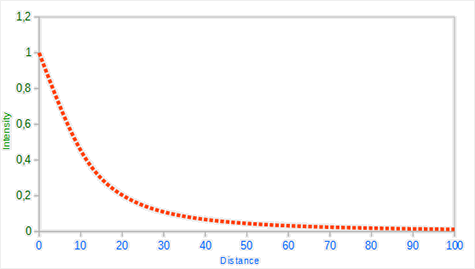
你可以看到光在近距離的時候有著最高的強度,但隨著距離增長,它的強度明顯減弱,並緩慢地在距離大約100的時候強度接近0。這正是我們想要的。
選擇正確的值
但是,該對這三個項設定什麼值呢?正確地設定它們的值取決於很多因素:環境、希望光覆蓋的距離、光的型別等。在大多數情況下,這都是經驗的問題,以及適量的調整。下面這個表格顯示了模擬一個(大概)真實的,覆蓋特定半徑(距離)的光源時,這些項可能取的一些值。第一列指定的是在給定的三項時光所能覆蓋的距離。這些值是大多數光源很好的起始點,它們由Ogre3D的Wiki所提供:
| 距離 | 常數項 | 一次項 | 二次項 |
|---|---|---|---|
| 7 | 1.0 | 0.7 | 1.8 |
| 13 | 1.0 | 0.35 | 0.44 |
| 20 | 1.0 | 0.22 | 0.20 |
| 32 | 1.0 | 0.14 | 0.07 |
| 50 | 1.0 | 0.09 | 0.032 |
| 65 | 1.0 | 0.07 | 0.017 |
| 100 | 1.0 | 0.045 | 0.0075 |
| 160 | 1.0 | 0.027 | 0.0028 |
| 200 | 1.0 | 0.022 | 0.0019 |
| 325 | 1.0 | 0.014 | 0.0007 |
| 600 | 1.0 | 0.007 | 0.0002 |
| 3250 | 1.0 | 0.0014 | 0.000007 |
你可以看到,常數項KcKc在所有的情況下都是1.0。一次項KlKl為了覆蓋更遠的距離通常都很小,二次項KqKq甚至更小。嘗試對這些值進行實驗,看看它們在你的實現中有什麼效果。在我們的環境中,32到100的距離對大多數的光源都足夠了。
實現衰減
為了實現衰減,在片段著色器中我們還需要三個額外的值:也就是公式中的常數項、一次項和二次項。它們最好儲存在之前定義的Light結構體中。注意我們使用上一節中計算lightDir的方法,而不是上面定向光部分的。
struct Light {
vec3 position;
vec3 ambient;
vec3 diffuse;
vec3 specular;
float constant;
float linear;
float quadratic;
};
然後我們將在OpenGL中設定這些項:我們希望光源能夠覆蓋50的距離,所以我們會使用表格中對應的常數項、一次項和二次項:
lightingShader.setFloat("light.constant", 1.0f);
lightingShader.setFloat("light.linear", 0.09f);
lightingShader.setFloat("light.quadratic", 0.032f);
在片段著色器中實現衰減還是比較直接的:我們根據公式計算衰減值,之後再分別乘以環境光、漫反射和鏡面光分量。
我們仍需要公式中距光源的距離,還記得我們是怎麼計算一個向量的長度的嗎?我們可以通過獲取片段和光源之間的向量差,並獲取結果向量的長度作為距離項。我們可以使用GLSL內建的length函式來完成這一點:
float distance = length(light.position - FragPos);
float attenuation = 1.0 / (light.constant + light.linear * distance +
light.quadratic * (distance * distance));
接下來,我們將包含這個衰減值到光照計算中,將它分別乘以環境光、漫反射和鏡面光顏色。
我們可以將環境光分量保持不變,讓環境光照不會隨著距離減少,但是如果我們使用多於一個的光源,所有的環境光分量將會開始疊加,所以在這種情況下我們也希望衰減環境光照。簡單實驗一下,看看什麼才能在你的環境中效果最好。
ambient *= attenuation;
diffuse *= attenuation;
specular *= attenuation;
如果你執行程式的話,你會獲得這樣的結果:
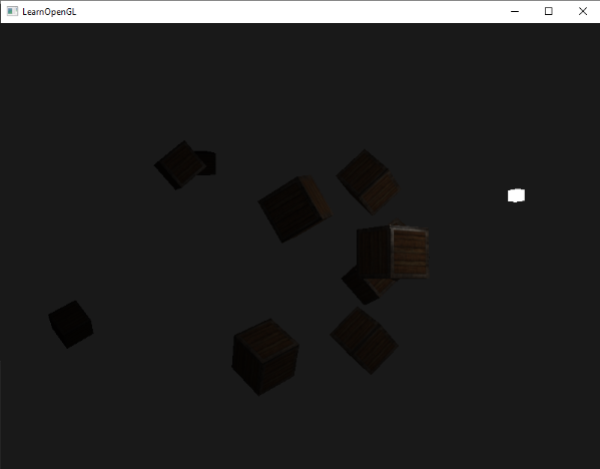
你可以看到,只有前排的箱子被照亮的,距離最近的箱子是最亮的。後排的箱子一點都沒有照亮,因為它們離光源實在是太遠了。你可以在這裡找到程式的程式碼。
點光源就是一個能夠配置位置和衰減的光源。它是我們光照工具箱中的又一個光照型別。
聚光
我們要討論的最後一種型別的光是聚光(Spotlight)。聚光是位於環境中某個位置的光源,它只朝一個特定方向而不是所有方向照射光線。這樣的結果就是隻有在聚光方向的特定半徑內的物體才會被照亮,其它的物體都會保持黑暗。聚光很好的例子就是路燈或手電筒。
OpenGL中聚光是用一個世界空間位置、一個方向和一個切光角(Cutoff Angle)來表示的,切光角指定了聚光的半徑(譯註:是圓錐的半徑不是距光源距離那個半徑)。對於每個片段,我們會計算片段是否位於聚光的切光方向之間(也就是在錐形內),如果是的話,我們就會相應地照亮片段。下面這張圖會讓你明白聚光是如何工作的:
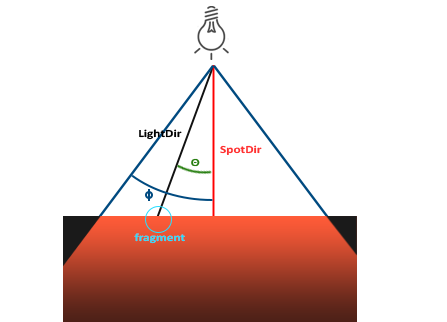
LightDir:從片段指向光源的向量。SpotDir:聚光所指向的方向。Phiϕ:指定了聚光半徑的切光角。落在這個角度之外的物體都不會被這個聚光所照亮。Thetaθ:LightDir向量和SpotDir向量之間的夾角。在聚光內部的話θ值應該比ϕ值小。
所以我們要做的就是計算LightDir向量和SpotDir向量之間的點積(還記得它會返回兩個單位向量夾角的餘弦值嗎?),並將它與切光角ϕ值對比。你現在應該瞭解聚光究竟是什麼了,下面我們將以手電筒的形式建立一個聚光。
手電筒
手電筒(Flashlight)是一個位於觀察者位置的聚光,通常它都會瞄準玩家視角的正前方。基本上說,手電筒就是普通的聚光,但它的位置和方向會隨著玩家的位置和朝向不斷更新。
所以,在片段著色器中我們需要的值有聚光的位置向量(來計算光的方向向量)、聚光的方向向量和一個切光角。我們可以將它們儲存在Light結構體中:
struct Light {
vec3 position;
vec3 direction;
float cutOff;
...
};
接下來我們將合適的值傳到著色器中:
lightingShader.setVec3("light.position", camera.Position);
lightingShader.setVec3("light.direction", camera.Front);
lightingShader.setFloat("light.cutOff", glm::cos(glm::radians(12.5f)));
你可以看到,我們並沒有給切光角設定一個角度值,反而是用角度值計算了一個餘弦值,將餘弦結果傳遞到片段著色器中。這樣做的原因是在片段著色器中,我們會計算LightDir和SpotDir向量的點積,這個點積返回的將是一個餘弦值而不是角度值,所以我們不能直接使用角度值和餘弦值進行比較。為了獲取角度值我們需要計算點積結果的反餘弦,這是一個開銷很大的計算。所以為了節約一點效能開銷,我們將會計算切光角對應的餘弦值,並將它的結果傳入片段著色器中。由於這兩個角度現在都由余弦角來表示了,我們可以直接對它們進行比較而不用進行任何開銷高昂的計算。
接下來就是計算θθ值,並將它和切光角ϕϕ對比,來決定是否在聚光的內部:
float theta = dot(lightDir, normalize(-light.direction));
if(theta > light.cutOff)
{
// 執行光照計算
}
else // 否則,使用環境光,讓場景在聚光之外時不至於完全黑暗
color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0);
我們首先計算了lightDir和取反的direction向量(取反的是因為我們想讓向量指向光源而不是從光源出發)之間的點積。記住要對所有的相關向量標準化。
你可能奇怪為什麼在if條件中使用的是 > 符號而不是 < 符號。theta不應該比光的切光角更小才是在聚光內部嗎?這並沒有錯,但不要忘記角度值現在都由余弦值來表示的。一個0度的角度表示的是1.0的餘弦值,而一個90度的角度表示的是0.0的餘弦值,你可以在下圖中看到:
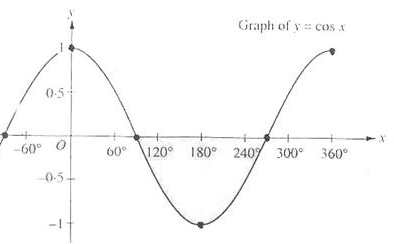
你現在可以看到,餘弦值越接近1.0,它的角度就越小。這也就解釋了為什麼theta要比切光值更大了。切光值目前設定為12.5的餘弦,約等於0.9978,所以在0.9979到1.0內的theta值才能保證片段在聚光內,從而被照亮。
執行程式,你將會看到一個聚光,它僅會照亮聚光圓錐內的片段。看起來像是這樣的:
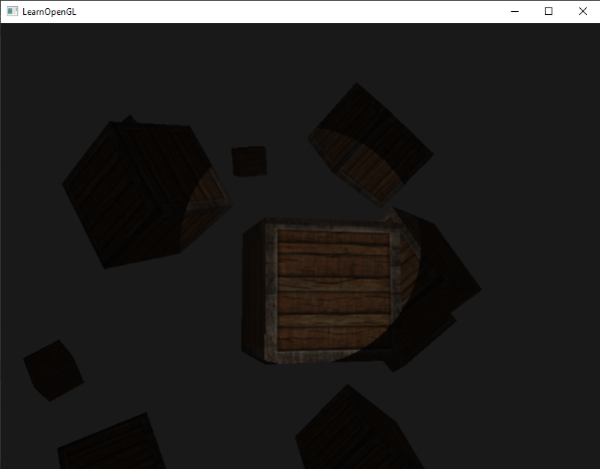
你可以在這裡獲得全部原始碼。
但這仍看起來有些假,主要是因為聚光有一圈硬邊。當一個片段遇到聚光圓錐的邊緣時,它會完全變暗,沒有一點平滑的過渡。一個真實的聚光將會在邊緣處逐漸減少亮度。
平滑/軟化邊緣
為了建立一種看起來邊緣平滑的聚光,我們需要模擬聚光有一個內圓錐(Inner Cone)和一個外圓錐(Outer Cone)。我們可以將內圓錐設定為上一部分中的那個圓錐,但我們也需要一個外圓錐,來讓光從內圓錐逐漸減暗,直到外圓錐的邊界。
為了建立一個外圓錐,我們只需要再定義一個餘弦值來代表聚光方向向量和外圓錐向量(等於它的半徑)的夾角。然後,如果一個片段處於內外圓錐之間,將會給它計算出一個0.0到1.0之間的強度值。如果片段在內圓錐之內,它的強度就是1.0,如果在外圓錐之外強度值就是0.0。
我們可以用下面這個公式來計算這個值:
I=θ−γϵI=θ−γϵ
這裡ϵϵ(Epsilon)是內(ϕϕ)和外圓錐(γγ)之間的餘弦值差(ϵ=ϕ−γϵ=ϕ−γ)。最終的II值就是在當前片段聚光的強度。
很難去表現這個公式是怎麼工作的,所以我們用一些例項值來看看:
| θθ | θθ(角度) | ϕϕ(內光切) | ϕϕ(角度) | γγ(外光切) | γγ(角度) | ϵϵ | II |
|---|---|---|---|---|---|---|---|
| 0.87 | 30 | 0.91 | 25 | 0.82 | 35 | 0.91 - 0.82 = 0.09 | 0.87 - 0.82 / 0.09 = 0.56 |
| 0.9 | 26 | 0.91 | 25 | 0.82 | 35 | 0.91 - 0.82 = 0.09 | 0.9 - 0.82 / 0.09 = 0.89 |
| 0.97 | 14 | 0.91 | 25 | 0.82 | 35 | 0.91 - 0.82 = 0.09 | 0.97 - 0.82 / 0.09 = 1.67 |
| 0.83 | 34 | 0.91 | 25 | 0.82 | 35 | 0.91 - 0.82 = 0.09 | 0.83 - 0.82 / 0.09 = 0.11 |
| 0.64 | 50 | 0.91 | 25 | 0.82 | 35 | 0.91 - 0.82 = 0.09 | 0.64 - 0.82 / 0.09 = -2.0 |
| 0.966 | 15 | 0.9978 | 12.5 | 0.953 | 17.5 | 0.966 - 0.953 = 0.0448 | 0.966 - 0.953 / 0.0448 = 0.29 |
你可以看到,我們基本是在內外餘弦值之間根據θθ插值。如果你仍不明白髮生了什麼,不必擔心,只需要記住這個公式就好了,在你更聰明的時候再回來看看。
我們現在有了一個在聚光外是負的,在內圓錐內大於1.0的,在邊緣處於兩者之間的強度值了。如果我們正確地約束(Clamp)這個值,在片段著色器中就不再需要if-else了,我們能夠使用計算出來的強度值直接乘以光照分量:
float theta = dot(lightDir, normalize(-light.direction));
float epsilon = light.cutOff - light.outerCutOff;
float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0);
...
// 將不對環境光做出影響,讓它總是能有一點光
diffuse *= intensity;
specular *= intensity;
...
注意我們使用了clamp函式,它把第一個引數約束(Clamp)在了0.0到1.0之間。這保證強度值不會在[0, 1]區間之外。
確定你將outerCutOff值新增到了Light結構體之中,並在程式中設定它的uniform值。下面的圖片中,我們使用的內切光角是12.5,外切光角是17.5:
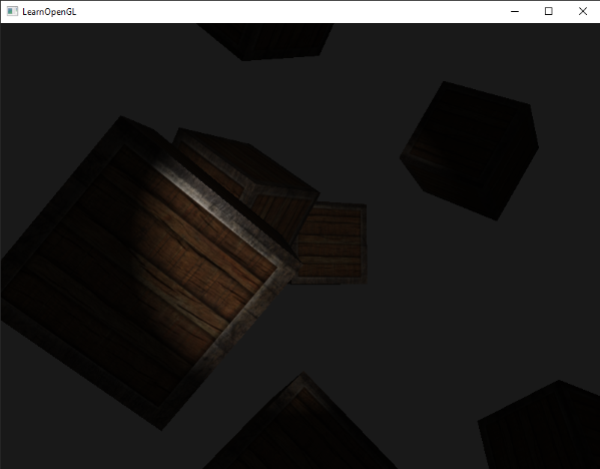
啊,這樣看起來就好多了。稍微對內外切光角實驗一下,嘗試建立一個更能符合你需求的聚光。你可以在這裡找到程式的原始碼。
這樣的手電筒/聚光型別的燈光非常適合恐怖遊戲,結合定向光和點光源,環境就會開始被照亮了。在下一節的教程中,我們將會結合我們至今討論的所有光照和技巧。
