編碼的奧祕：二進位制數
轉自：《編碼的奧祕》 第九章
1 9 7 3年，當安東尼·奧蘭多在他寫的一首歌中要求他摯愛的人“系一條黃色的綢帶在橡樹上”時，他並沒有要求他的愛人進行繁瑣的解釋或冗長的討論，只要求她給他一個簡單的結果。他不去關心其中的因果，即使歌中複雜的感情和動情的歷史在現實生活中重演，所有的人真正想知道的僅僅是一個簡單的是或不是。他希望在樹上系一條黃色的綢帶來表示： “是的，即使你犯了很大的錯，並且被判了入獄三年，我仍希望你回來和我一起共渡時光。 ”他希望用樹上沒有黃色的綢帶來表示： “你連停在這裡都別想。 ”
這是兩個界線分明、相互排斥的答案。奧蘭多沒有這樣唱： “如果你想再考慮一下的話，就係半條黃色的綢帶”或者“如果你不愛我但仍希望我們是朋友，就係一條藍色的綢帶吧”。相反，他讓答案非常的簡單。
和黃色綢帶的有無具有同樣效果的另外幾個例子（但可能無法用在詩裡）是可以選擇一種交通標記放在院外，可能是“請進”或 “此路不通”。
或者在門上掛一個牌子，上寫“關”或“開”。
或者用從視窗能夠看到的一盞燈的亮滅來表示。
如果你只需說“是”或“不是”的話，可以有很多種方式來表達。你不必用一個句子來表達是或不是，也不需要一個單詞，甚至連一個字母都不要。你只要用一個位元，即只要一個0或1 即可。
正如我們在前面的章節中所瞭解到的，通常用來計數的十進位制數事實上並沒有什麼與眾不同的地方。非常清楚，我們的數字系統之所以是基於 1 0的（十進位制數）是因為我們有 1 0個手指頭。我們同樣有理由使用八進位制數字系統（如果我們是卡通人物）或四進位制數字系統（如果我們是龍蝦），甚至是二進位制數字系統（如果我們是海豚）。
但是，二進位制數字系統有一點兒特別：它可能是最簡單的數字系統。二進位制數字系統中只有兩種二進位制數字—0和1 。要是我們想尋求更簡單的數字系統，只好把數字 1 去掉，這樣，就只剩下 0一個數字了。只有一個數字 0的數字系統是什麼都做不成的。
“ b i t (位元)”這個詞被創造出來代表“ binary digit”，它的確是新造的和計算機相關的最可愛的詞之一。當然， “ b i t”有其通常的意義： “一小部分，程度很低或數量很少”。這個意義用來表示位元是非常精確的，因為 1 位元—一個二進位制數字位—確實是一個非常小的量。
有時候當一個新詞誕生時，它還包含了一種新的意思。 b i t這個詞也是這樣。 1 位元的意思超過了被海豚用來數數的二進位制數字位所包含的意義。在計算機時代，位元已經被看作是組成資訊塊的基本單位。
當然，上述說法不一定完全正確，位元並不是傳送資訊的唯一的方式。字母、單詞、摩爾斯碼、布萊葉盲文，十進位制數字都可以用來傳遞資訊。位元傳遞的資訊量很小。 1 位元只具備最少的資訊量，更復雜的資訊需要多位位元來傳遞。 （我們說位元傳遞的資訊量小，並不是說它傳送的資訊不重要。事實上黃綢帶對於與它相關的兩個人來說是一個非常重要的資訊。 ）
“聽，孩子們，你們很快就能聽到 Paul Revere 午夜的馬蹄聲。 ”享利·朗費羅寫道。儘管他在描述 Paul Revere是怎樣通知美國人英國殖民者入侵的訊息時不一定與史實完全一致，但他的確提供了一個利用位元傳遞資訊的令人茅塞頓開的例子：
也就是說， Paul Revere 的朋友有兩盞燈。如果英軍由陸路入侵，他就掛一盞燈在教堂的鐘樓上；如果英軍由海路入侵，他就掛兩盞燈在教堂的鐘樓上。
然而，朗費羅並沒有將所有的可能都涉及到。他留下第三種情況沒有說，那就是英軍根本就沒有入侵的情況。朗費羅已經暗示第三種可能的資訊可以由不掛提燈的方式來傳遞。
讓我們假設那兩盞燈是永久固定在教堂鐘樓上的。在正常情況下，它們都不亮：
這就是指英軍還沒有入侵。如果一盞提燈亮：
表示英軍正由陸路入侵。如果兩盞提燈都亮：
表示英軍正由海路入侵。
每一盞提燈都代表一個位元。亮著的燈表示比持值為 1 ，未亮的燈表示位元值為 0。前面奧蘭多已經說明了傳送只有兩種可能性的資訊只需要一個位元。如果 Paul Revere只需被告知英軍正在入侵（不管是從何處入侵）的訊息，一盞提燈就足夠了。點亮提燈代表英軍入侵，未點亮提燈代表又是一個和平之夜。
傳遞三種可能性的訊息還需要再有一盞提燈。一旦再有一盞提燈，兩個位元就可以通知有四種可能的資訊
Paul Revere 將三種可能性用兩盞提燈來傳送的做法事實上是相當富有經驗的。用通訊理論的術語說，他採用了冗餘的辦法來降低噪聲的影響。通訊理論中的噪聲是指影響通訊效果的任何事物。電話線路中的靜電流顯然是影響電話通訊的一種噪聲。然而，即使是在有噪聲的情況下，電話通訊仍能夠成功，因為口語中存在大量的冗餘。你同樣可以聽懂對方的話而無需將每個音節、每個字都聽得很清楚。
在上述例子中，噪聲是指晚上光線黯淡以及 Paul Revere 距鐘樓有一定的距離，它們都阻礙了 Paul Revere聲將鐘樓上的兩盞燈區分清楚。下面是朗費羅的詩中很重要的一段：
那當然不是說 Paul Revere正在辨清到底是哪盞燈先亮的問題。
這裡最本質的概念是資訊可能代表兩種或多種可能性的一種。例如，當你和別人談話時，說的每個字都是字典中所有字中的一個。如果給字典中所有的字從 1 開始編號，我們就可能精確地使用數字進行交談，而不使用單詞。 （當然，對話的兩個人都需要一本已經給每個字編過號的字典以及足夠的耐心。 ）
換句話說，任何可以轉換成兩種或多種可能的資訊都可以用位元來表示。不用說，人類使用的很多資訊都無法用離散的可能性來表示，但這些資訊對我們人類的生存又是至關重要的。這就是人類無法和計算機建立起浪漫關係的原因所在（無論怎樣，都希望這種情況不會發生） 。如果無法將某些資訊以語言、圖片或聲音的形式表達，那也不可能將這些資訊以位元的形式編碼。當然，你也不會想將它們編碼。
舉手或不舉手是一個位元的資訊。兩個人是否舉手—就像電影評論家 Roger Ebert和剛去世不久的 Gene Siskel對新影片提供他們最終的評價結果那樣—傳遞兩個位元的資訊。 （我們將忽略掉他們實際上對影片做的評語，而只關心他們有沒有舉手的問題。 ）這樣，我們用兩個位元代表四種可能：
第一個位元值代表 S i s k e l的意見， 0表示 S i s k e l討厭這部影片， 1 表示 S i s k e l喜歡這部影片。同樣，第二個位元值代表 E b e r t的意見。
因此，如果你的朋友問你 S i s k e l和E b e r t是怎麼評價《 Impolite Encounter》這部電影的，你不用回答“S i s k e l舉手了， E b e r t沒有舉手”或者“S i s k e l喜歡這部電影， E b e r t不喜歡這部電影”，你可以簡單地回答“麼零”。你的朋友只要知道哪一位代表的是 S i s k e l的意見，哪一位代表的是E b e r t的意見，並且知道值為 1 代表舉手，值為 0代表沒有舉手，你的回答就是可以被人理解的。當然，你和你的朋友都要知道這種程式碼的含義。
我們也可以一開始就宣告值為 1 的位元位表示沒有舉手，值為 0的位元位表示舉手了，這可能有點違反常規。通常我們會認為值為 1 的位元位代表正面的事情，而值為 0的位元位代表相反的一方面，這的確只是一種很隨意的指派。無論怎樣，用此種程式碼的人只要明白 0、 1 分別代表什麼就可以了。
某一位或幾位位元位的集合所代表的意義通常是和上下文相關的。橡樹上的黃綢帶可能只有系綢帶的人和期望看到綢帶的人知道其中的意思，改變綢帶的顏色、系綢帶的樹或系綢帶的日期，綢帶可能會被認為只是一塊毫無意義的破布。同樣，要從 S i s k e l和 E b e r t的手勢中得到有用的資訊，我們至少要知道正在討論的是哪部影片。
如果你儲存了 S i s k e l和E b e r t對一系列影片的評價和投票結果，你就有可能在表示 S i s k e l和E b e r t意見的位元資訊中再增加一位代表你自己的觀點的位元位。增加的第三位使得其代表的資訊可能性增加到 8種：
使用位元來表示資訊的一個額外好處是我們清楚地知道我們解釋了所有的可能性。 我們知道有且僅有 8種可能性，不多也不少。用 3個位元，我們只能從 0數到7，後面再沒有 3位二進位制數了。
在描述 S i s k e l和 E b e r t的位元時，你可能一直在考慮一個嚴重的，並且是令人煩惱的問題—對於Leonard Maltin的Movie &Video Guide怎麼辦呢？別忘了， Leonard Maltin是不採用舉手表決這種形式的，他對電影的評價用的是更傳統的星級系統。
要想知道需多少個 M a l t i n位元，首先要了解一些關於 M a l t i n評分系統的知識。 M a l t i n給電影的評價是 1 ～4顆星，並且中間可以有半顆星。 （僅僅是為了好玩，他實際上不會給電影只評一顆星，取而代之的是給一個 B O M B［炸彈］。 ）這裡總共有七種可能性，也就是說只需要 3個位元位就可以表示一個特定的評價等級了：
你可能會問 111 怎麼辦呢， 111 這個程式碼什麼意義都沒有，它沒有定義。如果二進位制程式碼111 被用來表示 M a l t i n等級，那一定是出現錯誤了。 （這可能是計算機出的錯誤，因為人不會給出這樣的評分。 ）
前面我們曾用兩個位元來代表 S i s k e l和 E b e r t的評價結果，左邊的一位代表 S i s k e l的評價意見，右邊的一位代表 E b e r t的評價意見。在上述 M a l t i n評分系統中，各個位元位都有確定的意義嗎？是的，當然有。將位元編碼的數值加 2再除以 2，就得到了 M a l t i n評分中對應的星的顆數。這樣編碼是由於我們在定義程式碼時遵循了合理性和連貫性，我們也可以下面的這種方式編碼：
只要大家都瞭解程式碼的含義，這種表示就和前述程式碼一樣，都是合理的。
如果M a l t i n遇到了一部連一顆星都不值得給的電影，他就會給它半顆星。他當然有足夠的程式碼來表示半顆星的情況，程式碼會像下面這樣定義：
但是，如果他再遇到連半顆星的級別都不夠的影片並且決定給它沒有星的級別（ ATO M I C B O M B？），他就得再需要一個位元位了，已經沒有 3個位元的程式碼空閒了。
《Entertainment We e k l y》雜誌常常給事物定級，除了電影之外還有電視節目、 C D、書籍、C D - R O M、網路站點等等。等級的範圍從 A +～ F，如果你數一下的話，發現共有 1 3 個等級。這樣，需要四個位元來代表這些等級：
有3個程式碼沒有用到，它們是： 11 0 1 、 111 0和1111，加上後總共是 1 6個程式碼。
只要談到位元，通常是指特定數目的位元位。擁有的位元位數越多，可以傳遞的不同可能性就越多。
對十進位制數當然也是同樣的道理。例如，電話號碼的區號有幾位呢？區號共有 3 位數字。如果所有的區號都使用的話（實際上有一部分割槽號並沒有使用，將它們忽略） ，一共有 1 0^3或1 0 0 0個程式碼，從 0 0 0～ 9 9 9。區號為 2 1 2的 7位數的電話號碼有多少種可能呢？ 1 0^7或10 000 000個；區號為 2 1 2並且以 2 6 0開頭的電話號碼有多少個呢？ 1 0^4或10 000個。
同樣，在二進位制數中，可能的程式碼數等於 2的位元位數次冪：
每增加一個位元位，二進位制程式碼數翻一番。
如果知道需要多少個程式碼，那麼怎樣才能知道需要多少個位元位呢？換句話說，在上述表中，如何才能由程式碼數反推出位元位數呢？
用到的方法叫作取以 2為底的對數，對數運算是冪運算的逆運算。我們知道 2的7次冪等於1 2 8，以 2為底的 1 2 8的對數就等於 7。用數學記號來表示第一個句子為： 
它與下述句子等價：
因此，如果以 2為底的 1 2 8 的對數等於 7，以 2為底的 2 5 6的對數等於 8，那麼，以 2為底的2 0 0的對數等於多少呢？大約是 7 . 6 4，但實際上並不需要知道它。如果要表示 2 0 0種不同的事物，我們共需要 8個位元。
位元通常無法從日常觀察中找到，它深藏於電子裝置中。我們看不到壓縮磁碟 ( C D )、數字手錶或計算機中編過碼的位元，但有時候位元也可以清晰地看到。
下面就是一個例子。如果你手頭有一個使用 3 5毫米膠片的相機，觀察一下它的卷軸。這樣拿住膠捲：
膠捲上有像國際跳棋棋盤一樣的銀色和黑色方格，方格已用數字 1 ～ 1 2標識。這叫作 D X編碼，這 1 2個方格實際上是 1 2個位元。一個銀色的方格代表值為 1 的位元，一個黑色的方格代表值為 0的位元。方格 1 和7通常是銀色的（代表 1 ）。
這些位元是什麼意思呢？你可能知道有些膠片對光的敏感程度要比其他膠片強，這種對光的敏感程度稱作 膠片速度 。說對光非常敏感的膠片很快是因為這種膠片的曝光速度快。曝光速度是由 A S A（ American standards association，美國標準協會）來制定等級的，最常用的等級有 1 0 0、 2 0 0和4 0 0。 A S A等級不只是以十進位制數字的形式印在膠捲的外包裝和暗盒上，而
且還以位元的形式進行了編碼。
膠捲總共有 2 4個A S A等級，它們是：
為A S A等級編碼需要多少個位元呢？答案是 5個位元。我們知道， 2 4= 1 6，與 2 4比太小了；2 5 = 32 ，又超過了所需的編碼數。
位元值與膠片速度的對應關係如下所示：
多數現代的 3 5毫米照相機膠片用的都是這些程式碼（除了那些要手工進行曝光的相機和具有內建式測光表但需要手工設定曝光速度的相機以外）。如果你看過照相機的內部放置膠捲的地方，你應該能夠看到和膠片的金屬方格（ 1 ～6號）相對應的 6個金屬可接觸點。銀色方格實際上是膠捲暗盒中的金屬，是導體；油漆了的黑色方格，是絕緣體。
照相機的電子線路中有一支流向方格 1 的電流，方格 1 通常是銀色的。這支電流有可能流到方格 2～ 6，這要依方格中是純銀還是塗了油漆而定。這樣，如果照相機在接觸點 4和 5檢測到了電流而在接觸點 2、 3 和6沒有檢測到，膠片的速度就是 4 0 0 A S A。照相機可以據此調節曝光時間。
廉價的照相機只要讀方格 2和方格 3，並且假定膠片速度是 5 0、 1 0 0、 2 0 0或4 0 0 A S A四種可能速度之一。
多數相機不讀方格 8～1 2。方格 8、 9、 1 0用來對這卷膠捲進行編碼；方格 11 和1 2指出曝光範圍，依膠片用於黑白照片、彩色照片還是幻燈片而定。
也許最常見的二進位制數的表現形式是無處不在的 U P C（ universal product code，通用產品程式碼） ，即日常所購買的幾乎所有商品包裝上的條形碼。條形碼已經成為計算機在日常生活中應用的一種標誌。
儘管 U P C常常使人多疑，但它確實是一個無辜的小東西，發明出來僅僅是為了實現零售業的結算和存貨管理的自動化，且其應用是相當成功的。當它和一個設計精良的結算系統共同使用時，顧客可以拿到列出細目的售貨憑條，這一點是傳統現金出納員所無法做到的。
有趣的是， U P C也是二進位制程式碼，儘管它初看起來並不像。將 U P C解碼並看看 U P C碼具體是怎樣工作的是很有益的。
通常情況下， U P C是3 0條不同寬度的垂直黑色條紋的集合，由不同寬度的間隙分割開，其下標有一些數字。例如，以下是 C a m p b e l l公司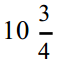 
盎司的罐裝雞汁麵包裝上的 U P C：
可將條形碼形象地看成是細條和黑條，窄間隙和寬間隙的排列形式，事實上，這是觀察條形碼的一種方式。黑色條有四種不同的寬度，較寬的條的寬度是最細條的寬度的兩倍、三倍或者四倍。同樣，各條之間的間隙中較寬的間隙是最窄間隙的兩倍、三倍或者四倍。
但是，看待 U P C的另一種方式是將它看作是一系列的位元。記住，整個條形碼與條形碼掃描器在結算臺“看”到的並不完全一樣。掃描器不會識別條形碼底部的數字，因為識別數字需要一種更復雜的技術—光學字元識別技術，又稱作 O C R（ optical character recognition ）。實際上，掃描器只識別整個條形碼的一條窄帶，條形碼做得很大是為了便於結算臺的操作人員用掃描器對準顧客選購的物品。掃描器所看到的那一條窄帶可以這樣表示：
它看上去是不是很像摩爾斯編碼 ?
當計算機自左向右進行掃描時，它給自己遇到的第一個條分配一個值為 1 的位元值，給與條相鄰的間隙分配一個值為 0的位元值。後續的間隙和條被當作一行中一系列位元中的 1 個、 2個、 3 個還是 4個位元讀進計算機要依據條或間隙的寬度而定。掃描進來的條形碼的位元形式很簡單：
因此，整個U P C只是簡單的由9 5個位元構成的一串。本例中，這些位元可以像下面這樣分組：
起初的 3 個位元通常是 1 0 1 ，這就是最左邊的護線，它幫助計算機掃描器定位。從護線中，掃描器可以知道代表單個位元的條或間隙的寬度，否則，所有包裝上的 U P C印刷大小都是一樣的。
緊挨著最左邊的護線是每組有 7個位元位的六組位元串，每一組是數字 0～9的編碼之一，我們在後面將證明這一點。接著的是 5個位元的中間護線，此固定模式（總是 0 1 0 1 0）是一種內建式的檢錯碼。如果掃描器在應當找到中間護線的地方沒有找到它，掃描器就認為那不是U P C。中間護線是防止條形碼被竄改或錯印的方法之一。
中間護線的後面仍是每組 7個位元的 6組位元串。最後是最右邊的護線，也總是 1 0 1 。最後的最右護線使得 U P C反向掃描（也就是自右向左掃描）同正向掃描一樣成為可能，這一點我們將在後面解釋。
因而整個 U P C對1 2個數字進行了編碼。左邊的 U P C包含了 6個數字的編碼，每個數字佔有7個位元位。你可以用下表進行解碼：
注意，每個 7位程式碼都是以 0開頭，以 1 結尾的。如果掃描器遇到了第一個位元位值為 1 或最後一個位元位值為 0的情況，它就知道自己沒有將 U P C正確地讀入或者是條形碼被竄改了。另外我們還注意到每個程式碼都僅有兩組連續的值為 1 的位元位，這就意味著每個數字對應著條形碼中的兩個豎條。
上表中的每個程式碼中都包含有奇數個值為 1 的位元位，這也是用於檢測差錯和資料一致性的一種機制，稱為奇偶校驗。如果一組位元位中含有奇數個 1 ，就稱之為奇校驗；如果含有偶數個1 ，就稱之為偶校驗。這樣看來，所有這些程式碼都擁有奇校驗。
為了給U P S右邊的 7位一組的數字解碼，可以採用下面的表格：
這些程式碼都是前述程式碼的補碼或補數：凡是 1 的地方都換成 0，凡是 0的地方都換成 1 。這些程式碼都是以 1 開始，以零結束，並且每組都有偶數個 1 ，稱之為偶校驗。
現在，可以對 U C P進行解碼了。藉助前兩個表格， C a m p b e l l公司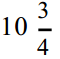 
盎司的罐裝雞汁面的包裝上用 U P C編碼的 1 2個數字是：
0 51000 01251 7
這個結果是令人失望的，正如你所看到的那樣，它們和印在 U P C底部的數字完全相同。（這樣做是有意義的，因為由於某種原因，掃描器可能無法識別條形碼，收銀員就可以手工將這些數字輸進去。 ）我們還沒有完成解碼的全部任務，而且，我們也無法從中解碼任何祕密資訊。然而，關於 U P C的解碼工作已經沒有了，那 3 0個豎條已經變成了 1 2個數字。
第一個數字（在這裡是 0）被稱為數字系統字元， 0的意思是說這是一個規範的 U P C編碼。如果是具有不同重量的貨物的 U P C（像肉類或其他商品） ，這個數字是 2；訂單、票券的 U P C編碼的第一個數字通常是 5。
緊接著的 5 個數字是製造商程式碼。在上例中， 5 1 0 0 0是 Campbell 雞汁面公司的程式碼。C a m p b e l l公司生產的所有產品都使用這個程式碼。再後面的 5個數字（ 0 1 2 5 1 ）是該公司的某種產品的編號，上例中是指 1 0 盎司的罐裝雞汁面。別的公司的雞汁面可能有不同的編號，且0 1 2 5 1 在另外一個公司可能是指一種完全不同的產品。
和通常的想法相反， U P C中沒有包含該種產品的價格。產品的價格資訊可以從商店中使用的與該掃描器相聯的計算機中檢索互到。
最後的數字（這裡是 7）稱作模校驗字元，這個字元可用來進行另外一種錯誤檢驗。為了解釋校驗字元是怎樣工作的，將前 11 個數字（是 0 51000 01251 ）各用一個字母來代替：
然後，計算下式的值：
從緊挨它並大於等於它的一個1 0的整倍數中減去它，其結果稱為模校驗字元。在上例中，有：
緊挨2 3並大於等於 2 3的一個1 0的整倍數是 3 0 ,故：
這就是印在外包裝上並以 U P C形式編碼的模校驗字元，這是一種冗餘措施。如果掃描器計算出來的模校驗結果和 U P C中編碼中的校驗字不一致，計算機就不能將這個 U P C作為一個有效值接收。
正常情況下，表示從 0～9的十進位制數字只需 4個位元就足夠了。在 U P C中，每個數字用了7個位元，這樣總共有 9 5個位元來表示 11 個有用的十進位制數字。事實上， U P C中還包括空白位置（相當於 9個0位元） ，位於左、右護線的兩側。因而，總共有 11 3個位元用來編碼 11 個十進位制數，平均每個十進位制數所用超過了 1 0個位元位！
正像我們所知道的那樣，有部分冗餘對於檢錯來講是必要的。這種商品編碼如果能夠很容易地被顧客用粗頭筆修改的話，這種程式碼措施也就難以發揮其作用了。
U P C編碼可以從兩個方向讀，這一點是非常有益的。如果掃描器解碼的第一個數字是偶校驗（即：每 7位編碼中共有偶數個 1 ），掃描器就知道它正在從右向左進行解碼。計算機系統用下表對右邊的數字解碼：
下面是對左邊數字的解碼錶：
這些 7位編碼與掃描器由左向右掃描時所讀到的編碼完全不同，但不會有模稜兩可的現象。
讓我們再看看本書中提到的由點、劃組成其間用空格分開的摩爾斯電碼。摩爾斯電碼看上去不像是由 0和1 組成的，但它確實是。
下面回憶一下摩爾斯電碼的編碼規則：劃的長度等於點長度的三倍；單個的點或劃之間用長度與點的長度相等的空格分開；單詞內的各個字母之間用長度等於劃的長度的空格分隔；各單詞之間由長度等於兩倍的劃長度的空格分開。
為使分析更加簡單，我們假設劃的長度是點長度的兩倍而不是 3倍。也就是說，一個點是一個值為 1 的位元位，一個劃是兩個值為 1 的位元位，空格是值為 0的位元位。
下面是第 2章的摩爾斯電碼的基本表：
下面是將它轉化為位元形式的結果：
注意，所有的編碼都以 1 開頭，以兩個 0結束。結尾處的兩個零代表單詞中各個字母之間的空格，單詞之間的空格用另外的一對 0來表示。因而， “ H i , t h e r e”的摩爾斯電碼通常是這樣的：
但是，採用位元形式的摩爾斯電碼看起來像 U P C編碼的橫切面：
用位元的形式表示布萊葉盲文比表示摩爾斯電碼容易得多。布萊葉編碼是 6位元程式碼。布萊葉盲文中的每一個字母都是由 6個點組成的，點可能是凸起的，或沒有凸起 (平滑 )的。如在第3章中講的那樣，這些點通常用數字 1 ～6編號：
例如，單詞“ c o d e”可以用布萊葉盲文這樣表示：
如果突起的點是 1 ，平坦的點是 0，則布萊葉盲文中的每一個符號都可以用 6個位元的二進位制程式碼表示。單詞“ c o d e”中的四個布萊葉字母符號就可以簡單地寫成：
最左邊的一位對應編號為 1 的位置，最右邊的一位對應編碼為 6的位置。
正如前面所講到的，位元可以代表單詞、圖片、聲音、音樂、電影，也可以代表產品編碼、膠片速度、電影的受歡迎程度、英軍的入侵以及某人所摯愛的人的意願。但是，最基本的一點是：位元是數字。當用位元表示資訊時只要將可能情況的數目數清楚就可以了，這樣就決定了需要多少個位元位，從而使得各種可能的情況都能分配到一個編號。
位元在哲學和數學的奇怪混合物—邏輯—中發揮作用。邏輯最基本的目標是證明某個語句是否正確，正確與否也可以用 1 和0來表示。