實驗 4:樹和二叉樹的實驗 1
一、實驗目的
1、 熟練理解樹和二叉樹的相關概念,掌握的儲存結構和相關操作實現;
2、 掌握樹的順序結構的實現;
3、 學會運用樹的知識解決實際問題。
二、實驗內容
自己確定一個二叉樹(樹結點型別、數目和結構自定)利用順序結構方法儲存。
實現樹的構造,並完成:
1) 層序輸出結點資料;
2) 以合理的格式,輸出各個結點和雙親、孩子結點資訊;
3) 輸出所有的葉子結點資訊;
4) 分析你的演算法對於給定的二叉樹的儲存效率。
三、設計與編碼
1.本實驗用到的知識理論
(1)二叉樹的順序儲存結構就是一維陣列儲存二叉樹的結點,並且用結點的儲存位置(下標)表示結點之間的邏輯關係;
(2)把二叉樹補充為完全二叉樹再放到陣列中更方便儲存,這樣就可以根據結點之間的邏輯關係可通過下標輸出;
(3)將二叉樹中的結點以編號順序儲存到一維陣列中,注意陣列下標從0快開始。
2.演算法設計
(1)定義BiTree類模板
class BiTree
{
int node[MaxLength]; //用陣列存放資料
int length; //記錄二叉樹大小
public:
BiTree(int *bTree,int n); //建構函式把二叉樹的放到陣列中
~BiTree(){} //解構函式
void OutPut(int length);
void Leaf(); //輸出葉子資訊
};
(2)建構函式:把二叉樹bTree存放到node陣列中,若二叉數某個結點沒有(即0),存放到陣列中就為空,並考慮陣列為滿為空的情況;
(3)層序遍歷:若陣列中某個位置為NULL,則不輸出這個結點;
(4)輸出結點的雙親和孩子結點資訊:通過陣列下標輸出雙親和孩子結點(若沒有,則輸出無雙親、無孩子結點),若結點不存在就跳到下一個;
(5)輸出葉子資訊:
a.不是最後一層但為葉子滿足:既沒有左孩子和右孩子,且該結點不為空
b.在最後一層沒有左孩子且該結點不為空。
3.程式碼
#include<iostream.h>
#define MaxLength 20 //陣列長度為20class BiTree
{
int node[MaxLength]; //用陣列存放資料
int length; //記錄二叉樹大小
public:
BiTree(int *bTree,int n); //建構函式把二叉樹的放到陣列中
~BiTree(){} //解構函式
void Leveroder(); //層序遍歷函式實現
void OutPut(int length);
void Leaf(); //輸出葉子資訊
};
BiTree::BiTree(int *bTree,int n)
{
if(n>=MaxLength||n<1)throw"陣列已滿!||已空!";//判斷陣列是否為滿或空
for(int i=0;i<n;i++)
{
if(bTree[i]==0) //把二叉數中的值放到陣列中
node[i]=NULL;
else node[i]=bTree[i];
}
length=n;
}
void BiTree::Leveroder() //層序遍歷函式實現
{
for(int i=0;i<length;i++)
{
if(node[i]!=NULL) //為NULL(虛結點)時,表示無資料
cout<<node[i]<<" "; //結點不為虛結點標識時依次輸出資料
}
}
void BiTree::OutPut(int length)//輸出結點的雙親和孩子結點資訊
{
for(int j=1;j<length;j++)
{
if(node[j]==NULL) //此時陣列中的值為空,說明在二叉數中沒結點
{
cout<<"第"<<j<<"個結點不存在!"<<endl;
continue;
}
else cout<<"第"<<j<<"個結點值:"<<node[j]<<"\t";
if(node[j/2]==NULL) //此時陣列中的值為空,說明在二叉數中沒雙親
cout<<"無雙親!"<<"\t";
else cout<<"雙親:"<<node[j/2]<<"\t";
if(node[2*j]==NULL||(2*j)>=length) //此時陣列中的值為空,說明在二叉數中沒左孩子
cout<<"無左孩子!"<<"\t";
else cout<<"左孩子:"<<node[2*j]<<"\t";
if(node[2*j+1]==NULL||(2*j+1)>=length) //此時陣列中的值為空,說明在二叉數中沒右孩子
cout<<"無右孩子!"<<endl;
else cout<<"右孩子:"<<node[2*j+1]<<endl;
}
}
void BiTree::Leaf() //輸出葉子資訊
{
int node1,node2;
for(int i=1;i<=length;i++)
{
node1=2*i;
node2=2*i+1;
if(node[node1]==NULL&&node[node2]==NULL&&node[i]!=NULL) //不是最後一層即葉子滿足:既沒有左孩子和右孩子,且該結點不為空
cout<<node[i-1]<<" ";
if(node1>length&&node[i-1]!=NULL) //或者在最後一層沒有左孩子且該結點不為空
cout<<node[i-1]<<" ";
}
}
int main()
{
int bTree[12]={0,8,6,1,25,36,94,0,13,26,0,40}; //非完全二叉數
BiTree node(bTree,12);
cout<<"層序輸出結點資料為:"<<endl;
node.Leveroder();
cout<<endl;
node.OutPut(12);
cout<<endl;
cout<<"葉子結點:"<<endl;
node.Leaf();
cout<<endl;
return 0;
}
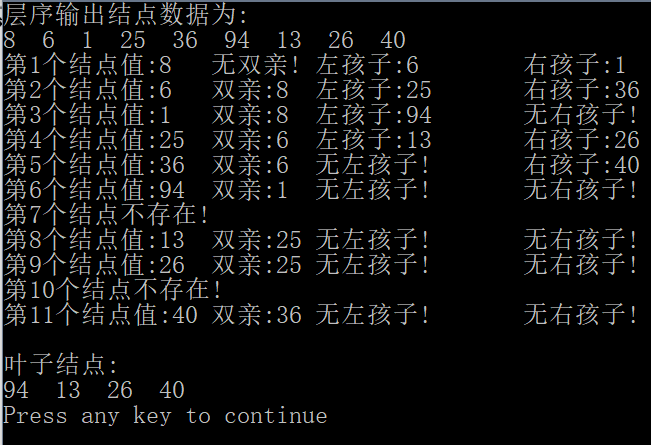
四、執行與測試
五、總結與心得
二叉樹是度不超過2的樹,採用順序儲存的方法,可以將二叉樹補充為完全二叉樹的規格來儲存資料,這種儲存方法適用於完全二叉樹和滿二叉樹,儲存效率較高,但不適用於左斜樹和右斜樹,因為會導致大量儲存空間浪費。