(文章大部分內容摘抄自 結城浩–程式設計師的數學)

很推薦大家閱讀此本書,作者對程式設計師涉及的數學知識的觀點非常新穎,而且上面的知識對初學程式的大家非常好消化

課前對話:

GNU是什麼的縮寫?
是GNU is Not Unix的縮寫.
那第一個單詞GNU是什麼的縮寫呢?
…
沒有個頭啊
其實GNU就包含了全部

學習內容

通過漢諾塔謎題讓大家對遞迴有一個初步印象
以階乘,斐波那契數列,帕斯卡三角形為例,學習遞迴和遞推公式
以遞迴形式描畫遞迴圖形的分形圖

**

漢諾塔

**
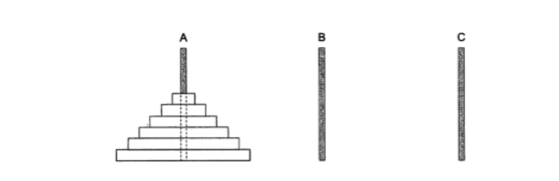
題目:有A,B,C三根細柱,A柱套著6個圓盤,這些圓盤大小各異,按從大到小的順序自下而上擺放

1. 一次只能移動柱子最上端的一個圓盤
2. 小圓盤上不能放大圓盤小圓盤上不能放大圓盤
3. 將1個圓盤從一根柱子移到另一根柱子,算移動1次,那麼,將6個圓盤全部從A移到B最少需要移動幾次呢?
4. 將1個圓盤從一根柱子移到另一根柱子,算移動1次,那麼,將6個圓盤全部從A移到B最少需要移動幾次呢?

將1個圓盤從一根柱子移到另一根柱子,算移動1次,那麼,將6個圓盤全部從A移到B最少需要移動幾次呢?

解決措施:

讓我們先從三個漢諾塔開始解決吧!
(大家可以先把圖蓋住,好好在頭腦裡思考下怎麼移動)

思考題答案:
'6層漢諾塔’可以通過以下步驟求出:

1. 首先,將5個圓盤從A柱移到C柱(解出5層漢諾塔)
2. 然後,將6個之中最大的圓盤從A柱移到B柱
3. 最後,將5個圓盤從C柱移到B柱(解出5層漢諾塔)

‘5層漢諾塔’,‘3層漢諾塔’…也是同樣的解法,'1層漢諾塔’只要移動1次圓盤就OK啦

解出n層漢諾塔的步驟:

1. 當n=0時,
   不用做任何動作
2. 當n>0時

首先,將n-1個圓盤從A柱,經由B柱中轉,移到C柱(解出n-1)層漢諾塔
然後,將1個圓盤從A柱移到B柱
最後,將n-1盤從C柱,經由A柱中轉,移到B柱(解出n-1層漢諾塔)

推出遞推公式

求出解析式

解析式:使用n表示H(n)的式子

廢話少說,放碼過來(Python):

count=0
def hanoi(n,src,dst,mid):     #src:A柱子  dst:B柱  mid:C柱
	global count
	if n==1:  #當前柱子圓盤個數
		print("{}:{}->{}".format(1,src,dst))  #當前柱子只剩下一個圓盤,直接移動
		count+=1
	else:
		hanoi(n-1,src,mid,dst)
		#n-1層的從A柱移動到B柱(中轉站),從B柱移動到C柱
		#n-1層的從C柱移動到A柱(中轉站),從A柱移動到B柱
		print("{}:{}->{}".format(n,src,dst))	#我們命名A柱上的圓盤的編號從上到下為1,2,3
		count+=1
		hanoi(n-1,mid,dst,src)
hanoi(6,'A','B','C')
print(count)

遞迴的思維方式

將複雜問題轉換為較為簡單的同類問題裡是引用