一.核函式

  它是針對線性可分情況進行分析，對於線性不可分的情況，通過使用非線性對映演算法將低維輸入空間線性不可分的樣本轉化為高維特徵空間使其線性可分，從而使得高維特徵空間採用線性演算法對樣本的非線性特徵進行線性分析成為可能。

  它基於結構風險最小化理論之上在特徵空間中構建最優超平面，使得學習器得到全域性最優化，並且在整個樣本空間的期望以某個概率滿足一定上界。

假設X是輸入空間，H是特徵空間，存在一個對映ϕ使得X中的點x能夠計算得到H空間中的點h 

h=ϕ(x) 對於所有的X中的點都成立，x，z是X空間中的點。函式k(x,z)滿足條件： 

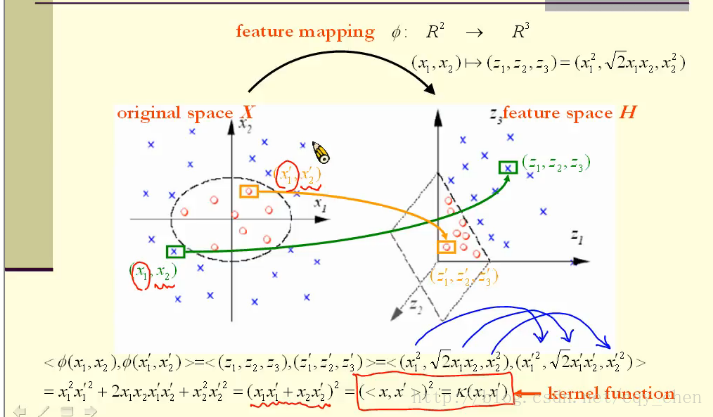
k(x,z)=ϕ(x)⋅ϕ(z) 都成立，則稱k為核函式，而ϕ為對映函式。  舉個例子，如下圖所示： 

特徵空間在三維空間中，原空間在二維，我們定義對映函式為,x=(x1,x2)

那麼如圖所示：  原始空間的點x到特徵空間的點為: 

同時我們可以驗證， ϕ(x)⋅ϕ(z)=k(x,z),

如果我們取 

我們要進行高維空間的線性可分，首先要將原始空間的點通過函式ϕ對映到特徵空間中，然後學習，而所謂的學習，其實就是要計算高維空間的點的距離和夾角。那麼能不能不通過對映函式而直接使用核函式計算高維空間的點的距離以及夾角呢？  答案是可以的，核函式的技巧就是不顯示的定義對映函式，而在高維空間中直接使用核函式進行計算。 

二.核函式的特徵：

核函式必須是連續的，對稱的，並且最優選地應該具有正（半）定Gram矩陣。

三 核函式的基本類別：

3.1 線性核

  由內積<x，y>加上可選的常數c給出。

  表示式 ：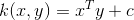

3.2 多項式核函式

表示式：k（x，y）=（αx ^ T y + c）^ d

可調引數是斜率α，常數項c和多項式度d。

3.3 高斯核

高斯核是徑向基函式核的一個例子。

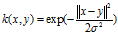
或者，它也可以使用來實現

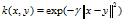
可調引數sigma在核心的效能中起著主要作用，並且應該仔細地調整到手頭的問題。 如果過高估計，指數將幾乎呈線性，高維投影將開始失去其非線性功率。 另一方面，如果低估，該函式將缺乏正則化，並且決策邊界將對訓練資料中的噪聲高度敏感。

3.4指數的核心

指數核與高斯核密切相關，只有正態的平方被忽略。 它也是一個徑向基函式核心。

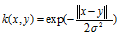
2.5 拉普拉斯運算元核

拉普拉斯核心完全等同於指數核心，除了對sigma引數的變化不那麼敏感。 作為等價的，它也是一個徑向基函式核心。

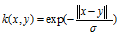
重要的是注意，關於高斯核心的σ引數的觀察也適用於指數和拉普拉斯核心。