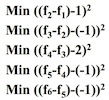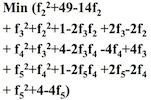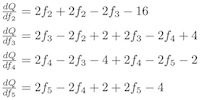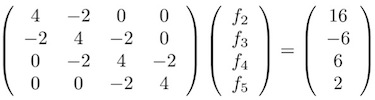Poisson Blending 實現了非常棒的效果，可以看 《自己動手，實現“你的名字”濾鏡》 http://www.cnblogs.com/jsxyhelu/p/7216795.html

它的原理在論文《Poisson Image Editing》中進行了比較詳細的闡述，但是英文的大論文看起來的卻比較麻煩，在 https://wenku.baidu.com/view/55ac10a7be1e650e53ea9990.html 找到一篇《方軼智_基於泊松方程的影象處理 》，這篇成果中，基本把原論文中關於Poisson Blending(泊松融合）的部分翻譯了出來，並且它的綜述部分寫的相當不錯；在

我在自己將這些資料進行歸攏，梳理，並提出自己的思考。首先對幾位作者的辛勤工作表示感謝，資料的版權屬於它們。

一、Poisson Blending(泊松融合）為什麼能夠產生如此好的效果

           它的基本原理基於人的生物學特性。我們人眼天生就對“突變”更為敏感：比如白紙上的黑線；但是如果這個變化是連續平滑的，那麼對人的刺激就要低得多。經過心理學家和電腦科學家的研究，認為二階偏導數對於解決這個方面的融合問題有幫助，所以才有了我們這裡的具體實現。

           影象編輯包括全域性變化和區域性變化，我們關心的是我們所選中的區域性區域中如何幾乎無縫且無影響地嵌入到目標影象中。傳統的工具來完成區域性的剪下，是通過克隆工具直接取代那部分割槽域的內容，因此選擇的片區域的改變會導致明顯的邊縫。所以為了達到我們想要的理想效果，就迫切地需要一種可以消除邊縫的且不改變影象其他特徵的方法。

            這種無縫編輯和克隆方法的核心是數學工具―泊松方程，需滿足在所選區域未知函式的拉普拉斯條件，和它的Dirichlct邊界條件：未知函式的邊界值與目標影象中所選區域的邊界值相同。在這兩個條件下方程的解是唯一的。首先，心理學家Land和Mccan。在1971年提出通過拉普拉斯運算元的限制可以減緩漸變的梯度，當把一幅影象混淆到另一幅影象上幾乎注意不到有什麼影響。並且，泊松方程可以完成無縫地填滿目標影象中的選中區域。

          注意，這裡的脈絡是

          1、“提出需要解決的問題” --> 解決無縫融合；

          2、“解決問題的方法”-->使用Poisson Blending

          3、為什麼-->理解並證明Poisson Blending的特性

二、什麼是泊松方程，以及它在影象處理這裡的運用

         粘點百科：

        泊松方程為[2] 

在這裡 

 代表的是拉普拉斯運算元，而f和 

 可以是在流形上的實數或複數值的方程。當流形屬於歐幾里得空間，而拉普拉斯運算元通常表示為 

 ，因此泊松方程通常寫成

在三維直角座標系，可以寫成

如果有 

 恆等於0，這個方程就會變成一個齊次方程，這個方程稱作“拉普拉斯方程”。

注意，我們影象處理，一般來說，都是屬於歐幾里得空間（而不是黎曼幾何空間），也是在三維之間座標系（而不是極座標系）中的。

在這不多的幾行字裡面，一再提到了“拉普拉斯方程”。實際上，拉普拉斯方程是泊松方程的齊次表達方式。幸好的是，對於拉普拉斯方程我們要熟悉的多，甚至基本知道它的實現方式。

三、主要演算法流程

這裡的三幅圖片分別對應於”前景“”背景“和結果。在原論文中，直接將前景叫做“引導向量域”（我這樣理解，使用前景來引導背景的向量）

符號的含義：設影象定義域S為R^2上封閉子集合，是S的一個封閉子集，它的邊界為。令f*為定義在S上一個已知的標量函式，代表S減去的範圍，令f為定義在上一個未知的標量函式。最終，令v為定義在上的向量域。

定義在上f*的最簡單的插值函式f：最小化問題的插值（在邊界是未知等於已知，在內部是梯度變化最小。梯度在二階偏導為0的時候取極值）

        (1)

        其中

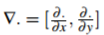        是梯度運算。最小值必須滿足相關的拉格朗日方程。

        (2)

         其中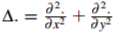是拉普拉斯運算元。

         一個引導域是最小化問題(1)的擴充套件版本中使用的向量域v：（注意 v 是引導向量，也就是前景）

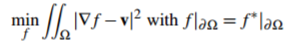        (3)

        它的解是Dirichlet邊界條件下泊松方程的唯一解：

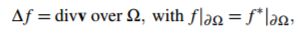        (4)

         其中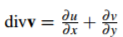是v= （u,v)的散度。

         一個有用的替代方案是理解泊松插值所做的是定義上修正的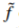函式，以保證。

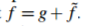       泊松方程(4)隨之成為了以下有邊界條件的拉普拉斯方程：

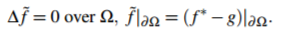       (5)

       因此，在內，我們新增的修正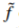是就是邊界上源和目標錯誤匹配(f*-g)的一個插值(membrance interpolant)。這一引導插值的特例被用於無縫克隆。

四、簡單的例子證明

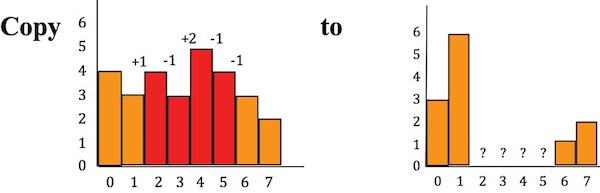
1-D EXAMPLE 一維的例子，這個可以自己上手計算跟著看，效果非常好

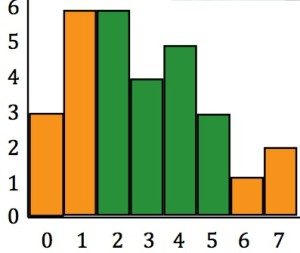
左邊是原圖，相當於前景，紅色直方圖就是引導向量。右邊是背景圖。想把左邊紅色部分移過去，但是又要變化最小，怎麼辦？那麼就是計算

    With   f1 = 6, f6 = 1.

因為這些都是正數，也就相當於計算：

分開求偏導數

變化為矩陣

結論是：

f2 = 6, f3 = 4, f4 = 5, f5 = 3

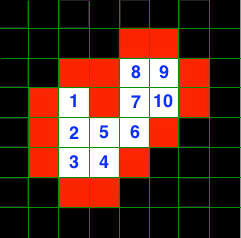
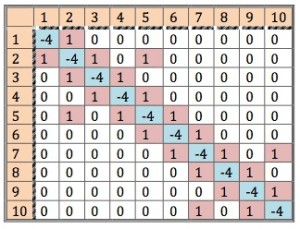
2-D EXAMPLE

可以直接使用簡化的方式，也就是拉普拉斯運算元，進行卷積運算。

六、小結

現在看起來，Poisson Blending的卻是很神奇的。固然它的理論還是比較複雜的，但是也只是在偏導數相關，並且最終可以簡化為拉普拉斯。而我們更幸運，OpenCV中已經對其進行了不錯的封裝，我們可以直接呼叫！然而，對於原理的理解和思考，對於我們儲備基礎知識，解決更為複雜問題一定有幫助。

鎮樓：