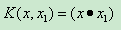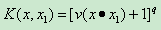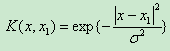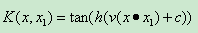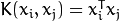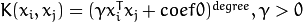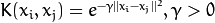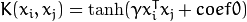opencv——SVM引數詳解
SVM是一種訓練機器學習的演算法,可以用於解決分類和迴歸問題,同時還使用了一種稱之為kernel trick(支援向量機的核函式)的技術進行資料的轉換,然後再根據這些轉換資訊,在可能的輸出之中找到一個最優的邊界(超平面)。簡單來說,就是做一些非常複雜的資料轉換工作,然後根據預定義的標籤或者輸出進而計算出如何分離使用者的資料。
支援向量機方法是建立在統計學習理論的VC 維理論和結構風險最小原理基礎上的,根據有限的樣本資訊在模型的複雜性(即對特定訓練樣本的學習精度,Accuracy)和學習能力(即無錯誤地識別任意樣本的能力)之間尋求最佳折衷,以期獲得最好的推廣能力
- 支援向量機較其他傳統機器學習演算法的優點:
-
1、小樣本,並不是說樣本的絕對數量少(實際上,對任何演算法來說,更多的樣本幾乎總是能帶來更好的效果),而是說與問題的複雜度比起來,SVM演算法要求的樣本數是相對比較少的。SVM解決問題的時候,和樣本的維數是無關的(甚至樣本是上萬維的都可以,這使得SVM很適合用來解決文字分類的問題,當然,有這樣的能力也因為引入了核函式)。
-
2、結構風險最小。(對問題真實模型的逼近與問題真實解之間的誤差,就叫做風險,更嚴格的說,誤差的累積叫做風險)。
-
3、非線性,是指SVM擅長應付樣本資料線性不可分的情況,主要通過鬆弛變數
(也有人叫懲罰變數)和核函式技術來實現,這一部分是SVM的精髓。(關於文字分類這個問題究竟是不是線性可分的,尚沒有定論,因此不能簡單的認為它是線性可分的而作簡化處理,在水落石出之前,只好先當它是線性不可分的反正線性可分也不過是線性不可分的一種特例而已,我們向來不怕方法過於通用)。
- SVM的強大離不開一個很重要的東西--核函式:
1、為何需要核函式?
很多情況下低維空間向量集是難於劃分的,解決辦法是將它們對映到高維空間。但這個辦法帶來的艱苦就是策畫錯雜度的增長,而核函式正好奇妙地解決了這個問題。也就是說,只要選用恰當的核函式,就可以獲得高維空間的分類函式(超平面)。在SVM理論中,採取不合的核函式將導致不合的SVM演算法。在斷定了核函式之後,因為斷定核函式的已知資料也存在必然的誤差,推敲到推廣性題目,是以引入了敗壞係數
其實核函式的本質作用可以簡練概括為:將低維空間的線性不可分類問題,藉助核函式轉化為高維空間的線性可分,進而可以在高維空間找到分類的最優邊界(超平面)。(下圖引自July‘s 支援向量機通俗導論(理解SVM的三層境界))。若要要分類下圖紅色和藍色樣本點:

2、核函式的分類
(1)線性核函式
(2)多項式核函式
(3)徑向基(RBF)核函式(高斯核函式)
(4)Sigmoid核函式(二層神經收集核函式)
3、Opencv中的核函式定義:
CvSVM::LINEAR : 線性核心,沒有任何向對映至高維空間,線性區分(或迴歸)在原始特點空間中被完成,這是最快的選擇。
.
CvSVM::POLY : 多項式核心:
.
CvSVM::RBF : 基於徑向的函式,對於大多半景象都是一個較好的選擇:
.
CvSVM::SIGMOID : Sigmoid函式核心:
.
- Opencv中SVM引數設定:
Opencv中SVM引數設定使用kernel方法定義如下:
enum KernelTypes {
/** Returned by SVM::getKernelType in case when custom kernel has been set */
CUSTOM=-1,
/** Linear kernel. No mapping is done, linear discrimination (or regression) is
done in the original feature space. It is the fastest option. \f$K(x_i, x_j) = x_i^T x_j\f$. */
LINEAR=0,
/** Polynomial kernel:
\f$K(x_i, x_j) = (\gamma x_i^T x_j + coef0)^{degree}, \gamma > 0\f$. */
POLY=1,
/** Radial basis function (RBF), a good choice in most cases.
\f$K(x_i, x_j) = e^{-\gamma ||x_i - x_j||^2}, \gamma > 0\f$. */
RBF=2,
/** Sigmoid kernel: \f$K(x_i, x_j) = \tanh(\gamma x_i^T x_j + coef0)\f$. */
SIGMOID=3,
/** Exponential Chi2 kernel, similar to the RBF kernel:
\f$K(x_i, x_j) = e^{-\gamma \chi^2(x_i,x_j)}, \chi^2(x_i,x_j) = (x_i-x_j)^2/(x_i+x_j), \gamma > 0\f$. */
CHI2=4,
/** Histogram intersection kernel. A fast kernel. \f$K(x_i, x_j) = min(x_i,x_j)\f$. */
INTER=5
};
kernel_type:SVM的核心型別(4種):
上面已經介紹過了就不再多說了。
svm_type:指定SVM的型別(5種):
1、CvSVM::C_SVC : C類支撐向量分類機。 n類分組 (n≥2),容許用異常值處罰因子C進行不完全分類。
2、CvSVM::NU_SVC :
類支撐向量分類機。n類似然不完全分類的分類器。引數為
庖代C(其值在區間【0,1】中,nu越大,決定計劃鴻溝越膩滑)。
3、CvSVM::ONE_CLASS : 單分類器,所有的練習資料提取自同一個類裡,然後SVM建樹了一個分界線以分別該類在特點空間中所佔區域和其它類在特點空間中所佔區域。
4、CvSVM::EPS_SVR :
類支撐向量迴歸機。練習集中的特點向量和擬合出來的超平面的間隔須要小於p。異常值處罰因子C被採取。
5、CvSVM::NU_SVR :
類支撐向量迴歸機。
庖代了 p。
degree:核心函式(POLY)的引數degree。
gamma:核心函式(POLY/ RBF/ SIGMOID)的引數 。
。
coef0:核心函式(POLY/ SIGMOID)的引數coef0。
Cvalue:SVM型別(C_SVC/ EPS_SVR/ NU_SVR)的引數C。
nu:SVM型別(NU_SVC/ ONE_CLASS/ NU_SVR)的引數  。
。
p:SVM型別(EPS_SVR)的引數 。
。
class_weights:C_SVC中的可選權重,賦給指定的類,乘以C今後變成  。所以這些權重影響不合類此外錯誤分類處罰項。權重越大,某一類此外誤分類資料的處罰項就越大。
。所以這些權重影響不合類此外錯誤分類處罰項。權重越大,某一類此外誤分類資料的處罰項就越大。
term_crit:SVM的迭代練習過程的中斷前提,解決專案組受束縛二次最優題目。您可以指定的公差和/或最大迭代次數。
- Opencv中SVM分類問題程式碼流程:
(1)獲得練習樣本及製作其類別標籤(trainingDataMat,labelsMat)
(2)設定練習引數(CvSVMParams)
(3)對SVM進行訓練(SVM::train)
(4)對新的輸入樣本進行猜測(SVM::predict),並輸出結果型別(對應標籤)
- SVM多類分類問題的幾種方法:
目前,構造SVM多類分類器的方法主要有兩類:一類是直接法,直接在目標函式上進行修改,將多個分類面的引數求解合併到一個最優化問題中,通過求解該最優化問題“一次性”實現多類分類。這種方法看似簡單,但其計算複雜度比較高,實現起來比較困難,只適合用於小型問題中;另一類是間接法,主要是通過組合多個二分類器來實現多分類器的構造,常見的方法有one-against-one和one-against-all兩種。
1、一對多法(one-versus-rest,簡稱OVRSVMs)。訓練時依次把某個類別的樣本歸為一類,其他剩餘的樣本歸為另一類,這樣k個類別的樣本就構造出了k個SVM。分類時將未知樣本分類為具有最大分類函式值的那類。
假如我有四類要劃分(也就是4個Label),他們是A、B、C、D。於是我在抽取訓練集的時候,分別抽取A所對應的向量作為正集,B,C,D所對應的向量作為負集;B所對應的向量作為正集,A,C,D所對應的向量作為負集;C所對應的向量作為正集,A,B,D所對應的向量作為負集;D所對應的向量作為正集,A,B,C所對應的向量作為負集,這四個訓練集分別進行訓練,然後的得到四個訓練結果檔案,在測試的時候,把對應的測試向量分別利用這四個訓練結果檔案進行測試,最後每個測試都有一個結果f1(x),f2(x),f3(x),f4(x).於是最終的結果便是這四個值中最大的一個。
PS:這種方法有種缺陷,因為訓練集是1:M,這種情況下存在偏差.因而不是很實用.
2、一對一法(one-versus-one,簡稱OVOSVMs或者pairwise)。其做法是在任意兩類樣本之間設計一個SVM,因此k個類別的樣本就需要設計k(k-1)/2個SVM。當對一個未知樣本進行分類時,最後得票最多的類別即為該未知樣本的類別。Libsvm中的多類分類就是根據這個方法實現的。
還是假設有四類A,B,C,D四類。在訓練的時候我選擇A,B;A,C; A,D; B,C;B,D;C,D所對應的向量作為訓練集,然後得到六個訓練結果,在測試的時候,把對應的向量分別對六個結果進行測試,然後採取投票形式,最後得到一組結果。
3、層次支援向量機(H-SVMs)。層次分類法首先將所有類別分成兩個子類,再將子類進一步劃分成兩個次級子類,如此迴圈,直到得到一個單獨的類別為止。
4、DAG-SVMS是由Platt提出的決策導向的迴圈圖DDAG匯出的,是針對“一對一”SVMS存在誤分、拒分現象提出的。
這裡僅僅是對幾種多分類方法的簡要說明,如果直接呼叫Opencv的predict方法,並不需要關心多分類演算法的具體實現,來看看下面的例子:
- Opencv中SVM多類分類問題程式設計例項:
-
void svmm_test() { //float trainingData1[16][2] = { { 0, 0 },{ 4, 1 },{ 4, 5 },{ -1, 6 },{ 3,11 },{ -2,10 },{ 4,30 },{ 0,25 },{ 10,13 },{ 15,12 },{ 25,40 },{ 11,35 },{ 8,1 },{ 9,6 },{ 15,5 },{ 20,-1 } }; //Mat trainingData = Mat(16, 2, CV_32FC1, trainingData1); // //Mat_<int> trainingLabels(1, 16); //trainingLabels << 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4; float trainingData1[10][2] = { { 0, 0 },{ 4, 0 },{ 0, 4 },{ 0, -4 },{ -4,0 },{ 8,0 },{ 0,8 },{ 0,-8 },{ -8,0 },{ 15,0 } }; Mat trainingData = Mat(10, 2, CV_32FC1, trainingData1); Mat_<int> trainingLabels(1, 10); trainingLabels << 1, 1, 1, 1, 1, 2, 2, 2, 2, 2; Ptr<ml::SVM> svm = ml::SVM::create(); /*一些設定的東西 svm->setType(ml::SVM::C_SVC);//設定svm型別 svm->setKernel(ml::SVM::POLY);//設定核函式 svm->setDegree(0.5); svm->setGamma(1); svm->setCoef0(1); svm->setNu(0.5); svm->setP(0); svm->setDegree(0.5); svm->setCoef0(1); svm->setGamma(1); */ svm->setType(ml::SVM::C_SVC); //svm->setKernel(ml::SVM::LINEAR); svm->setKernel(ml::SVM::RBF); svm->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER, 100, 1e-6)); svm->train(trainingData, ml::ROW_SAMPLE, trainingLabels); Mat_<float> testFeatures(1, 2); testFeatures << 1, 20; Mat res; for (int i = -15; i < 15; i++) { for (int j = -15; j < 15; j++) { testFeatures << i, j; svm->predict(testFeatures, res); int response = res.at<float>(0, 0); cout << response << " "; } cout << endl; } }