SVM引數詳解
svm引數說明----------------------
如果你要輸出類的概率,一定要有-b引數
svm-train training_set_file model_file
svm-predict test_file model_fileoutput_file
自動指令碼:python easy.py train_data test_data
自動選擇最優引數,自動進行歸一化。
對訓練集合和測試結合,使用同一個歸一化引數。
-c:引數
-g: 引數
-v:交叉驗證數
-s svm_type : set type of SVM (default 0)
0 -- C-SVC
1 -- nu-SVC
2 -- one-class SVM
3 -- epsilon-SVR
4 -- nu-SVR
-t kernel_type : set type of kernelfunction (default 2)
0 -- linear: u'*v
1 -- polynomial: (gamma*u'*v + coef0)^degree
2 -- radial basis function: exp(-gamma*|u-v|^2)
3 -- sigmoid: tanh(gamma*u'*v + coef0)
-d degree : set degree in kernel function(default 3)
-g gamma : set gamma in kernel function(default 1/num_features)
-r coef0 : set coef0 in kernel function(default 0)
-c cost : set the parameter C of C-SVC,epsilon-SVR, and nu-SVR (default 1)
-n nu : set the parameter nu of nu-SVC,one-class SVM, and nu-SVR (default 0.5)
-p epsilon : set the epsilon in lossfunction of epsilon-SVR (default 0.1)
-m cachesize : set cache memory size in MB(default 100)
-e epsilon : set tolerance of terminationcriterion (default 0.001)
-h shrinking: whether to use the shrinkingheuristics, 0 or 1 (default 1)
-b probability_estimates: whether to traina SVC or SVR model for probability estimates, 0 or 1 (default 0)(如果需要估計分到每個類的概率,則需要設定這個)
-wi weight: set the parameter C of class ito weight*C, for C-SVC (default 1)
Thek in the -g option means the number of attributes in the input data.
libsvm使用誤區----------------------
(1) 直接將訓練集合和測試集合簡單歸一化到[0,1]區間,可能導致實驗結果很差。
(2) 如果樣本的特徵數非常多,那麼就不必使用RBF核將樣本對映到高維空間。
a) 在特徵數非常多的情況下,使用線性核,結果已經非常好,並且只需要選擇引數C即可。
b) 雖然說RBF核的結果至少比線性核好,前提下搜尋整個的空間。
(3) 樣本數<<特徵數的情況:
a) 推薦使用線性核,可以達到與RBF同樣的效能。
(4) 樣本數和特徵數都非常多:推薦使用liblinear,更少的時間和記憶體,可比的準確率。
(5) 樣本數>>特徵數:如果想使用線性模型,可以使用liblinear,並且使用-s 2引數
libsvm在訓練model的時候,有如下引數要設定,當然有預設的引數,但是在具體應用方面效果會大大折扣。
Options:可用的選項即表示的涵義如下
-s svm型別:SVM設定型別(預設0)
0 -- C-SVC
1 --v-SVC
2 –一類SVM
3 -- e -SVR
4 -- v-SVR
-t 核函式型別:核函式設定型別(預設2)
0 –線性:u'v
1 –多項式:(r*u'v + coef0)^degree
2 – RBF函式:exp(-gamma|u-v|^2)
3 –sigmoid:tanh(r*u'v + coef0)
-d degree:核函式中的degree設定(針對多項式核函式)(預設3)
-g r(gama):核函式中的gamma函式設定(針對多項式/rbf/sigmoid核函式)(預設1/ k)
-r coef0:核函式中的coef0設定(針對多項式/sigmoid核函式)((預設0)
-c cost:設定C-SVC,e -SVR和v-SVR的引數(損失函式)(預設1)
-n nu:設定v-SVC,一類SVM和v- SVR的引數(預設0.5)
-p p:設定e -SVR 中損失函式p的值(預設0.1)
-m cachesize:設定cache記憶體大小,以MB為單位(預設40)
-e eps:設定允許的終止判據(預設0.001)
-h shrinking:是否使用啟發式,0或1(預設1)
-wi weight:設定第幾類的引數C為weight*C(C-SVC中的C)(預設1)
-v n: n-fold互動檢驗模式,n為fold的個數,必須大於等於2
其中-g選項中的k是指輸入資料中的屬性數。option -v 隨機地將資料剖分為n部
當構建完成model後,還要為上述引數選擇合適的值,方法主要有Gridsearch,其他的感覺不常用,Gridsearch說白了就是窮舉。
網格引數尋優函式(分類問題):SVMcgForClass
[bestCVaccuracy,bestc,bestg]=
SVMcgForClass(train_label,train,
cmin,cmax,gmin,gmax,v,cstep,gstep,accstep)
輸入:
train_label:訓練集的標籤,格式要求與svmtrain相同。
train:訓練集,格式要求與svmtrain相同。
cmin,cmax:懲罰引數c的變化範圍,即在[2^cmin,2^cmax]範圍內尋找最佳的引數c,預設值為cmin=-8,cmax=8,即預設懲罰引數c的範圍是[2^(-8),2^8]。
gmin,gmax:RBF核引數g的變化範圍,即在[2^gmin,2^gmax]範圍內尋找最佳的RBF核引數g,預設值為gmin=-8,gmax=8,即預設RBF核引數g的範圍是[2^(-8),2^8]。
v:進行Cross Validation過程中的引數,即對訓練集進行v-fold Cross Validation,預設為3,即預設進行3折CV過程。
cstep,gstep:進行引數尋優是c和g的步進大小,即c的取值為2^cmin,2^(cmin+cstep),…,2^cmax,,g的取值為2^gmin,2^(gmin+gstep),…,2^gmax,預設取值為cstep=1,gstep=1。
accstep:最後引數選擇結果圖中準確率離散化顯示的步進間隔大小([0,100]之間的一個數),預設為4.5。
輸出:
bestCVaccuracy:最終CV意義下的最佳分類準確率。
bestc:最佳的引數c。
bestg:最佳的引數g。
網格引數尋優函式(迴歸問題):SVMcgForRegress
[bestCVmse,bestc,bestg]=
SVMcgForRegress(train_label,train,
cmin,cmax,gmin,gmax,v,cstep,gstep,msestep)
其輸入輸出與SVMcgForClass類似,這裡不再贅述。
而當你訓練完了model,在用它做classification或regression之前,應該知道model中的內容,以及其含義。
用來訓練的是libsvm自帶的heart資料
model =
Parameters: [5x1 double]
nr_class: 2
totalSV: 259 % 支援向量的數目
rho: 0.0514 % b
Label: [2x1 double] % classification中標籤的個數
ProbA: []
ProbB: []
nSV: [2x1 double] % 每類支援向量的個數
sv_coef: [259x1 double] % 支援向量對應的Wi
SVs: [259x13 double] % 裝的是259個支援向量
model.Parameters引數意義從上到下依次為:
-s svm型別:SVM設定型別(預設0)
-t 核函式型別:核函式設定型別(預設2)
-d degree:核函式中的degree設定(針對多項式核函式)(預設3)
-g r(gama):核函式中的gamma函式設定(針對多項式/rbf/sigmoid核函式) (預設類別數目的倒數)
-r coef0:核函式中的coef0設定(針對多項式/sigmoid核函式)((預設0)
SVM 怎樣能得到好的結果
1. 對資料做歸一化(simple scaling)
2. 應用 RBF kernel
3. 用cross-validation和grid-search 得到最優的c和g
4. 用得到的最優c和g訓練訓練資料
5. 測試
關於svm的C以及核函式引數設定----------------------
參考自:對支援向量機幾種常用核函式和引數選擇的比較研究
C一般可以選擇為:10^t , t=- 4..4就是0.0001 到10000
選擇的越大,表示對錯誤例懲罰程度越大,可能會導致模型過擬合
在LIBSVM中-t用來指定核函式型別(預設值是2)。
0)線性核函式
(無其他引數)
1)多項式核函式
(重點是階數的選擇,即d,一般選擇1-11:1 3 5 7 9 11,也可以選擇2,4,6…)
2)RBF核函式
(徑向基RBF核心,exp{-|xi-xj|^2/均方差},其中均方差反映了資料波動的大小。
引數通常可選擇下面幾個數的倒數:0.1 0.2 0.4 0.6 0.8 1.6 3.2 6.4 12.8,預設的是類別數的倒數,即1/k,2分類的話就是0.5)
3)sigmoid核函式 又叫做S形核心
兩個引數g以及r:g一般可選1 2 3 4,r選0.2 0.4 0.60.8 1
4)自定義核函式
常用的四種核函式對應的公式如下:
與核函式相對應的libsvm引數:
1)對於線性核函式,沒有專門需要設定的引數
2)對於多項式核函式,有三個引數。-d用來設定多項式核函式的最高此項次數,也就是公式中的d,預設值是3。-g用來設定核函式中的gamma引數設定,也就是公式中的第一個r(gamma),預設值是1/k(k是類別數)。-r用來設定核函式中的coef0,也就是公式中的第二個r,預設值是0。
3)對於RBF核函式,有一個引數。-g用來設定核函式中的gamma引數設定,也就是公式中的第一個r(gamma),預設值是1/k(k是類別數)。
4)對於sigmoid核函式,有兩個引數。-g用來設定核函式中的gamma引數設定,也就是公式中的第一個r(gamma),預設值是1/k(k是類別數)。-r用來設定核函式中的coef0,也就是公式中的第二個r,預設值是0。
關於cost和gamma
SVM模型有兩個非常重要的引數C與gamma。其中 C是懲罰係數,即對誤差的寬容度。c越高,說明越不能容忍出現誤差,容易過擬合。C越小,容易欠擬合。C過大或過小,泛化能力變差
gamma是選擇RBF函式作為kernel後,該函式自帶的一個引數。隱含地決定了資料對映到新的特徵空間後的分佈,gamma越大,支援向量越少,gamma值越小,支援向量越多。支援向量的個數影響訓練與預測的速度。
此外大家注意RBF公式裡面的sigma和gamma的關係如下:
這裡面大家需要注意的就是gamma的物理意義,大家提到很多的RBF的幅寬,它會影響每個支援向量對應的高斯的作用範圍,從而影響泛化效能。我的理解:如果gamma設的太大,會很小,很小的高斯分佈長得又高又瘦, 會造成只會作用於支援向量樣本附近,對於未知樣本分類效果很差,存在訓練準確率可以很高,(如果讓無窮小,則理論上,高斯核的SVM可以擬合任何非線性資料,但容易過擬合)而測試準確率不高的可能,就是通常說的過訓練;而如果設的過小,則會造成平滑效應太大,無法在訓練集上得到特別高的準確率,也會影響測試集的準確率。
此外,可以明確的兩個結論是: 結論1:樣本數目少於特徵維度並不一定會導致過擬合,這可以參考餘凱老師的這句評論: “這不是原因啊,呵呵。用RBF kernel, 系統的dimension實際上不超過樣本數,與特徵維數沒有一個trivial的關係。”
結論2:RBF核應該可以得到與線性核相近的效果(按照理論,RBF核可以模擬線性核),可能好於線性核,也可能差於,但是,不應該相差太多。 當然,很多問題中,比如維度過高,或者樣本海量的情況下,大家更傾向於用線性核,因為效果相當,但是在速度和模型大小方面,線性核會有更好的表現。
老師木還有一句評論,可以加深初學者對SVM的理解: “須知rbf實際是記憶了若干樣例,在sv中各維權重重要性等同。線性核學出的權重是feature weighting作用或特徵選擇 。” 以上摘錄了:http://blog.sina.com.cn/s/blog_6ae183910101cxbv.html
Grid Search Grid Search是用在Libsvm中的引數搜尋方法。很容易理解:就是在C,gamma組成的二維引數矩陣中,依次實驗每一對引數的效果。
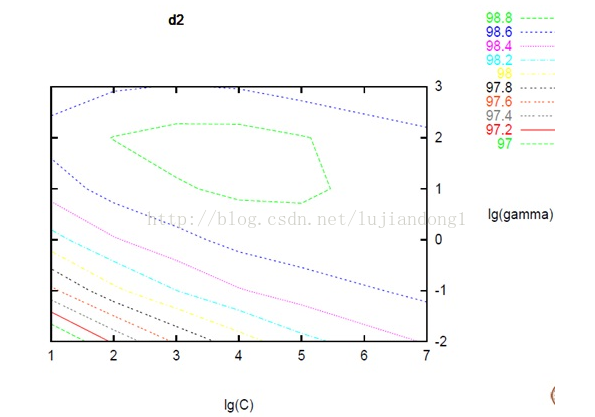
可以得到全域性最優 (C,gamma)相互獨立,便於並行化進行 # SVM Classifier using cross validation def svm_cross_validation(train_x, train_y): from sklearn.grid_search import GridSearchCV from sklearn.svm import SVC model = SVC(kernel='rbf', probability=True) param_grid = {'C': [1e-3, 1e-2, 1e-1, 1, 10, 100, 1000], 'gamma': [0.001, 0.0001]} grid_search = GridSearchCV(model, param_grid, n_jobs = 8, verbose=1) grid_search.fit(train_x, train_y) best_parameters = grid_search.best_estimator_.get_params() for para, val in list(best_parameters.items()): print(para, val) model = SVC(kernel='rbf', C=best_parameters['C'], gamma=best_parameters['gamma'], probability=True) model.fit(train_x, train_y) return model
SVM有如下主要幾個特點:
(1)非線性對映是SVM方法的理論基礎,SVM利用內積核函式代替向高維空間的非線性對映; (2)對特徵空間劃分的最優超平面是SVM的目標,最大化分類邊際的思想是SVM方法的核心; (3)支援向量是SVM的訓練結果,在SVM分類決策中起決定作用的是支援向量; (4)SVM 是一種有堅實理論基礎的新穎的小樣本學習方法。 它基本上不涉及概率測度及大數定律等,因此不同於現有的統計方法。 從本質上看,它避開了從歸納到演繹的傳統過程,實現了高效的從訓練樣本到預報樣本的“轉導推理”, 大大簡化了通常的分類和迴歸等問題;
(5)SVM 的最終決策函式只由少數的支援向量所確定,計算的複雜性取決於支援向量的數目, 而不是樣本空間的維數,這在某種意義上避免了“維數災難”。 (6)少數支援向量決定了最終結果,這不但可以幫助我們抓住關鍵樣本、“剔除”大量冗餘樣本, 而且註定了該方法不但演算法簡單,而且具有較好的“魯棒”性。 這種“魯棒”性主要體現在: ①增、刪非支援向量樣本對模型沒有影響;
②支援向量樣本集具有一定的魯棒性; ③有些成功的應用中,SVM 方法對核的選取不敏感 兩個不足: (1) SVM演算法對大規模訓練樣本難以實施 由於SVM是藉助二次規劃來求解支援向量, 而求解二次規劃將涉及m階矩陣的計算(m為樣本的個數),當m數目很大時該矩陣的儲存和計算 將耗費大量的機器記憶體和運算時間。 針對以上問題的主要改進有 J.Platt的SMO演算法、 T.Joachims的SVM、 C.J.C.Burges等的PCGC、 張學工的CSVM 以及O.L.Mangasarian等的SOR演算法 (2) 用SVM解決多分類問題存在困難 經典的支援向量機演算法只給出了二類分類的演算法, 而在資料探勘的實際應用中,一般要解決多類的分類問題。 可以通過多個二類支援向量機的組合來解決。 主要有 一對多組合模式、一對一組合模式和SVM決策樹; 再就是通過構造多個分類器的組合來解決。 主要原理是克服SVM固有的缺點,結合其他演算法的優勢,解決多類問題的分類精度。 如: 與粗集理論結合,形成一種優勢互補的多類問題的組合分類器。
--------------------- 原文:https://blog.csdn.net/bryan__/article/details/51506801
