文章基於此篇微信推送https://mp.weixin.qq.com/s/3h9iqU4rdH3EIy5m6AzXsg

簡介

動態規劃是一種由問題的最小子狀態（邊界）不斷推出更大的狀態，最後解決整個問題的解題思想。

基礎概念

1. 最優子結構：狀態可被分解為的子狀態
2. 邊界：無需在繼續簡化的最小子狀態
3. 狀態轉移公式：狀態與其子狀態間關係的描述公式
4. 記憶話搜尋：將每個狀態對應的值記錄下來，遇到相同的狀態時就直接返回值，而不需要重複計算。

例題講解

有一個國家發現了5座金礦，每座金礦的黃金儲量不同，需要參與挖掘的工人數也不同。參與挖礦工人的總數是10人。每座金礦要麼全挖，要麼不挖，不能派出一半人挖取一半金礦。要求用程式求解出，要想得到儘可能多的黃金，應該選擇挖取哪幾座金礦？

解答：

1.尋找最優子結構

4金礦10工人時的最優選擇和4金礦（10-第五個金礦所需工人）時的最優選擇。

2.尋找狀態轉移方程

a. 設金礦數量為n，工人數量為w，金礦的黃金量為G[ ],金礦的用工量為P[ ]。例如5坐金礦和4坐金礦之間的最優選擇存在關係：F(5,10)=max(F(4,10),F(4,10-P[4]+G[4]))

b. 確定問題邊界

當工人數量w大於等於最後一個金礦用工量P[0]時，F(n,w)=G[0]

當工人數量w小於最後一個金礦用工量P[0]時，F[n,w]=0

c. 總結得到狀態注意方程（組）

F(n,w) = 0    (n<=1, w<p[0]);

F(n,w) = g[0]     (n==1, w>=p[0]);

F(n,w) = F(n-1,w)    (n>1, w<p[n-1]) 

F(n,w) = max(F(n-1,w),  F(n-1,w-p[n-1])+g[n-1])    (n>1, w>=p[n-1])

3.實現

a. 分析

說明：

   第一列代表給定的1-5座金礦的情況

   第一行代表剩餘工人數，即w

   空格表示F(n,w)

第一座金礦：400金，需5人

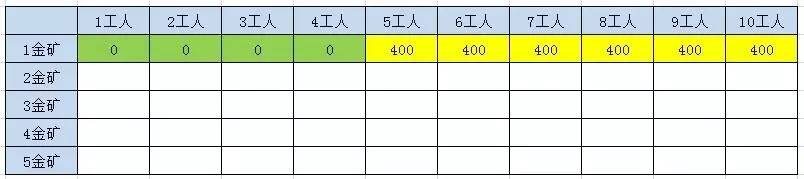
第二座金礦500金，需5人

第三座金礦200金，需3人  

第四座金礦300金，需4工人 

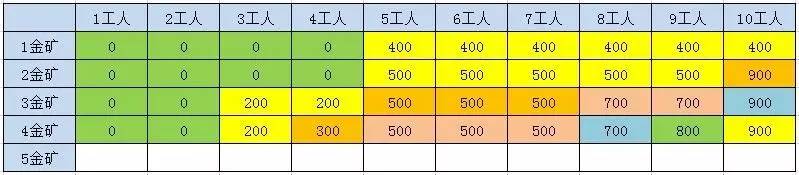
第五座金礦350金，需3工人

歸納：

每個狀態都有前一行的狀態推導而來。例如3金礦8工人的結果來自於Max（500，500+200），即2金礦5工人和2金礦8工人。所以只要知道最初的狀態，就可以推匯出最終的結果。

最終程式碼：