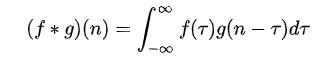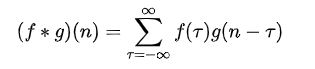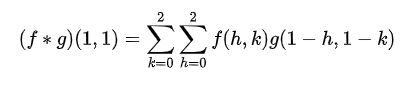本文主要為下面兩篇篇文章加自己的理解感悟總結而來

1.知乎高贊回答如何通俗易懂地解釋卷積？

2.知乎高贊回答卷積為什麼叫「卷」積？

預備知識

  1.向量運算

• 點乘（a * b）

      向量的點乘,也叫向量的內積、數量積，點積。對兩個向量執行點乘運算，就是對這兩個向量對應位一一相乘之後求和的操    作，點乘的結果是一個標量。

• 叉乘（a ∧ b）

      兩個向量的叉乘，又叫向量積、外積、叉積。叉乘的運算結果是一個向量。並且兩個向量的叉積與這兩個向量組成的座標平面垂直（即法向量）。

      注：本文用不到叉積，這裡寫出來只是為了幫助辨析概念

  2.張量

張量是一種表示物理量的方式。張量的階數可以簡單的理解為其基向量的維度。例如標量沒有基向量，所以它是0階張量，向量的基向量為一維，所以它為1階張量。以此類推。

具體可以參考此篇文章：怎麼通俗地理解張量?

卷積的定義及其理解

我們稱 (f*g)(n) 為 f,g 的卷積

其連續的定義為：

其離散的定義為：

這兩個式子有一個共同的特徵：

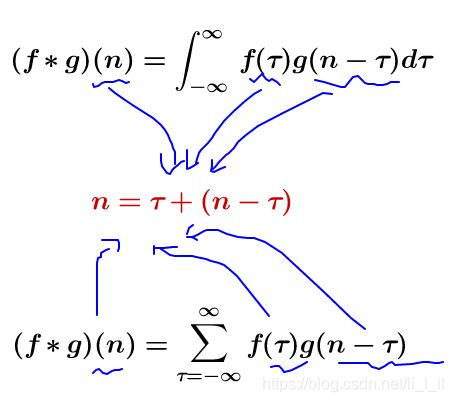
我們令 x=t ,y=n-t  ，那麼 x+y=n 就是下面這些直線：

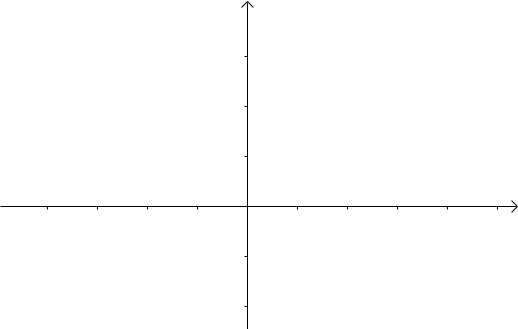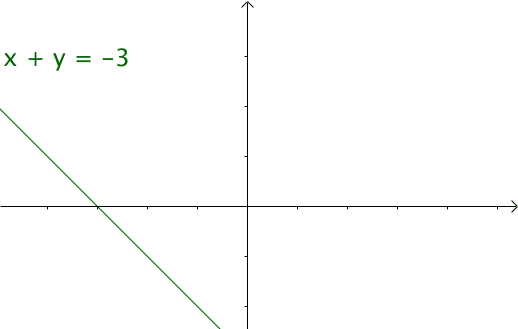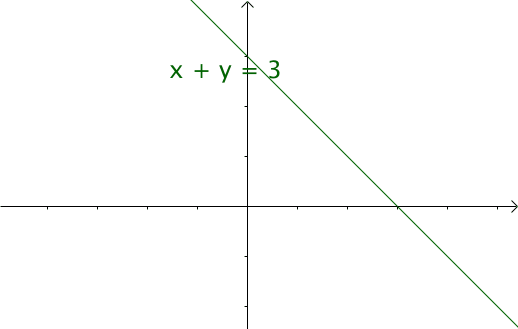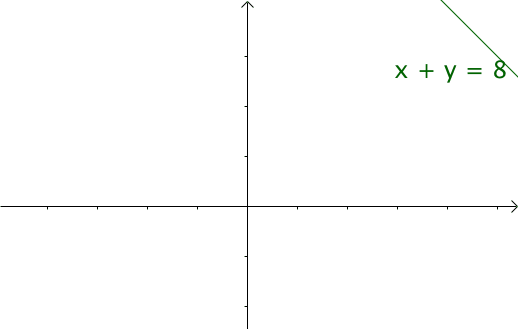
將以上座標系看作一個平面。將該平面升高一個維度，得到下圖

上面儲存著f和g在區間[a,b]上的張量積，即U(x,y)=f(x)g(y)。則直線x+y=n上對應點的張量積的積分就是(f*g)(n)對應的卷積值。本例對應的計算公式如下

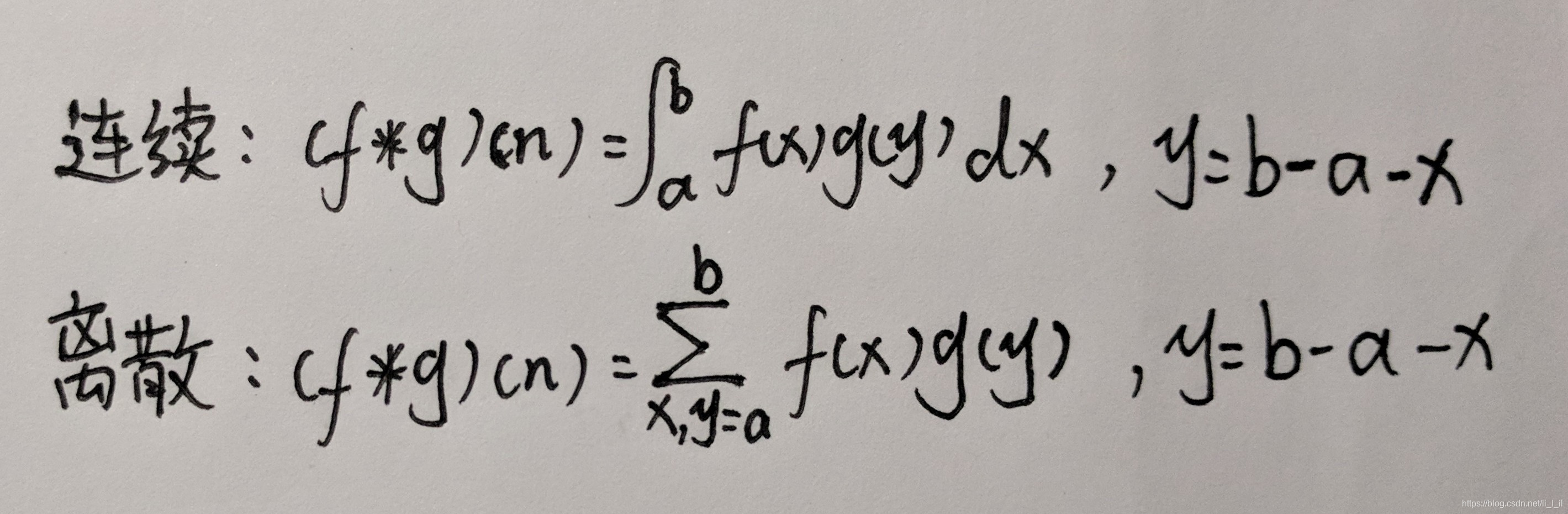
為什麼叫“卷積”

接上例，把平面一角捲起來

將整個平面捲起來後，便降維到了一條直線，即變成了一個一維的函式，而且直線上每點的函式值等於捲起來後重合的點函式值之和。

再將平面攤開

可以看出，被畫了線的地方，正好就是x+y為定值的一條直線，所以捲起來後那點的函式值正好為這條直線上函式值的積分，也即等於卷積值。這便是“卷積”的由來。

卷積值的計算

根據定義，對上圖的兩個矩陣進行卷積，計算過程如下動圖所示

寫成卷積公式就是：

進行卷積時為什麼把運算元旋轉180°

上面的式子用程式碼實現起來是有點複雜的，如果只是矩陣對應位置的數值相乘就會方便很多！那有沒有什麼辦法做到這一點呢？答案是有，當把一個矩陣旋轉180°後，兩個矩陣對應位置乘積的和就等於根據定義計算得到的乘積和。所以為了方便計算，人們在進行卷積時往往把運算元進行旋轉，然後直接計算對應位置的乘積和。

卷積過程概覽

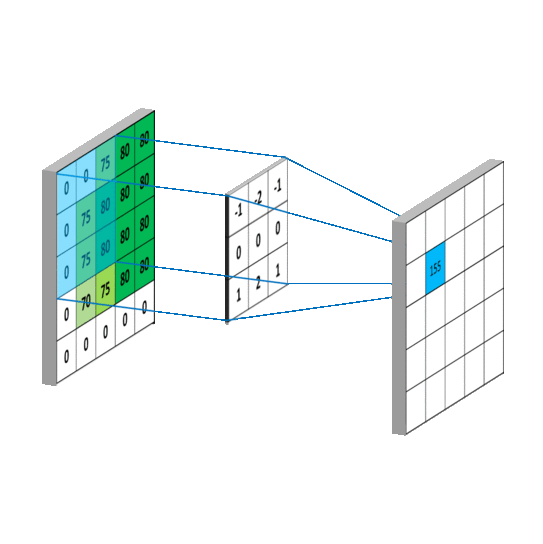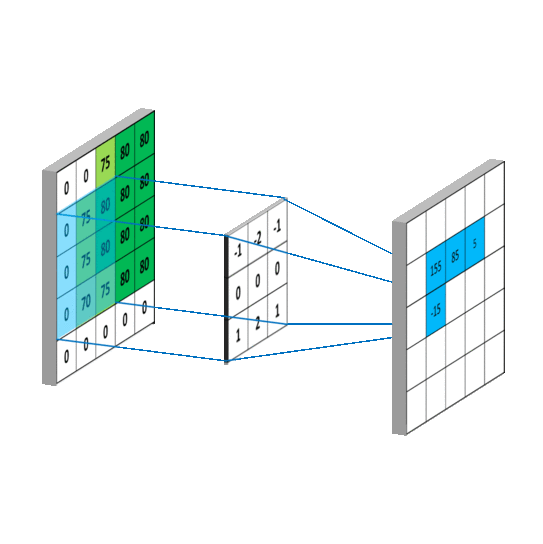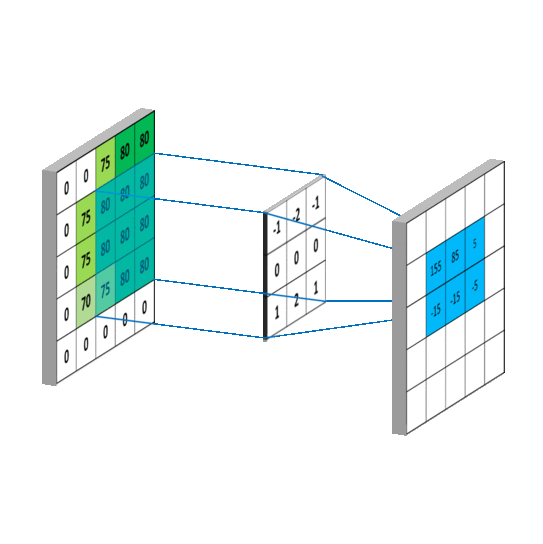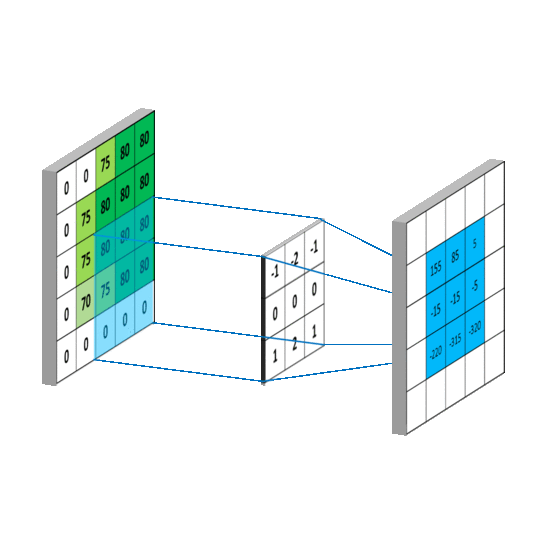
注意：上面的卷積核是經過180°旋轉後的，所以才能以對應位置乘積的和做為卷積值