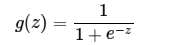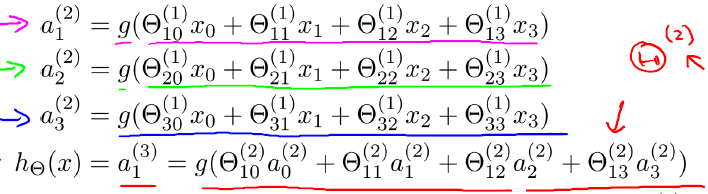CNN筆記 通俗理解卷積神經網路
通俗理解卷積神經網路（cs231n與5月dl班課程筆記）
1 前言
2012年我在北京組織過8期machine learning讀書會，那時“機器學習”非常火，很多人都對其抱有巨大的熱情。當我2013年再次來到北京時，有一個詞似乎比“機器學習”更火，那就是“深度學習”。
本部落格內寫過一些機器學習相關的文章，但上一篇技術文章“LDA主題模型”還是寫於2014年11月份，畢竟自2015年開始創業做線上教育後，太多的雜事、瑣碎事，讓我一直想再寫點技術性文章但每每恨時間抽不開。然由於公司在不斷開機器學習、深度學習等相關的線上課程，耳濡目染中，總會順帶著學習學習。
我雖不參與講任何課程（我所在公司“
在dl中，有一個很重要的概念，就是卷積神經網路CNN，基本是入門dl必須搞懂的東西。本文基本根據斯坦福的機器學習公開課、cs231n、與七月線上寒小陽講的5月dl班第4次課CNN與常用框架視訊所寫，是一篇課程筆記。
一開始本文只是想重點講下CNN中的卷積操作具體是怎麼計算怎麼操作的，但後面不斷補充，包括增加不少自己的理解，故寫成了關於卷積神經網路的通俗導論性的文章。有何問題，歡迎不吝指正。
2 人工神經網路
2.1 神經元
神經網路由大量的神經元相互連線而成。每個神經元接受線性組合的輸入後，最開始只是簡單的線性加權，後來給每個神經元加上了非線性的啟用函式，從而進行非線性變換後輸出。每兩個神經元之間的連線代表加權值，稱之為權重（weight）。不同的權重和啟用函式，則會導致神經網路不同的輸出。
舉個手寫識別的例子，給定一個未知數字，讓神經網路識別是什麼數字。此時的神經網路的輸入由一組被輸入影象的畫素所啟用的輸入神經元所定義。在通過非線性啟用函式進行非線性變換後，神經元被啟用然後被傳遞到其他神經元。重複這一過程，直到最後一個輸出神經元被啟用。從而識別當前數字是什麼字。
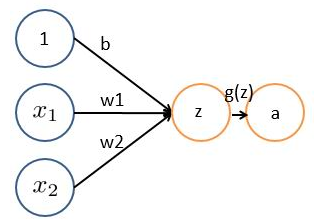
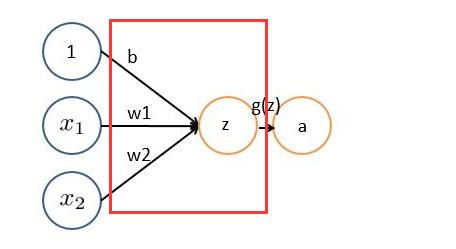
神經網路的每個神經元如下
基本wx + b的形式，其中
、
表示輸入向量
、
為權重，幾個輸入則意味著有幾個權重，即每個輸入都被賦予一個權重
- b為偏置bias
- g(z) 為啟用函式
- a 為輸出
如果只是上面這樣一說，估計以前沒接觸過的十有八九又必定迷糊了。事實上，上述簡單模型可以追溯到20世紀50/60年代的感知器，可以把感知器理解為一個根據不同因素、以及各個因素的重要性程度而做決策的模型。
舉個例子，這週末北京有一草莓音樂節，那去不去呢？決定你是否去有二個因素，這二個因素可以對應二個輸入，分別用x1、x2表示。此外，這二個因素對做決策的影響程度不一樣，各自的影響程度用權重w1、w2表示。一般來說，音樂節的演唱嘉賓會非常影響你去不去，唱得好的前提下 即便沒人陪同都可忍受，但如果唱得不好還不如你上臺唱呢。所以，我們可以如下表示：
這樣，咱們的決策模型便建立起來了：g(z) = g(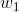
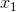
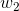
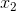
一開始為了簡單，人們把啟用函式定義成一個線性函式，即對於結果做一個線性變化，比如一個簡單的線性啟用函式是g(z) = z，輸出都是輸入的線性變換。後來實際應用中發現，線性啟用函式太過侷限，於是人們引入了非線性啟用函式。
2.2 啟用函式
常用的非線性啟用函式有sigmoid、tanh、relu等等，前兩者sigmoid/tanh比較常見於全連線層，後者relu常見於卷積層。這裡先簡要介紹下最基礎的sigmoid函式（btw，在本部落格中SVM那篇文章開頭有提過）。
sigmoid的函式表示式如下
其中z是一個線性組合，比如z可以等於：b +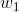
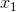
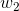
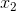
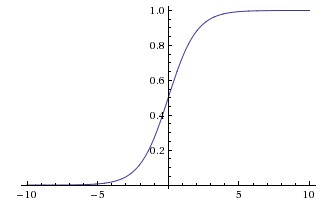
因此，sigmoid函式g(z)的圖形表示如下（ 橫軸表示定義域z，縱軸表示值域g(z) ）：
也就是說，sigmoid函式的功能是相當於把一個實數壓縮至0到1之間。當z是非常大的正數時，g(z)會趨近於1，而z是非常小的負數時，則g(z)會趨近於0。
壓縮至0到1有何用處呢？用處是這樣一來便可以把啟用函式看作一種“分類的概率”，比如啟用函式的輸出為0.9的話便可以解釋為90%的概率為正樣本。
舉個例子，如下圖（圖引自Stanford機器學習公開課）
z = b +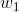
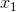
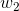
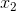
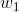
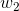
- 如果
- 如果
- 如果
換言之，只有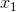
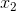
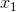
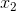
2.3 神經網路
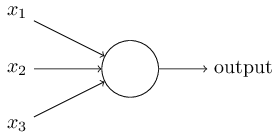
將下圖的這種單個神經元
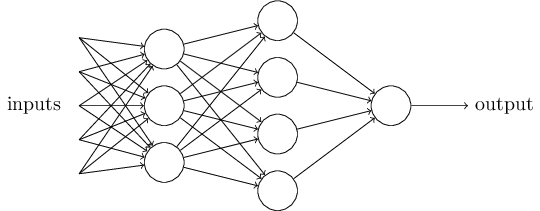
組織在一起，便形成了神經網路。下圖便是一個三層神經網路結構
上圖中最左邊的原始輸入資訊稱之為輸入層，最右邊的神經元稱之為輸出層（上圖中輸出層只有一個神經元），中間的叫隱藏層。
啥叫輸入層、輸出層、隱藏層呢？
- 輸入層（Input layer），眾多神經元（Neuron）接受大量非線形輸入訊息。輸入的訊息稱為輸入向量。
- 輸出層（Output layer），訊息在神經元連結中傳輸、分析、權衡，形成輸出結果。輸出的訊息稱為輸出向量。
- 隱藏層（Hidden layer），簡稱“隱層”，是輸入層和輸出層之間眾多神經元和連結組成的各個層面。如果有多個隱藏層，則意味著多個啟用函式。
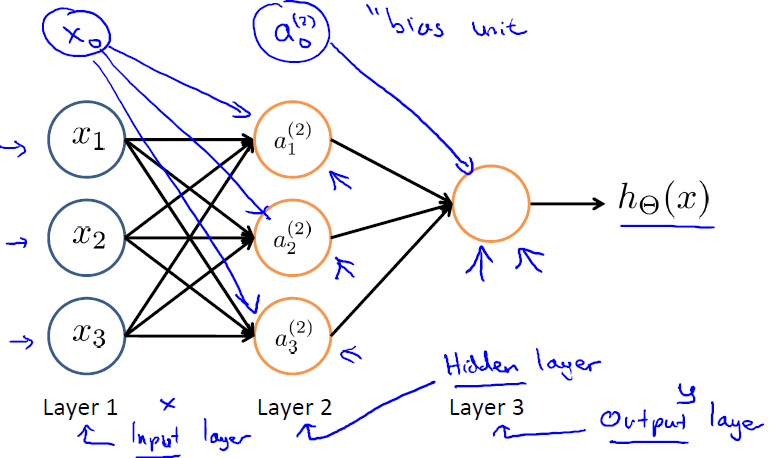
同時，每一層都可能由單個或多個神經元組成，每一層的輸出將會作為下一層的輸入資料。比如下圖中間隱藏層來說，隱藏層的3個神經元a1、a2、a3皆各自接受來自多個不同權重的輸入（因為有x1、x2、x3這三個輸入，所以a1 a2 a3都會接受x1 x2 x3各自分別賦予的權重，即幾個輸入則幾個權重），接著，a1、a2、a3又在自身各自不同權重的影響下 成為的輸出層的輸入，最終由輸出層輸出最終結果。
上圖（圖引自Stanford機器學習公開課）中
表示第j層第i個單元的啟用函式/神經元
表示從第j層對映到第j+1層的控制函式的權重矩陣
此外，輸入層和隱藏層都存在一個偏置（bias unit)，所以上圖中也增加了偏置項：x0、a0。針對上圖，有如下公式
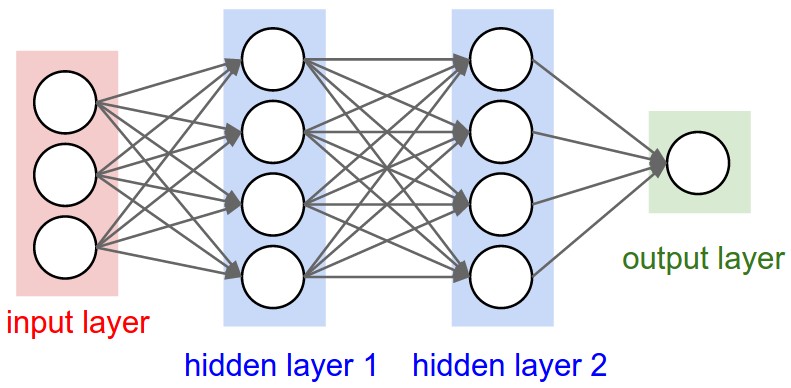
此外，上文中講的都是一層隱藏層，但實際中也有多層隱藏層的，即輸入層和輸出層中間夾著數層隱藏層，層和層之間是全連線的結構，同一層的神經元之間沒有連線。
3 卷積神經網路之層級結構
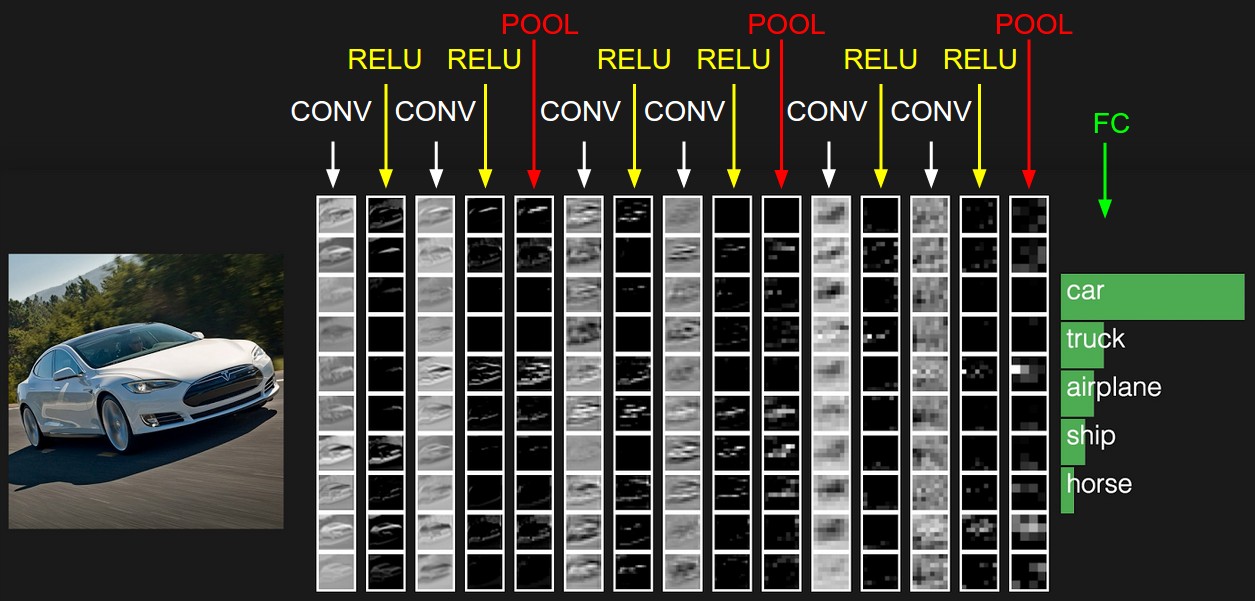
cs231n課程裡給出了卷積神經網路各個層級結構，如下圖
上圖中CNN要做的事情是：給定一張圖片，是車還是馬未知，是什麼車也未知，現在需要模型判斷這張圖片裡具體是一個什麼東西，總之輸出一個結果：如果是車 那是什麼車
所以
- 最左邊是資料輸入層，對資料做一些處理，比如去均值（把輸入資料各個維度都中心化為0，避免資料過多偏差，影響訓練效果）、歸一化（把所有的資料都歸一到同樣的範圍）、PCA/白化等等。CNN只對訓練集做“去均值”這一步。
中間是
- CONV：卷積計算層，線性乘積 求和。
- RELU：激勵層，上文2.2節中有提到：ReLU是啟用函式的一種。
- POOL：池化層，簡言之，即取區域平均或最大。
最右邊是
- FC：全連線層
這幾個部分中，卷積計算層是CNN的核心，下文將重點闡述。
4 CNN之卷積計算層
4.1 CNN怎麼進行識別
當我們給定一個"X"的圖案，計算機怎麼識別這個圖案就是“X”呢？一個可能的辦法就是計算機儲存一張標準的“X”圖案，然後把需要識別的未知圖案跟標準"X"圖案進行比對，如果二者一致，則判定未知圖案即是一個"X"圖案。
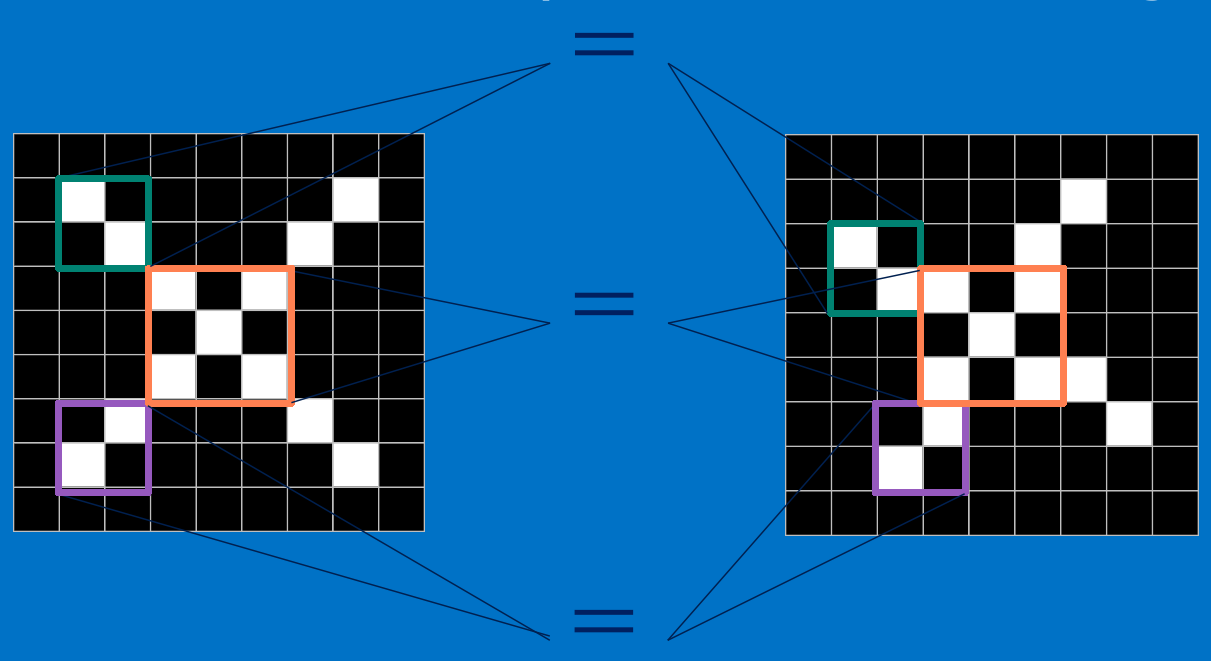
而且即便未知圖案可能有一些平移或稍稍變形，依然能辨別出它是一個X圖案。如此，CNN是把未知圖案和標準X圖案一個區域性一個區域性的對比，如下圖所示 [圖來自參考文案25]
而未知圖案的區域性和標準X圖案的區域性一個一個比對時的計算過程，便是卷積操作。卷積計算結果為1表示匹配，否則不匹配。
接下來，我們來了解下什麼是卷積操作。
4.2 什麼是卷積
對影象（不同的資料視窗資料）和濾波矩陣（一組固定的權重：因為每個神經元的多個權重固定，所以又可以看做一個恆定的濾波器filter）做內積（逐個元素相乘再求和）的操作就是所謂的『卷積』操作，也是卷積神經網路的名字來源。
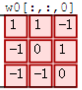
非嚴格意義上來講，下圖中紅框框起來的部分便可以理解為一個濾波器，即帶著一組固定權重的神經元。多個濾波器疊加便成了卷積層。
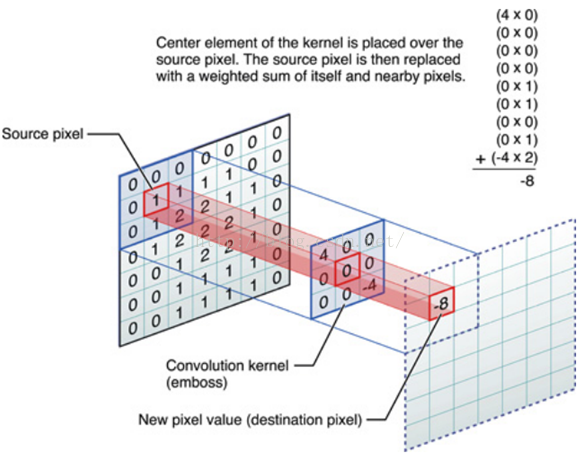
OK，舉個具體的例子。比如下圖中，圖中左邊部分是原始輸入資料，圖中中間部分是濾波器filter，圖中右邊是輸出的新的二維資料。
分解下上圖
對應位置上是數字先相乘後相加
=
中間濾波器filter與資料視窗做內積，其具體計算過程則是：4*0 + 0*0 + 0*0 + 0*0 + 0*1 + 0*1 + 0*0 + 0*1 + -4*2 = -8
4.3 影象上的卷積
在下圖對應的計算過程中，輸入是一定區域大小(width*height)的資料，和濾波器filter（帶著一組固定權重的神經元）做內積後等到新的二維資料。
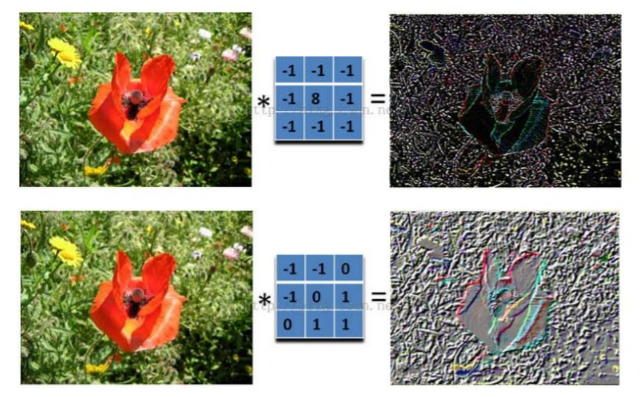
具體來說，左邊是影象輸入，中間部分就是濾波器filter（帶著一組固定權重的神經元），不同的濾波器filter會得到不同的輸出資料，比如顏色深淺、輪廓。相當於如果想提取影象的不同特徵，則用不同的濾波器filter，提取想要的關於影象的特定資訊：顏色深淺或輪廓。
如下圖所示
4.4 GIF動態卷積圖
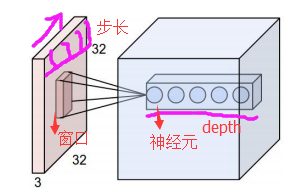
在CNN中，濾波器filter（帶著一組固定權重的神經元）對區域性輸入資料進行卷積計算。每計算完一個數據視窗內的區域性資料後，資料視窗不斷平移滑動，直到計算完所有資料。這個過程中，有這麼幾個引數： a. 深度depth：神經元個數，決定輸出的depth厚度。同時代表濾波器個數。 b. 步長stride：決定滑動多少步可以到邊緣。
c. 填充值zero-padding：在外圍邊緣補充若干圈0，方便從初始位置以步長為單位可以剛好滑倒末尾位置，通俗地講就是為了總長能被步長整除。
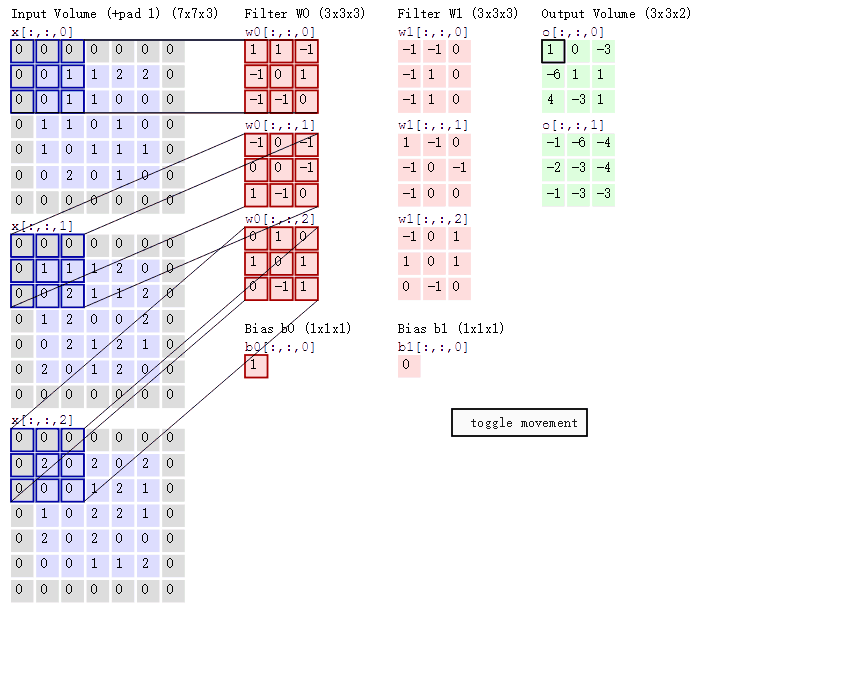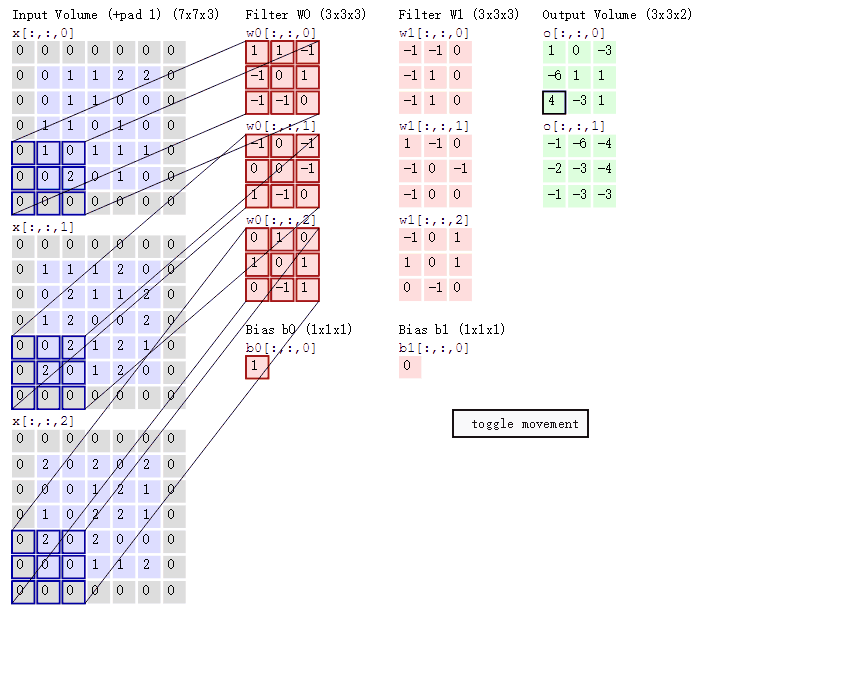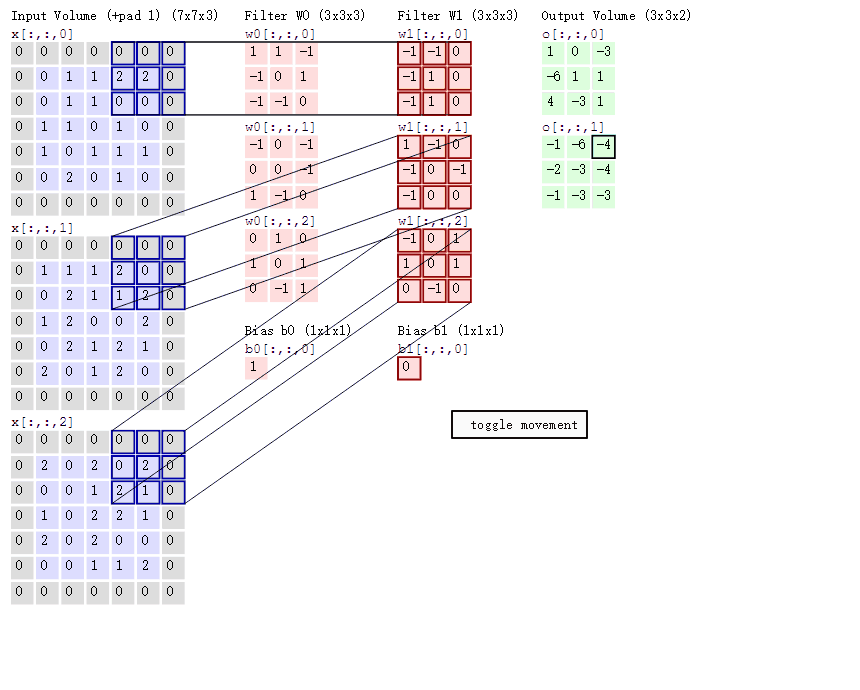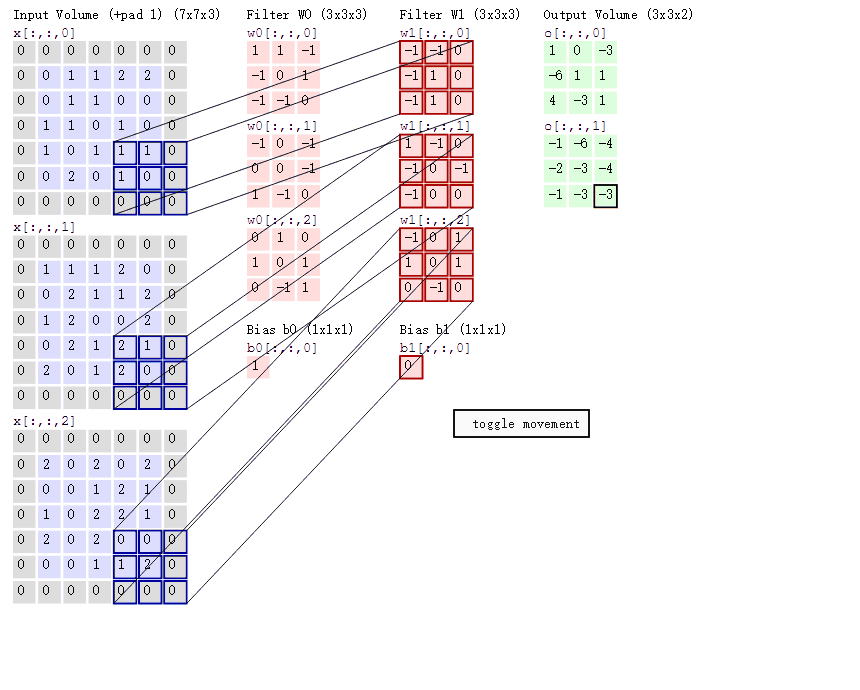
cs231n課程中有一張卷積動圖，貌似是用d3js 和一個util 畫的，我根據cs231n的卷積動圖依次截取了18張圖，然後用一gif 製圖工具製作了一gif 動態卷積圖。如下gif 圖所示
可以看到：
- 兩個神經元，即depth=2，意味著有兩個濾波器。
- 資料視窗每次移動兩個步長取3*3的區域性資料，即stride=2。
- zero-padding=1。
然後分別以兩個濾波器filter為軸滑動陣列進行卷積計算，得到兩組不同的結果。
如果初看上圖，可能不一定能立馬理解啥意思，但結合上文的內容後，理解這個動圖已經不是很困難的事情：
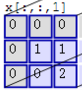
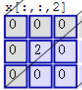
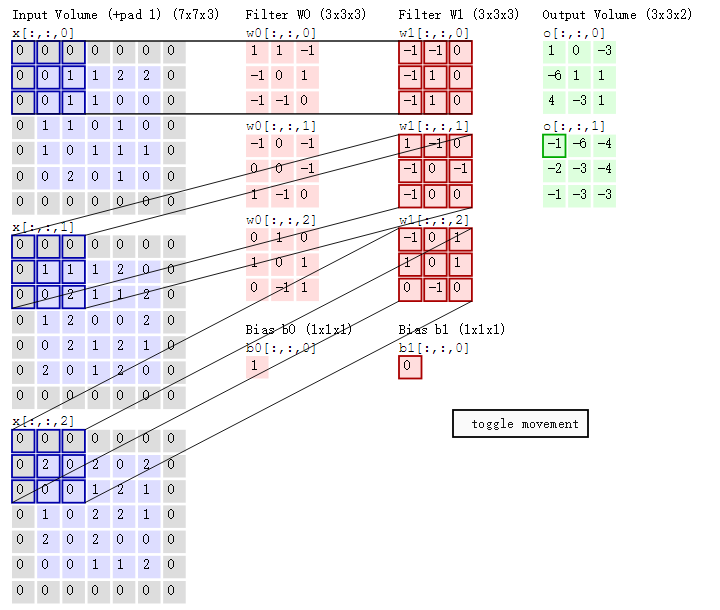
- 左邊是輸入（7*7*3中，7*7代表影象的畫素/長寬，3代表R、G、B 三個顏色通道）
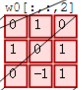
- 中間部分是兩個不同的濾波器Filter w0、Filter w1
- 最右邊則是兩個不同的輸出
隨著左邊資料視窗的平移滑動，濾波器Filter w0 / Filter w1對不同的區域性資料進行卷積計算。
值得一提的是：
- 左邊資料在變化，每次濾波器都是針對某一區域性的資料視窗進行卷積，這就是所謂的CNN中的區域性感知機制。
- 打個比方，濾波器就像一雙眼睛，人類視角有限，一眼望去，只能看到這世界的區域性。如果一眼就看到全世界，你會累死，而且一下子接受全世界所有資訊，你大腦接收不過來。當然，即便是看區域性，針對區域性裡的資訊人類雙眼也是有偏重、偏好的。比如看美女，對臉、胸、腿是重點關注，所以這3個輸入的權重相對較大。
與此同時，資料視窗滑動，導致輸入在變化，但中間濾波器Filter w0的權重（即每個神經元連線資料視窗的權重）是固定不變的，這個權重不變即所謂的CNN中的引數（權重）共享機制。
- 再打個比方，某人環遊全世界，所看到的資訊在變，但採集資訊的雙眼不變。btw，不同人的雙眼 看同一個區域性資訊 所感受到的不同，即一千個讀者有一千個哈姆雷特，所以不同的濾波器 就像不同的雙眼，不同的人有著不同的反饋結果。
我第一次看到上面這個動態圖的時候，只覺得很炫，另外就是據說計算過程是“相乘後相加”，但到底具體是個怎麼相乘後相加的計算過程 則無法一眼看出，網上也沒有一目瞭然的計算過程。本文來細究下。
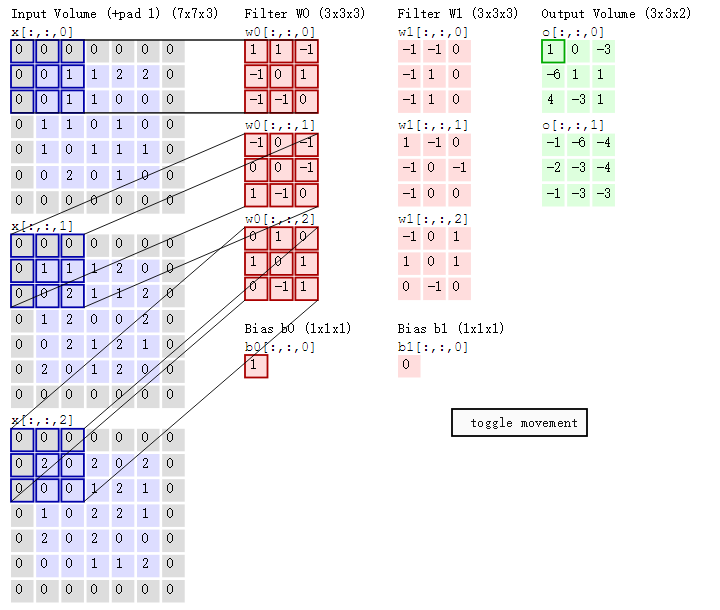
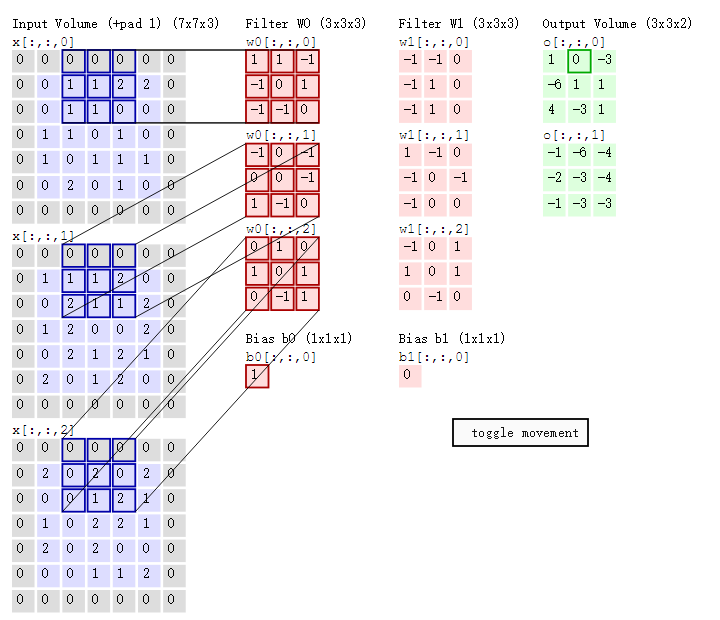
首先，我們來分解下上述動圖，如下圖
接著，我們細究下上圖的具體計算過程。即上圖中的輸出結果1具體是怎麼計算得到的呢？其實，類似wx + b，w對應濾波器Filter w0，x對應不同的資料視窗，b對應Bias b0，相當於濾波器Filter w0與一個個資料視窗相乘再求和後，最後加上Bias b0得到輸出結果1，如下過程所示：
1* 0 + 1*0 + -1*0
+
-1*0 + 0*0 + 1*1
+
-1*0 + -1*0 + 0*1
+
-1*0 + 0*0 + -1*0
+
0*0 + 0*1 + -1*1
+
1*0 + -1*0 + 0*2
+
0*0 + 1*0 + 0*0
+
1*0 + 0*2 + 1*0
+
0*0 + -1*0 +1*0
+
1
=
1
然後濾波器Filter w0固定不變，資料視窗向右移動2步，繼續做內積計算，得到0的輸出結果
最後，換做另外一個不同的濾波器Filter w1、不同的偏置Bias b1，再跟圖中最左邊的資料視窗做卷積，可得到另外一個不同的輸出。
5 CNN之激勵層與池化層
5.1 ReLU激勵層
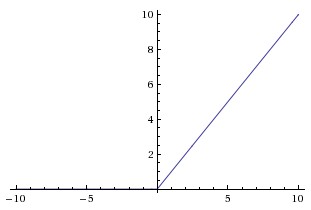
2.2節介紹了啟用函式sigmoid，但實際梯度下降中，sigmoid容易飽和、造成終止梯度傳遞，且沒有0中心化。咋辦呢，可以嘗試另外一個啟用函式：ReLU，其圖形表示如下
ReLU的優點是收斂快，求梯度簡單。
5.2 池化pool層
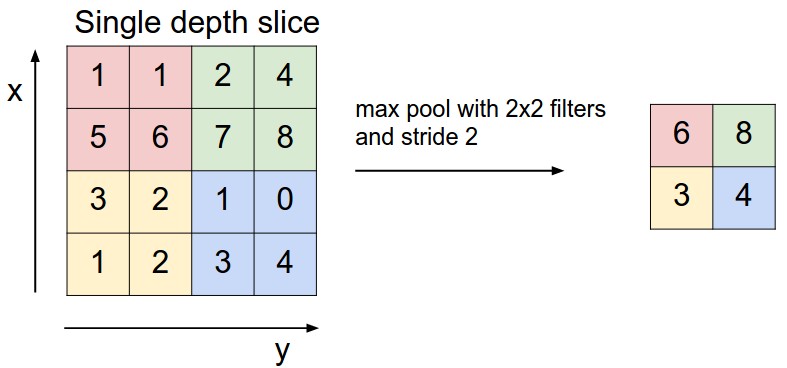
前頭說了，池化，簡言之，即取區域平均或最大，如下圖所示（圖引自cs231n）
上圖所展示的是取區域最大，即上圖左邊部分中 左上角2x2的矩陣中6最大，右上角2x2的矩陣中8最大，左下角2x2的矩陣中3最大，右下角2x2的矩陣中4最大，所以得到上圖右邊部分的結果：6 8 3 4。很簡單不是？
6 後記
本文基本上邊看5月dl班寒講的CNN視訊邊做筆記，之前斷斷續續看過不少CNN相關的資料（包括cs231n），但看過視訊之後，才系統瞭解CNN到底是個什麼東西，作為聽眾 寒講的真心贊、清晰。然後在寫CNN相關的東西時，發現一些前置知識（比如神經元、多層神經網路等也需要介紹下），包括CNN的其它層次機構（比如激勵層），所以本文字只想簡要介紹下卷積操作的，但考慮到知識之間的前後關聯，所以越寫越長，便成本文了。
此外，在寫作本文的過程中，請教了我們講師團隊裡的寒、馮兩位，感謝他兩。同時，感謝愛可可老師的微博轉發，感謝七月線上所有同事。
以下是修改日誌：
- 2016年7月5日，修正了一些筆誤、錯誤，以讓全文更通俗、更精準。有任何問題或槽點，歡迎隨時指出。
- 2016年7月7日，第二輪修改完畢。且根據cs231n的卷積動圖依次截取了18張圖，然後用製圖工具製作了一gif 動態卷積圖，放在文中4.3節。
- 2016年7月16日，完成第三輪修改。本輪修改主要體現在sigmoid函式的說明上，通過舉例和統一相關符號讓其含義更一目瞭然、更清晰。
- 2016年8月15日，完成第四輪修改，增補相關細節。比如補充4.3節GIF動態卷積圖中輸入部分的解釋，即7*7*3的含義（其中7*7代表影象的畫素/長寬，3代表R、G、B 三個顏色通道）。不斷更易懂。
- 2016年8月22日，完成第五輪修改。本輪修改主要加強濾波器的解釋，及引入CNN中濾波器的通俗比喻。
July、最後修改於二零一六年八月二十二日中午於七月線上辦公室。