深層神經網路（Deep L-layer neural network）

目前為止我們已經學習了只有一個單獨隱藏層的神經網路的正向傳播和反向傳播，還有邏輯迴歸，並且你還學到了向量化，這在隨機初始化權重時是很重要。

目前所要做的是把這些理念集合起來，就可以執行你自己的深度神經網路。

複習下前面21個筆記的內容：

邏輯迴歸，結構如下圖左邊。一個隱藏層的神經網路，結構下圖右邊：

注意，神經網路的層數是這麼定義的：從左到右，由0開始定義，比如上邊右圖，x_1、x_2、x_3,這層是第0層，這層左邊的隱藏層是第1層，由此類推。

如下圖左邊是兩個隱藏層的神經網路，右邊是5個隱藏層的神經網路。(也就是說剛輸入層不算一層神經網路，這個概念也記住哦，再次說明)

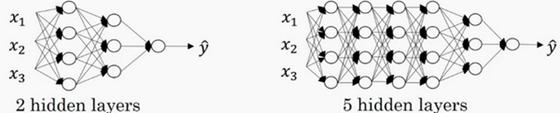
嚴格上來說邏輯迴歸也是一個一層的神經網路，而上邊右圖一個深得多的模型，淺與深僅僅是指一種程度。

記住以下要點：

有一個隱藏層的神經網路，就是一個兩層神經網路。記住當我們算神經網路的層數時，我們不算輸入層，我們只算隱藏層和輸出層。

但是在過去的幾年中，DLI（深度學習學院 deep learning institute）已經意識到有一些函式，只有非常深的神經網路能學會，而更淺的模型則辦不到。儘管對於任何給定的問題很難去提前預測到底需要多深的神經網路，所以先去嘗試邏輯迴歸，嘗試一層然後兩層隱含層，然後把隱含層的數量看做是另一個可以自由選擇大小的超引數，然後再保留交叉驗證資料上評估，或者用你的開發集來評估。

我們再看下深度學習的符號定義：

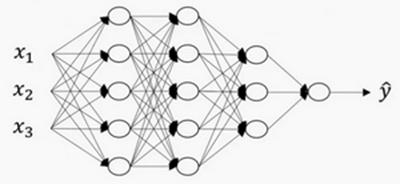
上圖是一個四層的神經網路，有三個隱藏層。我們可以看到，

第一層（即左邊數過去第二層，因為輸入層是第0層）有5個神經元數目，第二層5個，第三層3個。

我們用L表示層數，上圖：L=4，輸入層的索引為“0”，第一個隱藏層n^{([1])=5,表示有5個隱藏神經元，同理n}([2])=5，n^([3])=3，n([4])=n^{([L])=1（輸出單元為1）。而輸入層，n}([0])=n_x=3。

在不同層所擁有的神經元的數目，對於每層l都用a^{([l])來記作l層啟用後結果，我們會在後面看到在正向傳播時，最終能你會計算出a}([l])。

通過用啟用函式 g 計算z^{([l])，啟用函式也被索引為層數l，然後我們用w}

最後總結下符號約定：

輸入的特徵記作x，但是x同樣也是0層的啟用函式，所以x=a^([0])（你可以想象成輸入層就是一個啟用函式）。
最後一層的啟用函式，所以a^([L])是等於這個神經網路所預測的輸出結果。

前向傳播和反向傳播（Forward and backward propagation）

之前我們學習了構成深度神經網路的基本模組，比如每一層都有前向傳播步驟以及一個相反的反向傳播步驟，這次我們講講如何實現這些步驟。

先講前向傳播，輸入a^{([l-1])，輸出是a}([l])，快取為z^([l])；

從實現的角度來說我們可以快取下w^([l])和b([l])，這樣更容易在不同的環節中呼叫函式。

所以前向傳播的步驟可以寫成：

z^([l])=W([l])⋅a^([l])+b([l])

a^([l])=g([l]) (z^([l]) )

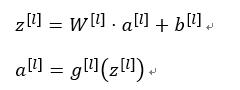
向量化實現過程可以寫成：

z^([l])=W([l])⋅A^([l-1])+b([l])

A^([l])=g([l]) (Z^([l]))

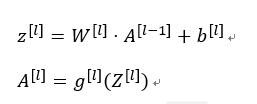
前向傳播需要喂入A^([0])也就是X（輸入特徵），來初始化；

初始化的是第一層的輸入值。a^([0])對應於一個訓練樣本的輸入特徵，

而A^([0])對應於一整個訓練樣本的輸入特徵，所以這就是這條鏈的第一個前向函式的輸入，重複這個步驟就可以從左到右計算前向傳播。

下面講反向傳播的步驟：

輸入為da^{([l])，輸出為da}([l-1])，dw^([l]), db^([l])

所以反向傳播的步驟可以寫成：

（1）dz^([l])=da([l])*g^([l])’(z([l]))

（2）dw^([l])=dz([l])⋅a^([l-1])

（3）db^([l])=dz([l])

（4）da^([l-1])=w[l]T⋅z^([l])

（5）dz^([l])=w([l+1]T) dz^([l+1])⋅ g^([l])’(z([l]))

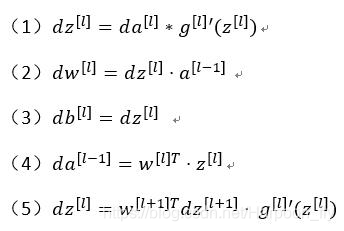
式子（5）由式子（4）帶入式子（1）得到，前四個式子就可實現反向函式。

向量化實現過程可以寫成：

（6）dZ^([l])=dA([l])*g¹ '(Z^([l]) )

（7）dW^([l])=1/m dZ^([l])⋅A[l-1]T

（8）db^([l])=1/m np.sum(dz^([l]),axis=1,keepdims=True)

（9）dA^([l-1])=W[l]T.dZ^([l])

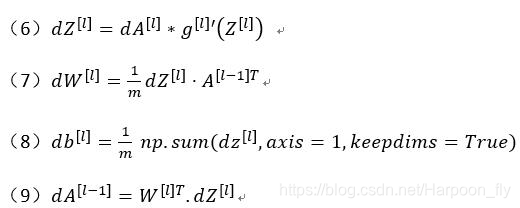
總結一下：

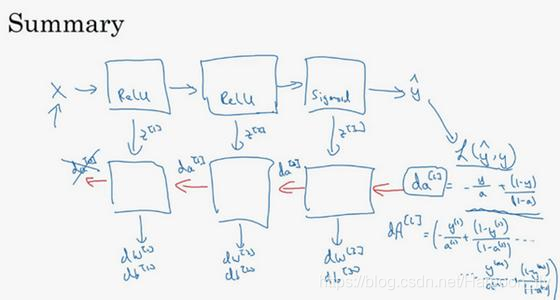
第一層你可能有一個ReLU啟用函式，

第二層為另一個ReLU啟用函式，

第三層可能是sigmoid函式（如果你做二分類的話），輸出值為y^，L(y, y)用來計算損失；這樣你就可以向後迭代進行反向傳播求導來求dw^([3])，db([3]) ，dw^([2]) ，db^([2]) ，dw^([1]) ，db^([1])。

在計算的時候，快取會把z^([1]) z^([2]) z^{([3])傳遞過來，然後回傳da}([2])，da^([1]) ，可以用來計算da^{([0])，但我們不會使用它，這裡講述了一個三層網路的前向和反向傳播，還有一個細節沒講就是前向遞迴——用輸入資料來初始化，那麼反向遞迴（使用Logistic迴歸做二分類）——對A}([l]) 求導。

上面可能有點晦澀難懂，猛地一看可能看不出什麼來，但是仔細看幾篇推導下還是有效果的，加油！

忠告：補補微積分和線性代數，多推導，多實踐。