2. 程式人生 > >用於CTC loss的幾種解碼方法：貪心搜尋 （greedy search）、束搜尋（Beam Search）、字首束搜尋（Prefix Beam Search）

用於CTC loss的幾種解碼方法：貪心搜尋 （greedy search）、束搜尋（Beam Search）、字首束搜尋（Prefix Beam Search）

阿新 • • 發佈：2018-12-09

在CTC網路中我們可以訓練出一個對映：

假如序列目標為字串（詞表大小為 n），則Nw輸出為n維多項概率分佈。

網路輸出為：y=Nw，其中，表示t時刻輸出是第k項的概率。

但是這個輸出只是一組組概率，我們要由這個Nw得到我們預測的標籤，這就涉及到一個解碼的問題。

 

按照最大似然準則，最優的解碼結果為： 

但是上式並不存在已知的高效解法。故我們可以採用下面介紹的幾種實用的近似破解碼方法。

在實際過程中難以計算，但對於某個具體的字串 π（去 blank 前），我們可以計算出：

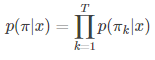
因此，我們放棄尋找使 最大的字串，而是尋找一個使最大的字串，即：

簡化後，解碼過程（構造）變得非常簡單（基於獨立性假設）： 在每個時刻t時輸出概率最大的字元：

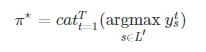
如：

假如y的分佈如下圖：

greedy search的結果為：

程式碼實現：

import numpy as np


# 求每一列(即每個時刻)中最大值對應的softmax值
def softmax(logits):
	# 注意這裡求e的次方時，次方數減去max_value其實不影響結果，因為最後可以化簡成教科書上softmax的定義
	# 次方數加入減max_value是因為e的x次方與x的極限(x趨於無窮)為無窮，很容易溢位，所以為了計算時不溢位，就加入減max_value項
	# 次方數減去max_value後，e的該次方數總是在0到1範圍內。
	max_value = np.max(logits, axis=1, keepdims=True)
	exp = np.exp(logits - max_value)
	exp_sum = np.sum(exp, axis=1, keepdims=True)
	dist = exp / exp_sum
	return dist


def remove_blank(labels, blank=0):
	new_labels = []
	# 合併相同的標籤
	previous = None
	for l in labels:
		if l != previous:
			new_labels.append(l)
			previous = l
	# 刪除blank
	new_labels = [l for l in new_labels if l != blank]

	return new_labels


def insert_blank(labels, blank=0):
	new_labels = [blank]
	for l in labels:
		new_labels += [l, blank]
	return new_labels


def greedy_decode(y, blank=0):
	# 按列取最大值，即每個時刻t上最大值對應的下標
	raw_rs = np.argmax(y, axis=1)
	# 移除blank,值為0的位置表示這個位置是blank
	rs = remove_blank(raw_rs, blank)
	return raw_rs, rs


np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
label_have_blank, label_no_blank = greedy_decode(y_test)
print(label_have_blank)
print(label_no_blank)

執行結果如下：

[1 3 5 5 5 5 1 5 3 4 4 3 0 4 5 0 3 1 3 3]
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3]

Process finished with exit code 0

貪心搜尋的效能非常受限。如它不能給出除最優路徑之外的其他其優路徑。很多時候，如果我們能拿到nearbest的路徑，後續可以利用其他資訊來進一步優化搜尋的結果。束搜尋能近似找出 top 最優的若干條路徑。

基本原理是通過  中 個序列，每個序列分別連線中個節點，得到 

個新序列及對應的score，然後按照score從大到小的順序選出前beamSize個序列，依次推進。

如：

假設為2,。

t=1時：

這個時候只會將兩個概率最大的節點放進路徑集合中，即有兩條路徑。

t=2時：

上面的兩個路徑每個路徑都會和下一個時間點的每一項組成新的路徑，因此一共有個新路徑。

然後我們還是隻保留概率最大的兩條路徑（次大的兩個路徑相等，這裡捨棄掉一個）。

t=3時：

和t=2時類似，又組成了新的6條路徑。我們還是取概率最大的兩條路徑。

實際使用該演算法時，往往取前20，這裡前2只是為了方便舉例。

程式碼實現：

import numpy as np


# 求每一列(即每個時刻)中最大值對應的softmax值
def softmax(logits):
	# 注意這裡求e的次方時，次方數減去max_value其實不影響結果，因為最後可以化簡成教科書上softmax的定義
	# 次方數加入減max_value是因為e的x次方與x的極限(x趨於無窮)為無窮，很容易溢位，所以為了計算時不溢位，就加入減max_value項
	# 次方數減去max_value後，e的該次方數總是在0到1範圍內。
	max_value = np.max(logits, axis=1, keepdims=True)
	exp = np.exp(logits - max_value)
	exp_sum = np.sum(exp, axis=1, keepdims=True)
	dist = exp / exp_sum
	return dist


def remove_blank(labels, blank=0):
	new_labels = []
	# 合併相同的標籤
	previous = None
	for l in labels:
		if l != previous:
			new_labels.append(l)
			previous = l
	# 刪除blank
	new_labels = [l for l in new_labels if l != blank]

	return new_labels


def insert_blank(labels, blank=0):
	new_labels = [blank]
	for l in labels:
		new_labels += [l, blank]
	return new_labels


def beam_decode(y, beam_size=10):
	# y是個二維陣列，記錄了所有時刻的所有項的概率
	T, V = y.shape
	# 將所有的y中值改為log是為了防止溢位，因為最後得到的p是y1..yn連乘，且yi都在0到1之間，可能會導致下溢位
	# 改成log(y)以後就變成連加了，這樣就防止了下溢位
	log_y = np.log(y)
	# 初始的beam
	beam = [([], 0)]
	# 遍歷所有時刻t
	for t in range(T):
		# 每個時刻先初始化一個new_beam
		new_beam = []
		# 遍歷beam
		for prefix, score in beam:
			# 對於一個時刻中的每一項(一共V項)
			for i in range(V):
				# 記錄新增的新項是這個時刻的第幾項，對應的概率(log形式的)加上新的這項log形式的概率(本來是乘的，改成log就是加)
				new_prefix = prefix + [i]
				new_score = score + log_y[t, i]
				# new_beam記錄了對於beam中某一項，將這個項分別加上新的時刻中的每一項後的概率
				new_beam.append((new_prefix, new_score))
		# 給new_beam按score排序
		new_beam.sort(key=lambda x: x[1], reverse=True)
		# beam即為new_beam中概率最大的beam_size個路徑
		beam = new_beam[:beam_size]

	return beam


np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
beam_chosen = beam_decode(y_test, beam_size=100)
for beam_string, beam_score in beam_chosen[:20]:
	print(remove_blank(beam_string), beam_score)

執行結果如下：

[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.261797539205567
[1, 3, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.279020152518033
[1, 3, 5, 1, 5, 3, 4, 2, 3, 4, 5, 3, 1, 3] -29.300726142201842
[1, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.310307014773972
[1, 3, 5, 1, 5, 3, 4, 2, 3, 3, 5, 3, 1, 3] -29.31794875551431
[1, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.327529628086438
[1, 3, 5, 1, 5, 4, 3, 4, 5, 3, 1, 3] -29.331572723457334
[1, 3, 5, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.33263180992451
[1, 3, 5, 4, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.334649090836038
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.33969505198154
[1, 3, 5, 2, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.339823066915415
[1, 3, 5, 1, 5, 4, 3, 3, 5, 3, 1, 3] -29.3487953367698
[1, 5, 1, 5, 3, 4, 2, 3, 4, 5, 3, 1, 3] -29.349235617770248
[1, 3, 5, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.349854423236977
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 3] -29.350803198551016
[1, 3, 5, 4, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.351871704148504
[1, 3, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.356917665294006
[1, 3, 5, 2, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.35704568022788
[1, 3, 5, 1, 5, 3, 4, 5, 4, 5, 3, 1, 3] -29.363802591012263
[1, 5, 1, 5, 3, 4, 2, 3, 3, 5, 3, 1, 3] -29.366458231082714

Process finished with exit code 0

可以看到log形式的score連加的結果都是負數，這是因為logx，當x屬於0到1之間時logx為負的。

束搜尋（Beam Search）存在的一個問題是，在儲存的 top N 條路徑中，可能存在多條實際上是同一結果（經過去重複、去 blank 操作後的）。這減少了搜尋結果的多樣性。字首束搜尋（Prefix Beam Search）方法，可以在搜尋過程中不斷的合併相同的字首。

probabilityWithBlank和probabilityNoBlank分別代表最後一個字元是空格和最後一個字元不是空格的概率。

如：

當t=2時，many-to-one map後為[1]的序列有三種：[1,0]，[0,1]，[1,1]，其中[1,0]是尾部帶blank的情況,[0,1]和[1,1]是尾部不帶blank的情況，那麼假設t=3時label為1，那麼新的序列就有以下幾種情況。

[1,0]+[1]=[1,0,1]->[1,0,1]

[0,1]+[1]=[0,1,1]->[1]

[1,1]+[1]=[1,1,1]->[1]

後兩者是新的尾部不為blank的序列,可見尾部不為blank在新序列產生的時候是可以算作一種情況的,這就是為什麼要分為blank和尾部不為blank的情況。

程式碼實現：

import numpy as np
from collections import defaultdict

ninf = float("-inf")


# 求每一列(即每個時刻)中最大值對應的softmax值
def softmax(logits):
	# 注意這裡求e的次方時，次方數減去max_value其實不影響結果，因為最後可以化簡成教科書上softmax的定義
	# 次方數加入減max_value是因為e的x次方與x的極限(x趨於無窮)為無窮，很容易溢位，所以為了計算時不溢位，就加入減max_value項
	# 次方數減去max_value後，e的該次方數總是在0到1範圍內。
	max_value = np.max(logits, axis=1, keepdims=True)
	exp = np.exp(logits - max_value)
	exp_sum = np.sum(exp, axis=1, keepdims=True)
	dist = exp / exp_sum
	return dist


def remove_blank(labels, blank=0):
	new_labels = []
	# 合併相同的標籤
	previous = None
	for l in labels:
		if l != previous:
			new_labels.append(l)
			previous = l
	# 刪除blank
	new_labels = [l for l in new_labels if l != blank]

	return new_labels


def insert_blank(labels, blank=0):
	new_labels = [blank]
	for l in labels:
		new_labels += [l, blank]
	return new_labels


def _logsumexp(a, b):
	'''
	np.log(np.exp(a) + np.exp(b))

	'''

	if a < b:
		a, b = b, a

	if b == ninf:
		return a
	else:
		return a + np.log(1 + np.exp(b - a))


def logsumexp(*args):
	'''
	from scipy.special import logsumexp
	logsumexp(args)
	'''
	res = args[0]
	for e in args[1:]:
		res = _logsumexp(res, e)
	return res


def prefix_beam_decode(y, beam_size=10, blank=0):
	T, V = y.shape
	log_y = np.log(y)
	# 最後一個字元是blank與最後一個字元為non-blank兩種情況
	beam = [(tuple(), (0, ninf))]
	# 對於每一個時刻t
	for t in range(T):
		# 當我使用普通的字典時，用法一般是dict={},新增元素的只需要dict[element] =value即可，呼叫的時候也是如此
		# dict[element] = xxx,但前提是element字典裡，如果不在字典裡就會報錯
		# defaultdict的作用是在於，當字典裡的key不存在但被查詢時，返回的不是keyError而是一個預設值
		# dict =defaultdict( factory_function)
		# 這個factory_function可以是list、set、str等等，作用是當key不存在時，返回的是工廠函式的預設值
		# 這裡就是(ninf, ninf)是預設值
		new_beam = defaultdict(lambda: (ninf, ninf))
		# 對於beam中的每一項
		for prefix, (p_b, p_nb) in beam:
			for i in range(V):
				# beam的每一項都加上時刻t中的每一項
				p = log_y[t, i]
				# 如果i中的這項是blank
				if i == blank:
					# 將這項直接加入路徑中
					new_p_b, new_p_nb = new_beam[prefix]
					new_p_b = logsumexp(new_p_b, p_b + p, p_nb + p)
					new_beam[prefix] = (new_p_b, new_p_nb)
					continue
				# 如果i中的這一項不是blank
				else:
					end_t = prefix[-1] if prefix else None
					# 判斷之前beam項中的最後一個元素和i的元素是不是一樣
					new_prefix = prefix + (i,)
					new_p_b, new_p_nb = new_beam[new_prefix]
					# 如果不一樣，則將i這項加入路徑中
					if i != end_t:
						new_p_nb = logsumexp(new_p_nb, p_b + p, p_nb + p)
					else:
						new_p_nb = logsumexp(new_p_nb, p_b + p)
					new_beam[new_prefix] = (new_p_b, new_p_nb)
					# 如果一樣，保留現有的路徑，但是概率上要加上新的這個i項的概率
					if i == end_t:
						new_p_b, new_p_nb = new_beam[prefix]
						new_p_nb = logsumexp(new_p_nb, p_nb + p)
						new_beam[prefix] = (new_p_b, new_p_nb)

		# 給新的beam排序並取前beam_size個
		beam = sorted(new_beam.items(), key=lambda x: logsumexp(*x[1]), reverse=True)
		beam = beam[:beam_size]

	return beam


np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
beam_test = prefix_beam_decode(y_test, beam_size=100)
for beam_string, beam_score in beam_test[:20]:
	print(remove_blank(beam_string), beam_score)

執行結果如下：

[1, 5, 4, 1, 3, 4, 5, 2, 3] (-18.189863809114193, -17.613677981426175)
[1, 5, 4, 5, 3, 4, 5, 2, 3] (-18.19636512622969, -17.621013424585406)
[1, 5, 4, 1, 3, 4, 5, 1, 3] (-18.31701896033153, -17.666629973270073)
[1, 5, 4, 5, 3, 4, 5, 1, 3] (-18.323388267369936, -17.674125139073176)
[1, 5, 4, 1, 3, 4, 3, 2, 3] (-18.415808498759556, -17.862744326248826)
[1, 5, 4, 1, 3, 4, 3, 5, 3] (-18.36642276663863, -17.898463479112884)
[1, 5, 4, 5, 3, 4, 3, 2, 3] (-18.42224294936932, -17.870025672291458)
[1, 5, 4, 5, 3, 4, 3, 5, 3] (-18.37219911390019, -17.905130493229173)
[1, 5, 4, 1, 3, 4, 5, 4, 3] (-18.457066311773847, -17.880630315602037)
[1, 5, 4, 5, 3, 4, 5, 4, 3] (-18.462614293487096, -17.88759583852546)
[1, 5, 4, 1, 3, 4, 5, 3, 2] (-18.458941701567706, -17.951422824358747)
[1, 5, 4, 5, 3, 4, 5, 3, 2] (-18.464527031120184, -17.958629487208658)
[1, 5, 4, 1, 3, 4, 3, 1, 3] (-18.540857550725587, -17.92058991009369)
[1, 5, 4, 5, 3, 4, 3, 1, 3] (-18.547146092248852, -17.928030266681613)
[1, 5, 4, 1, 3, 4, 5, 3, 2, 3] (-19.325467801462263, -17.6892032244089)
[1, 5, 4, 5, 3, 4, 5, 3, 2, 3] (-19.328748799764973, -17.694105969982637)
[1, 5, 4, 1, 3, 4, 5, 3, 4] (-18.79699026165903, -17.945090229238392)
[1, 5, 4, 5, 3, 4, 5, 3, 4] (-18.80358553427324, -17.95258394264377)
[1, 5, 4, 3, 4, 3, 5, 2, 3] (-19.18153184608281, -17.859420073785095)
[1, 5, 4, 1, 3, 4, 5, 2, 3, 2] (-19.4393492963852, -17.884502168470895)

Process finished with exit code 0

 

相關推薦

用於CTC loss的幾種解碼方法：貪心搜尋 （greedy search）、束搜尋（Beam Search）、字首束搜尋（Prefix Beam Search）

在CTC網路中我們可以訓練出一個對映： 假如序列目標為字串（詞表大小為 n），則Nw輸出為n維多項概率分佈。 網路輸出為：y=Nw，其中，表示t時刻輸出是第k項的概率。 但是這個輸出只是一組組概率，我們要由這個Nw得到我們預測的標籤，這就涉及到一個解碼的問題。 &nbs

分散式鎖的幾種實現方法：redis實現分散式鎖

使用失效的方式實現分散式鎖（推薦） import redis.clients.jedis.Jedis; /** * 使用redis實現分散式鎖（推薦） * */ public class JedLock { private static final String LOCK_KEY =

清除浮動的幾種簡單方法：萬能清除浮動法，clear:both......

方法一：給父級元素新增宣告：overflow:hidden;。 例： .wrap{ border:3px solid #000;overflow:hidden;} .box01{ width:500px; height:500px; background:#F

陣列的幾種合併方法：

1.concatvar arr1=[1,2,3]; var arr2=['a','b']; var arr3=[null,undefined]; var arr = arr1.concat(arr2,arr3); //合併一 var arr4=[['c','d'],3];

Android Toast幾種使用方法：附原始碼

Android Toast幾種使用方法： 一.預設展示： Toast toast=Toast.makeText(getApplicationContext(), "預設的Toast", Toast.LENGTH_SHORT); 解釋： (1).第一

學習筆記：幾種注入方法

//member template class Integer{ public: template <int N> void multiple(); private: int i_; }; template <> void Int

Chrome：inspect檢視android資料庫常用的幾種配置方法、chrome://inspect除錯工具離線包

目錄 前言 步驟： 總結： 前言 android比較常用的資料庫框架分別是：greendao、ormlite、realm，對於這三種資料庫的優缺點，既然你要使用了，就說明你有一定的瞭解，在這裡就不介紹了！如果需要可自行google搜尋即可。接下來

火狐瀏覽器如何js關閉窗口的幾種解決方法

div dom style itl 希望 mic rdquo nav 瀏覽器 今天在項目上有一個頁面要求在幾秒後自動關閉，想著還比較簡單，用window.close()就可以了，但是用IE/谷歌/火狐瀏覽器試了一下，發現IE可以，谷歌用網上的兼容方法也可以實現，但是火狐這裏

iOS 幾種加密方法

字符 shared 唯一性 append utf8 img ict nsh chain iOS常見的幾種加密方法 普通加密方法是講密碼進行加密後保存到用戶偏好設置中 鑰匙串是以明文形式保存，但是不知道存放的具體位置 一. base64加密 base64 編碼是現代密碼學的

Linux操作系統的幾種引導方法

Linux操作系統的幾種引導方法 方法1：引導軟盤 (1)在下用mkbootdisk制作。 (2)如果硬盤引導信息丟失，無法進入Linux系統做引導軟盤，對於RH，用RedHat 光盤引導進入secure模式，當詢問是否將硬盤中的linux系統設置為當前環境，選“是”，這時的系統進

多線程有幾種實現方法?同步有幾種實現方法?(被問到)

所有 正在 () read 異常 同步 -h 競爭 sync 多線程有兩種實現方法，分別是繼承Thread類與實現Runnable接口 同步的實現方面有兩種，分別是synchronized,wait與notify wait():使一個線程處於等待狀態，並且釋放所持有的對象的

html中設置錨點定位的幾種常見方法

element 針對 htm com script int nbsp onclick .get 1,使用id定位： <a href="#1F" name="1F">錨點1</a> <div name="1F"> <p>

字符串截取的幾種基本方法

字符串截取 clas mov logs reg -a expr body regex 分享幾個經常用到的字符串的截取 string str="123abc456";int i=3;1 取字符串的前i個字符 str=str.Substring(0,i); //

常見的幾種最優化方法（梯度下降法、牛頓法、擬牛頓法、共軛梯度法等）

linear 樣本 計算 每次 理學 系統 是否 底部 有效 我們每個人都會在我們的生活或者工作中遇到各種各樣的最優化問題，比如每個企業和個人都要考慮的一個問題“在一定成本下，如何使利潤最大化”等。最優化方法是一種數學方法，它是研究在給定約束之下如何尋求某些因素(的量)，以

清除浮動的幾種常用方法

src 添加 環繞 blog img eight 方式 內聯元素 特性 首先，浮動這個樣式的出現，僅僅只是為了實現圖文環繞的效果，現在大多時利用浮動來布局； 浮動： 　　使元素推理文檔流，按照指定方向發生移動； 　　遇到父級邊界或者相鄰的浮動元素會停下來； 浮動的特性： 　

SVN被鎖定的幾種解決方法

情況 ctr 點擊 tsd lean 一級目錄 svn 開啟 projects 用SVN經常出現被鎖定而無法提交的問題，選擇解鎖又提示沒有文件被鎖定，很是頭疼。 這裏整理了一下SVN 被鎖定的幾種解決方法： 1.出現這個問題後使用“清理”即"Clean up"功能，如果還

ASP.NET中彈出消息框的幾種常見方法

服務 復制代碼 添加 新的 警告 完成 方法 rip 最簡 在ASP.NET網站開發中，經常需要使用到alert消息框，尤其是在提交網頁的時候，往往需要在服務器端對數據進行檢驗，並給出提示或警告。 這裏，僅介紹幾種不同的實現方法。 1、眾所周知的方法是采用如下代碼來實現：

sql 的幾種常用方法

dataview 釋放資源 lose 總結 dap bool .sql res mar 第一個項目總結基類：database：主要是定義有關數據庫的方法: 1.打開數據庫 public static void Open() {

Java Script 腳本的幾種基本格式：

wrap javascrip 外部文件 text write scrip ace pre 基本 1、 <script> document.Write("Hello wrrld!!!"); </script> 2、 <scri

元素水平垂直居中的幾種常用方法

round IT spl translate 彈性 lex align mar con <!DOCTYPE html> <html> <head> <meta charset="UTF-8">