Leetcode題解系列——Count Complete Tree Nodes(c++版)
阿新 • • 發佈:2018-12-09
題目大意:統計一棵完全二叉樹的結點數
注意點:
- 完全二叉樹的性質:葉子結點只可能在該二叉樹最大的兩層上出現,而且結點先放滿左子樹再放右子樹。
- 使用直接掃描結點方法來統計,時間複雜度過高,顯然不適合。
- 要根據完全二叉樹的性質來設計演算法。
一.演算法設計
如何利用完全二叉樹的性質來進行統計呢?我們可以利用完全二叉樹的子樹仍然是完全二叉樹的性質來設計遞迴演算法,一層一層地往下統計。
我們先對根節點的左子樹以及右子樹都進行左深度統計。
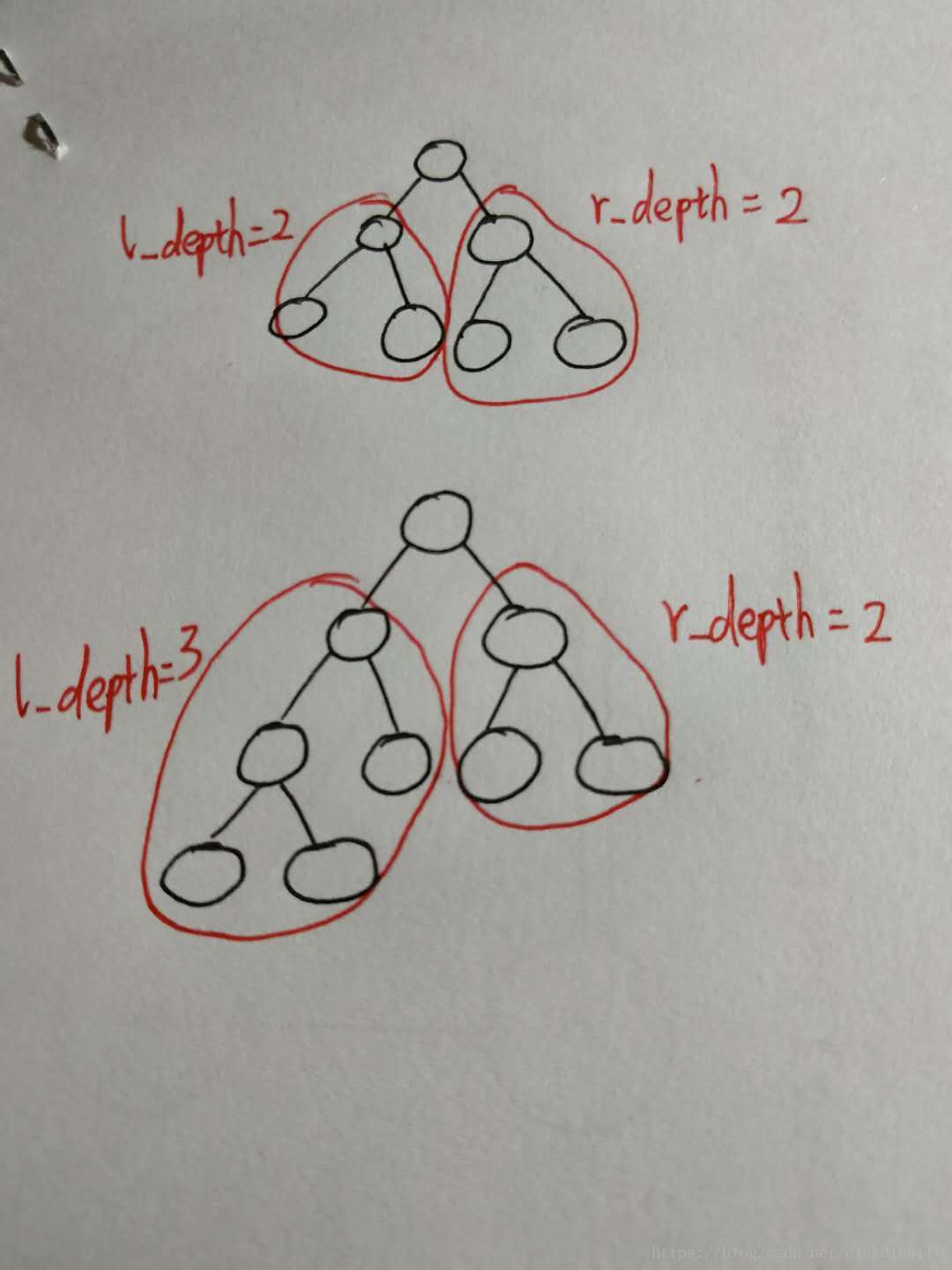
一棵完全二叉樹只有兩種情況,當左子樹的左深度等於右子樹的左深度,那麼左子樹一定是滿二叉樹;相反,當左子樹的左深度不等於右子樹的左深度,那麼右子樹一定是滿二叉樹。
如圖所示:
所以,我們可以根據這個性質來設計遞迴演算法,僅需要判斷左子樹與右子樹的左深度是否相同。
而一棵滿二叉樹的結點數為 , d為樹的深度。
二.實現程式碼
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public 三.從別人的程式碼中學習
在AC以後,當然少不了比較時間複雜度,結果發現可以寫出更好的程式碼。利用樹結點結構體有一個值的性質來直接遍歷,遍歷完成後修改該值,這算是比較巧妙的方法,當樹結點的值不能被修改時,實用性不是太好。當然,這只是一道演算法的題。
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == NULL) return 0;
if(root->val != -1){
root->val = -1;
return 1 + countNodes(root->left) + countNodes(root->right);
}
return 0;
}
};