C語言堆排序(HeapSort)的思想和程式碼實現

阿新 • • 發佈：2018-12-09

C語言堆排序(HeapSort)的思想和程式碼實現

經過一晚上和有一早上的思考和學習，在Clion上反覆的單步除錯之後，我總結了關於堆排序這個演算法的一點體會。現在來記錄一下,如有錯誤，歡迎批評指出，謝謝！

首先：什麼是堆排序，為什麼叫堆？

Heapsort是一種根據選擇排序的思想，利用堆這種資料結構 所設計的一種排序演算法

選擇排序的思想是什麼？：每一趟比較找到這個序列中的最值，拿出來和最前面的元素交換，交換完之後，這個序列從前面開始減去一個（因為前面放的是最值，不需要放在序列裡再次比較）

那麼這裡的堆是什麼意思呢？：堆是一個近似完全二叉樹的結構，並同時滿足堆積的性質：即子結點的鍵值或索引總是小於（或者大於）它的父節點。

什麼是完全二叉樹？即，每個節點都一一有序對應的滿二叉樹，如下圖所示

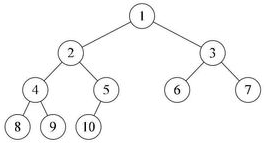
當一個序列滿足 雙親位置的值大於或者小於孩子位置的值的時候，就滿足堆的關係，（這裡為什麼要叫做位置？因為一般都是在序列裡面排序，儲存是線性的，比大根堆和小根堆如順序表）

#堆的種類，大根堆和小根堆

這個好理解，就是對應上面的圖來說，雙親位置的值大於孩子位置的值就是大根堆

雙親位置的值小於孩子位置的值就是小根堆

實現堆排序，我們需要解決什麼問題？

怎麼建立一個初始的堆？即滿足雙親位置的值大於或者小於孩子位置的值，我們只需要關注每一個雙親的孩子是不是大於或者小於自己孩子

，而不需要去管“別人家的孩子”是不是比自己家孩子大或者小
有了初始的堆之後，我們怎麼調整剩下的元素，這個時候就需要看看“別人家的孩子”，這樣處理之後，這個二叉樹就滿足完全二叉樹的特點，按照序列排列下來就是一個有序的序列

Part1：建立初始堆，我們要考慮什麼？

既然我們不需要去管整個序列是否有序，不需要去管“別人家的孩子”怎麼樣，那麼我們先要

找到所有雙親節點。

怎麼找呢？根據完全二叉樹的性質：

觀察每個雙親節點的序號，我們不難發現，他們的孩子節點的序號都是滿足：比如雙親節點是i，那麼他的左孩子就是2*i，右孩子就是2*i+1。

找到之後我們就開始調整每一個雙親位置的值和她的孩子的值：

我們這裡以建立一個小根堆為例子：

我們遍歷調整每個雙親節點的順序是：

從最大的雙親節點（非終端節點）（（整個順序表的長度）/2）一直倒著來，直到下標為1的根節點

為什麼是這個順序？為什麼不能倒著來？從1~length/2不是一樣的麼？

其實是不一樣的，我們建立小根堆的目的，就是為了將最小的交換到根節點，也就是說，最後調整完初始堆，

我們的根位置的值一定是整個序列中最小的值 —— 這是很重要的性質

我們從length/2開始對每個雙親位置進行堆的調整，那麼到了最後，最小的元素會出現在根位置

如果從1開始一直調整到length/2的雙親位置，那麼整個序列中最小的元素，不一定會出現在根位置，因為第一次調整之後根位置的值就不再變了，只是第一個雙親位置的最小的元素。

這裡有一個根據無序序列（62，25，49，25，16，8）建立小根堆的例子，順序如下

Part2：得到了初始小根堆，我們怎麼調整剩下的堆使得它有順序

根據前面提到的選擇排序的思想：

我們在這個heapsort裡面怎麼體現這種思想呢？

前面建立初始堆的時候，我們已經把最小的元素排出來，放在根位置了。那麼我們就相當於是拿到了選擇排序中的最值，這個時候我們只需要把他放在某個位置上之後，接下去就不再管它了，我們把它從序列中隔過去，在接下去的“找最值”的過程中把它忽視過去。這個“找最值”的過程就是上面Part 1 所說的，建立初始堆的過程。

我們這裡演算法的操作過程就是：

拿到最上面的根位置的值，和序列（長度n）最後一個元素交換位置。
然後把這個序列從後面縮小一個（序列長度n-1），也就是說，把剛剛那個元素隔過去
對剩下的這個被打亂的堆，再次進行Part 1的初始堆調整，我們還是想要得到剩下序列中最小的值

......（迴圈往復）直到這個序列的長度變成1 這個堆排序就執行完畢，得到了一個有序的序列。

還是上面那個（62....）的序列，我們從上面得到的小根堆開始調整到有序序列的例子

#到此為止，這個堆排序就算是理解完畢了，具體怎麼實現，在下面的程式碼中根據程式碼再次理解一次

1，建立順序表，由一個int陣列和一個指示長度的元素構成：

注意：這個陣列是從下標為1的地方開始儲存資料的！

#include "stdio.h"
#define Max_Num 100

typedef struct {
    int record[Max_Num];
    int length;
}OrderList;

2，還需要一個建立順序表的函式

這個比較簡單，也就是陣列的賦值，別忘了給長度的元素賦值

OrderList CreatOrderList(int n){
    int i;
    OrderList orderList;
    orderList.length = n;
    for(i=1;i<=n;i++){
        scanf("%d",&orderList.record[i]);
    }
    return orderList;
}

3，先簡單看一下main函式的呼叫結構吧

首先輸入長度，然後進入建立順序表的函式之後得到一個無序的順序表。

對這個順序表進行核心的堆排序操作，這裡傳送一個指標過去

然後我們把這個順序表輸出檢視一下就行，printOrderList這個函式的程式碼會在後面給出

int main( )
{
    int i,j;
    int n;
    printf("輸入序列長度");
    scanf("%d",&n);
    printf("輸入序列元素");

    OrderList orderList = CreatOrderList(n);
    HeapSort(&orderList);
    printOrderList(orderList);
    return 0;
}

4，最最最核心的堆排序程式碼部分

這個部分分成兩個函式，一個是 void HeapSort(OrderList *list)這個函式控制整個堆排序演算法的流程，也就是上面所說的part1，2

先建立初始堆，再遞迴調整剩餘堆的這樣兩個操作。

HeapAdjust(OrderList *list, int s, int m)這個函式功能就很清楚明白，對傳入的順序表，以及傳送的引數index（對應這次調整的開始位置），引數length（對應這次調整的順序表的長度）。HeapAdjust在整個流程中有兩種呼叫，一個是開始的建立初始堆，一個是後面的遞迴調整。

/**
 * 這個函式有兩個功能，一個是建立堆，一個是調整剩下節點
 * @param list
 * @param s
 * @param m
 */
void HeapAdjust(OrderList *list, int index, int length) {
    //儲存傳入節點的值
    int rc;
    int j;
    rc = list->record[index];
    for(j = 2*index;j<=length;j*=2){
        //如果左子樹（j=s*2）比右子樹j+1的大，說明右子樹更需要和雙親節點交換，則移動到record[j+1];
        if((j<length)&&(list->record[j]>list->record[j+1])){
            j++;  //下標移動
        }
        //如果孩子節點的值比雙親節點的值大，說明順序正確，不用交換，退出迴圈
        if(rc<list->record[j]){
            break;
        }
        //否則說明孩子節點值比雙親節點的小，交換
        list->record[index] = list->record[j];
        //如果換了，說明原來的雙親節點的數值被j的值覆蓋，
        //s的下標應該指向原來交換的地方（子節點）
        index = j;
    }
    //原來交換的地方（子節點）應該是原來雙親節點的值，之前被rc儲存，現在取出
    list->record[index] = rc;
}

void HeapSort(OrderList *list){
    int i;
    int temp;
    //迴圈第一次找到最後一個非葉子節點，迴圈下一次找到倒數第二個非葉子節點......
    for(i=list->length/2 ; i>0;--i){
        HeapAdjust(list,i,list->length);
    }
    /**
     * 把堆底元素和堆頂元素進行交換之後，刪除最後一個節點，對剩下的節點進行堆調整
     */
    for(i=list->length;i>1;--i){
        temp = list->record[1];
        list->record[1] = list->record[i];
        list->record[i] = temp;
        HeapAdjust(list,1,i-1);
    }
}

#完整程式碼如下:

包括順序表的建立，輸出，HeapSort和HeapAdjust

能實現的功能就是給定長度的順序表進行堆排序並輸出

#include "stdio.h"
#define Max_Num 100

typedef struct {
    int record[Max_Num];
    int length;
}OrderList;

void printOrderList(OrderList list){
    int i;
    for(i = 1;i<=list.length;i++){
        printf("%d ",list.record[i]);
    }
}
OrderList CreatOrderList(int n){
    int i;
    OrderList orderList;
    orderList.length = n;
    for(i=1;i<=n;i++){
        scanf("%d",&orderList.record[i]);
    }
    return orderList;
}

/**
 * 這個函式有兩個功能，一個是建立堆，一個是調整剩下節點
 * @param list
 * @param s
 * @param m
 */
void HeapAdjust(OrderList *list, int index, int length) {
    //儲存傳入節點的值
    int rc;
    int j;
    rc = list->record[index];
    for(j = 2*index;j<=length;j*=2){
        //如果左子樹（j=s*2）比右子樹j+1的大，說明右子樹更需要和雙親節點交換，則移動到record[j+1];
        if((j<length)&&(list->record[j]>list->record[j+1])){
            j++;  //下標移動
        }
        //如果孩子節點的值比雙親節點的值大，說明順序正確，不用交換，退出迴圈
        if(rc<list->record[j]){
            break;
        }
        //否則說明孩子節點值比雙親節點的小，交換
        list->record[index] = list->record[j];
        //如果換了，說明原來的雙親節點的數值被j的值覆蓋，
        //s的下標應該指向原來交換的地方（子節點）
        index = j;
    }
    //原來交換的地方（子節點）應該是原來雙親節點的值，之前被rc儲存，現在取出
    list->record[index] = rc;
}

void HeapSort(OrderList *list){
    int i;
    int temp;
    //迴圈第一次找到最後一個非葉子節點，迴圈下一次找到倒數第二個非葉子節點......
    for(i=list->length/2 ; i>0;--i){
        HeapAdjust(list,i,list->length);
    }
    /**
     * 把堆底元素和堆頂元素進行交換之後，刪除最後一個節點，對剩下的節點進行堆調整
     */
    for(i=list->length;i>1;--i){
        temp = list->record[1];
        list->record[1] = list->record[i];
        list->record[i] = temp;
        HeapAdjust(list,1,i-1);
    }
}

int main( )
{
    int i,j;
    int n;
    printf("輸入序列長度");
    scanf("%d",&n);
    printf("輸入序列元素");

    OrderList orderList = CreatOrderList(n);
    HeapSort(&orderList);
    printOrderList(orderList);
    return 0;
}

#總結：

這篇blog其實主要是是捋了捋堆排序的思路和實現過程，沒有闡述堆排的優缺點和應用之類的話題，接下去的複習應該多注意一下

2018年12月9日 14點07分

C語言堆排序(HeapSort)的思想和程式碼實現