題目來源：

題目描述：

題目描述

樹可以用來表示物種之間的進化關係。一棵“進化樹”是一個帶邊權的樹，其葉節點表示一個物種，兩個葉節點之間的距離表示兩個物種的差異。現在，一個重要的問題是，根據物種之間的距離，重構相應的“進化樹”。

令N={1..n}，用一個N上的矩陣M來定義樹T。其中，矩陣M滿足：對於任意的i，j，k，有M[i,j] + M[j,k] >= M[i,k]。樹T滿足：

1．葉節點屬於集合N；

2．邊權均為非負整數；

3．dT(i,j)=M[i,j]，其中dT(i,j)表示樹上i到j的最短路徑長度。

如下圖，矩陣M描述了一棵樹。

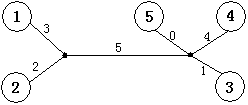
樹的重量是指樹上所有邊權之和。對於任意給出的合法矩陣M，它所能表示樹的重量是惟一確定的，不可能找到兩棵不同重量的樹，它們都符合矩陣M。你的任務就是，根據給出的矩陣M，計算M所表示樹的重量。下圖是上面給出的矩陣M所能表示的一棵樹，這棵樹的總重量為15。

輸入輸出格式

輸入格式：

輸入資料包含若干組資料。每組資料的第一行是一個整數n(2<n<30)。其後n-1行，給出的是矩陣M的一個上三角(不包含對角線)，矩陣中所有元素是不超過100的非負整數。輸入資料保證合法。

輸入資料以n=0結尾。

輸出格式：

對於每組輸入，輸出一行，一個整數，表示樹的重量。

輸入輸出樣例

輸入樣例#1： 複製

5
5 9 12 8
8 11 7
5 1
4
4
15 36 60
31 55
36
0

輸出樣例#1： 複製

15
71

解題思路：

     是一題思維題，考了樹的性質，我們可以考錄n=2的情況，那麼ans=dis（1，2），如果n=3，那麼3一定在1到2的邊上，那麼ans=dis（1，2）+len，len=（dis（1，3）+dis（3，2）-dis（1，2））/2，如果n>3我們可以列舉i，判斷n在那條邊上，分別計算len取最小的len加到答案裡面，就行。。

程式碼：

#include <iostream>
#include <cstring>
#include <string>
using namespace std;
int dis[35][35];
int js(int x,int y,int z)
{
    return (dis[x][z]+dis[y][z]-dis[x][y])/2;
}
int main()
{
    
    int n;
    while(cin>>n&&n)
    {
        memset(dis,0,sizeof(dis));
        for(int i=1;i<=n-1;i++)
        for(int j=i+1;j<=n;j++)
        {
            int a;
            cin>>a;
            dis[i][j]=dis[j][i]=a;
        }
        int ans=dis[1][2];
        for(int i=3;i<=n;i++)
        {
            int mixn=1e9;
            for(int j=1;j<i;j++)
            for(int k=j+1;k<i;k++)
            {
                if(mixn>js(j,k,i))mixn=js(j,k,i);
            }
            ans+=mixn;
        }
        cout<<ans<<endl;
    }
    
    return 0;
}