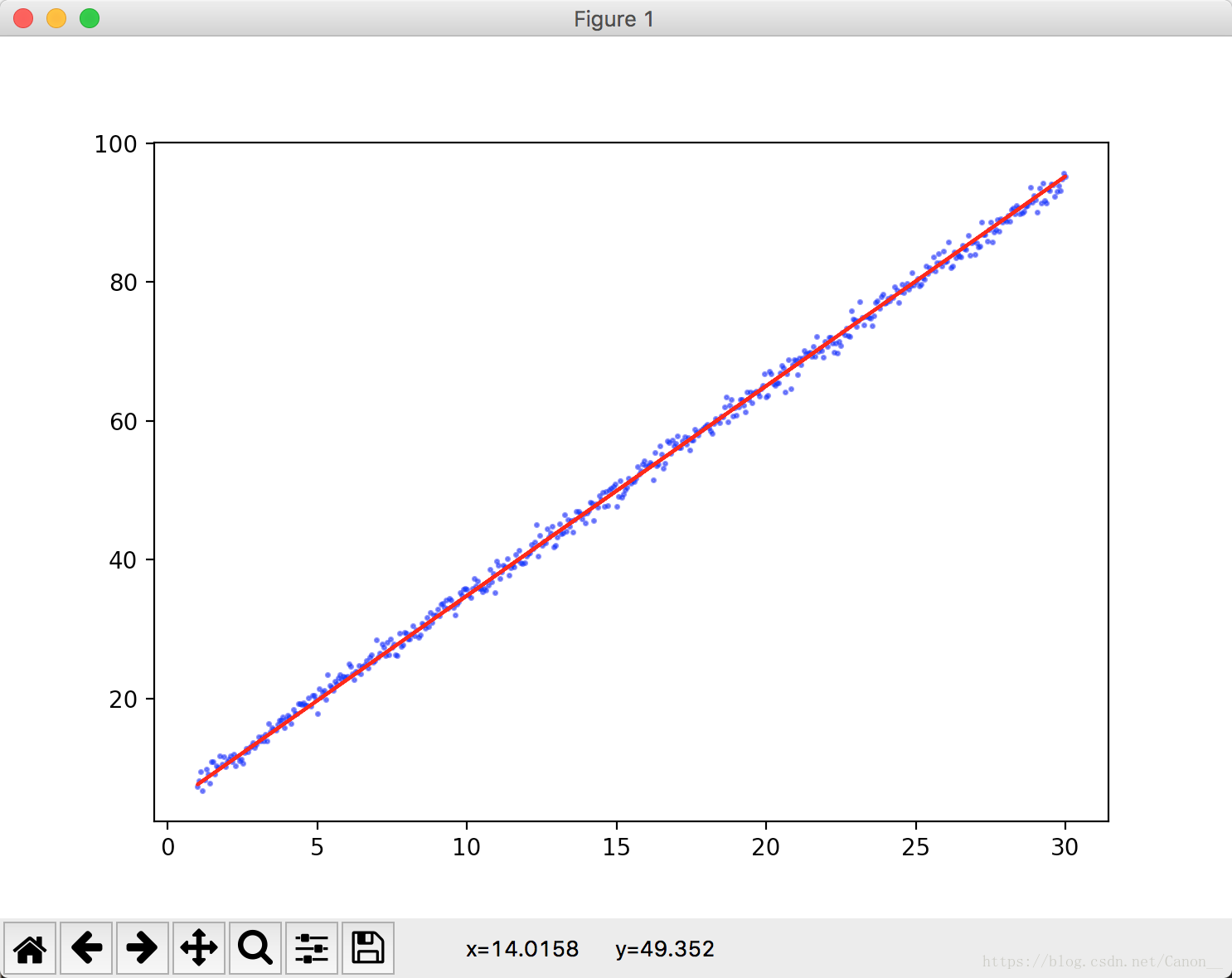
人們早就知道(並且找到了計算方法)，相比涼爽的天氣，在溫度較高的時候，蟋蟀鳴叫更為頻繁。這裡文件給出了我們圖片，我們拿一個直尺很容易就能畫一條線來近似這種關係。

雖然該直線並沒有精確的穿過每個點，但是我們還是能總結出大概的關係:

 y = w*x + b

這裡的 y 指預測標籤(我們預估的值)。

w指x的權重。

b指偏差。

x指特徵。

我們可以畫出無數條直線來預估這個圖片，哪一個效果最好呢？

我們通過loss(這裡用的均方誤差(MSE))函式，來最大限度的減少損失的模型，這一過程稱為  經驗風險最小化。

損失是一個數值，這個數值表示對單個樣本預測的精度，我們訓練模型的目標是一組樣本中平均損失“較小”的權重和偏差。

我們這裡只能找到平均損失較小(傳統神經網路存在區域性最優解的問題)的權重和偏差，至於原因，在以後會給出。

書中這裡給出了MSE的演算法，    (實際結果-預測結果)的平方和 再除以N,

這裡N為樣本總數。

雖然MSE演算法常見於機器學習，但它既不是唯一實用的損失函式，也不是適用於所有情形的最佳損失函式(特殊情況下，我們甚至

需要自己構建損失函式)。

習題答案:

1.均方誤差

對於兩張圖我們可以計算其均方誤差。

MSE(左側) =  (0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 +0^2 + 1^2 + 0^2 + 0^2)/10 = 2/5 = 0.4

MSE(右側) =  (0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2)/10 = 4/5 = 0.8

如果我們直接看殘差會發現兩者的殘差是相等的，就跟之前的《深入淺出的資料分析》中提到的類似，當時書中是用 RMSE來預估模型精度，我們這裡是用的MSE。

我這裡給出一個一元線性迴歸的例子(基於梯度下降法):

import numpy as np
import tensorflow as tf

x = np.linspace(1, 30, 500)[:, np.newaxis]
np.random.shuffle(x)
y = 3*x + 5 + np.random.standard_normal(500)[:, np.newaxis]

xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
weights = tf.Variable(tf.random_normal([1]))
biases = tf.Variable(tf.zeros(1) + 0.1)

wx_b = xs * weights + biases

loss = tf.reduce_mean(tf.square(wx_b - ys))

train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

for i in range(5000):
    sess.run(train_step, feed_dict={xs: x, ys: y})
    if i % 50 == 0:
        print(sess.run(loss, feed_dict={xs: x, ys: y}), sess.run(weights), sess.run(biases))


 

這裡的loss我使用的就是MSE,大家在訓練神經網路的時候，記得把資料打亂，這樣可以讓模型學習的更快速。我這裡用的np.random.shuffle 來打亂x的順序，並且給y加入了噪點。最終的執行結果MSE在1.06左右(每個人執行可能有偏差)。

我們可以在這裡匯入matlab模組來讓結果視覺化，這裡就不寫了，感興趣的可以自己動動手。