【機器學習】EM演算法在高斯混合模型學習中的應用

EM演算法，此部落格介紹了 $E M$ 演算法相關理論知識，看本篇部落格前先熟悉 $E M$ 演算法。

本篇部落格打算先從單個高斯分佈說起，然後推廣到多個高斯混合起來，最後給出高斯混合模型引數求解過程。

假如我們有一些資料，這些資料來自同一個高斯分佈（獨立同分布），那個我們如何根據這些資料估計出這個高斯分佈的引數呢？我們知道只要知道高斯分佈的引數 $θ = {μ, σ^{2}}$ 就能確定此高斯分佈。

從上圖中，我們要想知道資料是來自哪個高斯分佈，我們就要知道高斯分佈的引數，直觀上可以認定資料來自引數為

θ_{1}

的高斯分佈，然而這畢竟是我們直觀上的，那麼我們應該如何根據資料估計高斯分佈的引數呢？

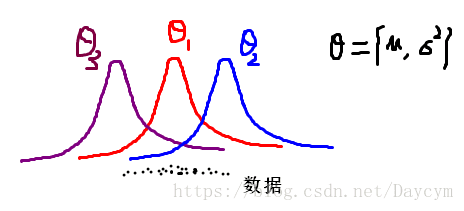
假設資料為 $X = {x_{1}, x_{2}, . . ., x_{N}} ， x_{i}$

X = {x_{1}, x_{2}, . . ., x_{N}} ， x_{i}

獨立同分布

p (X | θ)

，其中

θ = {μ, σ^{2}}

;

由貝葉斯公式知：

p (θ | X) \propto p (X | θ) p (θ)

p (θ | X)

為後驗概率，

p (X | θ)

為似然度，

p (θ)

為先驗概率。

關於貝葉斯公式的，可參考我之前的部落格，裡面有提到：連結

不加上先驗概率，就是極大似然估計；加上先驗概率，就是極大後驗概率估計這裡我們只介紹極大似然估計，極大後驗概率估計類似

（1）寫出對數似然函式

L (θ | X) = l o g [p (X | θ)] = \sum_{i = 1}^{N} l o g p (x_{i} | θ) = \sum_{i = 1}^{N} l o g [\frac{1}{\sqrt{2 π} σ} e x p (- \frac{(x_{i} - μ)^{2}}{2 σ^{2}})]

（2）求極大似然估計

分別對 $μ, σ$ 求偏導，並令為0：

\frac{\partial L (θ | X)}{\partial μ} = \frac{\partial (\sum_{i = 1}^{N} l o g [\frac{1}{\sqrt{2 π} σ} e x p (- \frac{(x_{i} - μ)^{2}}{2 σ^{2}})])}{\partial μ} = \frac{\partial (\sum_{i = 1}^{N} l o g [e x p (- \frac{(x_{i} - μ)^{2}}{2 σ^{2}})])}{\partial μ} = \frac{\partial (\sum_{i = 1}^{N} - \frac{(x_{i} - μ)^{2}}{2 σ^{2}})}{\partial μ} = - \sum_{i = 1}^{N} \frac{(x_{i} - μ)}{σ^{2}} = 0