構造雜湊表（散列表）以及二次探測法

今天做筆試題時，遇到一道構造雜湊表的題，hash函式是 k%11 ，然後一個數組記不清了，然後就是問二次探測法進行，問下面那個是正確，懵逼啊，沒做過，不知道，亂選直接下一題，於是有這個部落格，趕緊學習一波。

網上查詢了一下。

構造雜湊表的幾種方法

常用方法是直接定址法和除留餘數法

• 直接定址法（取關鍵字的某個線性函式為雜湊地址）

類似於這樣的式子

f(key) = a × key + b

• 除留餘數法（取關鍵值被某個不大於散列表長m的數p除後的所得的餘數為雜湊地址）

對於散列表長為m的雜湊函式公式為：

f( key ) = key mod p ( p ≤ m )

mod是取模（求餘數）的意思。事實上，這方法不僅可以對關鍵字直接取模，也可在摺疊、平方取中後再取模。

• 平方取中法

• 摺疊法

• 隨機數法

• 數學分析法

雜湊衝突（碰撞）以及處理

雜湊衝突：既然有雜湊函式Hash(key)，在有限的空間裡，肯定會產生相同的的值（雜湊地址），我們稱這種情況為雜湊衝突（碰撞）。任意的雜湊函式都不能避免產生衝突。

1. 開發定址法

所謂的開放定址法就是一旦發生了衝突，就去尋找下一個空的雜湊地址，只要散列表足夠大，空的雜湊地址總能找到，並將記錄存入。

• 線性探測法

fi(key) = (f(key)+di) MOD m (di=1,2,3,......,m-1)

用開放定址法解決衝突的做法是：當衝突發生時，使用某種探測技術在散列表中形成一個探測序列。沿此序列逐個單元地查詢，直到找到給定的關鍵字，或者碰到一個開放的地址（即該地址單元為空）為止（若要插入，在探查到開放的地址，則可將待插入的新結點存人該地址單元）。查詢時探測到開放的地址則表明表中無待查的關鍵字，即查詢失敗。

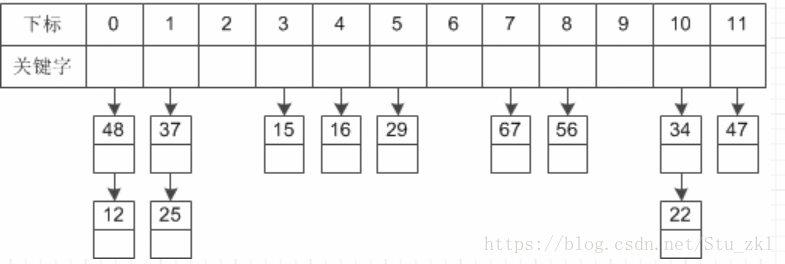
ep:我們的關鍵字集合為{12,67,56,16,25,37,22,29,15,47,48,34},表長為12。 我們用雜湊函式f(key) = key mod 12。

當計算前S個數{12,67,56,16,25}時，都是沒有衝突的雜湊地址，直接存入：

計算key = 37時，發現f(37) = 1，此時就與25所在的位置衝突。

於是我們應用上面的公式f(37) = (f(37)+1) mod 12 = 2。於是將37存入為2的下標位置。

接下來22,29,15,47都沒有衝突，正常的存入：

到了 key=48，我們計算得到f(48) = 0，與12所在的0位置衝突了，不要緊，我們f(48) = (f(48)+1) mod 12 = 1，此時又與25所在的位置衝突。於是f(48) = (f(48)+2) mod 12=2，還是衝突……一直到 f(48) = (f(48)+6) mod 12 = 6時，存入該位置：

我們把這種解決衝突的開放定址法稱為線性探測法。

• 二次探測法

考慮深一步，如果發生這樣的情況，當最後一個key=34，f(key)=10,與22所在的位置衝突，可是22後面沒有空位置了，反而它的前面有一個空位置，儘管可以 不斷地求餘數後得到結果，但效率很差。

因此我們可以改進di = 12, -12, 22, -22,……, q2, -q2 (q <= m/2),這樣就等於是可以雙向尋找到可能的空位置。

對於34來說，我 們取di即可找到空位置了。另外增加平方運算的目的是為了不讓關鍵字都聚集在 某一塊區域。我們稱這種方法為二次探測法。

f(key) = (f(key)+di) MOD m (di = 1^2, -1^2, 2^2, -2^2,……, q^2, -q^2, q <= m/2)

注：1^2 表示是 1的平方。

2. 鏈地址法

前面我們談到了雜湊衝突處理的開放定址法，它的思路就是一旦發生了衝突，就去尋找下一個空的雜湊地址。那麼，有衝突就非要換地方呢，我們直接就在原地處理行不行呢？

答案是可以的，就是鏈地址法，就好比Java裡的HashMap的資料結構一樣。