【機器學習】用QR分解求最小二乘法的最優閉式解

• 寫在前面
• QR分解
• 定義
• QR的求解
• 線性迴歸模型
• 用QR分解求解最優閉式解
• 矩陣的條件數
• 實驗
• 執行結果

寫在前面

今天刷知乎，看到張皓在面試官如何判斷面試者的機器學習水平？的回答裡面講到了關於用矩陣的QR分解求解最小二乘法閉式解的問題，碰巧前幾天《矩陣分析》課堂上剛講到QR分解，覺得挺有意思，值得深究，遂產生寫本篇博文的動機。另外本人知識水平理解能力有限，如有錯漏請各位大俠批評指正。

QR分解

先來看看維基百科上怎麼說:

QR分解法是三種將矩陣分解的方式之一。這種方式，把矩陣分解成一個半正交矩陣與一個上三角矩陣的積。QR分解經常用來解線性最小二乘法問題。QR分解也是特定特徵值演算法即QR演算法的基礎。

定義

實數矩陣的QR分解是把矩陣A分解為：

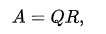
這裡的Q是正交矩陣（意味著Q^TQ = E）而R是上三角矩陣(即矩陣R的對角線下面的元素全為0)。為了便於理解，這裡引用一下daniel-D的圖：

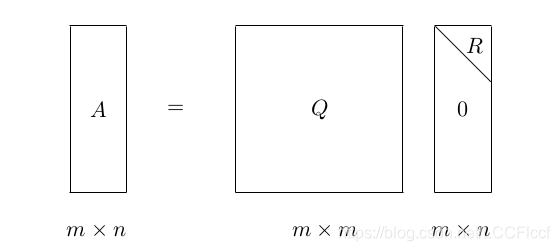
這個將A分解成這樣的矩陣Q和R的過程就是QR分解，QR分解可用於求解矩陣A的特徵值、A的逆等問題。具體參考血影雪夢大神的博文。

QR的求解

QR 分解的實際計算有很多方法，例如 Givens 旋轉、Householder 變換，以及 Gram-Schmidt 正交化等等。每一種方法都有其優點和不足。對於QR分解的求解這裡不再展開論述，在python中可以用numpy庫實現：

import numpy as np
Q, R = np.linalg.qr(A)

線性迴歸模型

給定資料集 $D=\left\{\right({\mathit{x}}_1,$

y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D=\{(\boldsymbol x_1,y_1),(\boldsymbol x_2,y_2),...,(\boldsymbol x_m,y_m)\} 其中 $\boldsymbol x_i=(x_{i1};x_{i2};...;x_{id}),y_i\in\mathbb R$.即樣本由 $d$個屬性描述。“線性迴歸”(linear regression)試圖學得一個線性模型以儘可能準確地預測實值輸出標記。
線性迴歸試圖學得的模型為： $f(\boldsymbol x_i)=\boldsymbol w^T\boldsymbol x_i+b, 使得f(\boldsymbol x_i)\simeq y_i$
這稱為“多元線性迴歸”(multivariate linear regression)
可以利用最小二乘法來對引數 $\boldsymbol w和b$進行估計。我們知道均方誤差是迴歸任務中最常用的效能度量，即通常所說的損失函式，這裡的損失函式可以表示為：
$J(\boldsymbol w,b)=\frac{1}{2} \sum_{i=1}^m (f(\boldsymbol x_i)-y_i)^2 = \frac{1}{2} \sum_{i=1}^m(y_i-\boldsymbol wx_i-b)^2$
因此我們可試圖讓均方誤差最小化，求出最優閉式解，即
$(\boldsymbol w^*,b^*) = \arg min_{(\boldsymbol w,b)} J(\boldsymbol w,b)$
在處理大型資料集時，我們一般都把引數和訓練資料進行向量化(vectorization)，即吸入矩陣中，再對矩陣進行計算，資料的向量化能給計算速度帶來非常大的提升。具體做法是：對於訓練引數，把 $\boldsymbol w和b吸收入向量形式\hat \boldsymbol w=(b; \boldsymbol w)$，即在列向量 $\boldsymbol w$的第一個元素前插入偏置項 $b$，此時的引數 $\hat \boldsymbol w$變成 $(d+1)\times 1$的列向量；即
$\hat \boldsymbol w= \begin{bmatrix} b \\ w_1 \\ \vdots \\ w_d \end{bmatrix}$
對於訓練資料集 $D$，我們把 $D$吸入一個 $m\times(d+1)$大小的矩陣 $\boldsymbol X$中，矩陣 $\boldsymbol X$的第一列用全為1的元素填充，即
$\left[\begin{array}{cccc}1& x_{11}& \cdots & x_{1d}\\ 1& x_{21}& \cdots & x_{2d}\\ \mathrm{⋮}& \mathrm{⋮}& \ddots & \mathrm{⋮}\\ 1& x_{m1}& \cdots & x_{md}\end{array}\right]=[\begin{array}{cc}1& {\mathit{x}}_1^T\\ 1& {\mathit{x}}_2^T\\ \mathrm{⋮}& \mathrm{⋮}\\ 1& \end{array}$