模型評估:模型狀態評估
模型狀態
過擬合和欠擬合
過擬合:在訓練集上的準確率較高,而在測試集上的準確率較低
欠擬合:在訓練集和測試集上的準確率均較低
學習曲線(Learning Curves)
1)概念概述
學習曲線就是通過畫出不同訓練集大小時訓練集和交叉驗證的準確率,可以看到模型在新資料上的表現,進而來判斷模型是否方差偏高或偏差過高,以及增大訓練集是否可以減小過擬合。
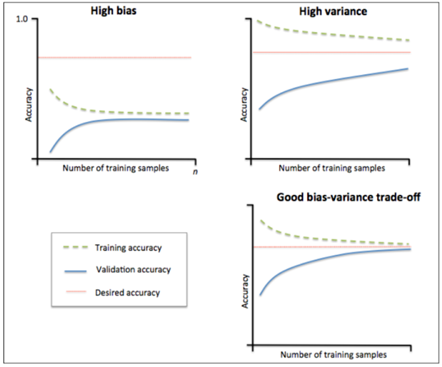
先明確兩個概念:
偏差:指的是分類器對訓練集和測試集的準確率與基準分類器的準確率有比較大的差距,是分類器與其他分類器的比較
方差:指的是分類器對訓練集的準確率和測試集的準確率有比較大的差距,是分類器自身的比較
當訓練集和測試集的準確率收斂且都收斂到較低準確率時,與基準分類器(紅線表示)相比為高偏差。
左上角表示分類器的偏差很高,訓練集和驗證集的準確率都很低,很可能是欠擬合。
我們可以增加模型引數,比如,構建更多的特徵,減小正則項。
此時通過增加資料量是不起作用的。
訓練集和測試集的準確率與基準分類器有差不多的準確率,說明偏差較低,但在測試集和訓練集的準確率差距較大,為高方差。
當訓練集的準確率比其他獨立資料集上的測試結果的準確率要高時,一般都是過擬合。
右上角方差很高,訓練集和驗證集的準確率相差太多,應該是過擬合。
我們可以增大訓練集,降低模型複雜度,增大正則項,或者通過特徵選擇減少特徵數。
理想情況是是找到偏差和方差都很小的情況,即收斂且誤差較小。
2)學習曲線的繪製:高偏差和高方差
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
#對於樸素貝葉斯,shape(train_sizes)=(1,5),shape(train_scores)=(5,100),shape(test_scores)=(5,100)
#對於支援向量機,shape(train_sizes)=(1,5),shape(train_scores)=(5,10),shape(test_scores)=(5,10)
train_sizes, train_scores, test_scores = learning_curve( estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
#顏色填充,寬度是2倍的標準差
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,test_scores_mean + test_scores_std, alpha=0.1, color="g")
#繪製折線圖
plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="Cross-validation score")
plt.legend(loc="best")
return plt
digits = load_digits()
X, y = digits.data, digits.target
#高偏差示例:樸素貝葉斯
title = "Learning Curves (Naive Bayes)"
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)
#高方差示例:SVM
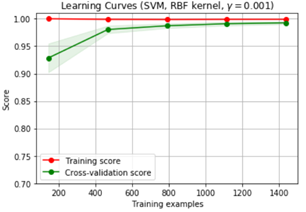
title = "Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
#定義交叉驗證
cv = ShuffleSplit(n_splits=15, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)
plt.show()