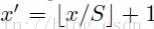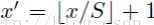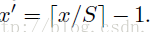作者：hjimce

一、相關理論

   本篇博文主要講解大神何凱明2014年的paper：《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition》，這篇paper主要的創新點在於提出了空間金字塔池化。paper主頁：http://research.microsoft.com/en-us/um/people/kahe/eccv14sppnet/index.html  這個演算法比R-CNN演算法的速度快了n多倍。

    我們知道在現有的CNN中，對於結構已經確定的網路，需要輸入一張固定大小的圖片，比如224*224，32*32,96*96等。這樣對於我們希望檢測各種大小的圖片的時候，需要經過裁剪，或者縮放等一系列操作，這樣往往會降低識別檢測的精度，於是paper提出了“空間金字塔池化”方法，這個演算法的牛逼之處，在於使得我們構建的網路，可以輸入任意大小的圖片，不需要經過裁剪縮放等操作，只要你喜歡，任意大小的圖片都可以。不僅如此，這個演算法用了以後，精度也會有所提高，總之一句話：牛逼哄哄。

    空間金字塔池化，又稱之為“SPP-Net”，記住這個名字，因為在以後的外文文獻中，你會經常遇到，特別是物體檢測方面的paper。這個就像什麼：OverFeat、GoogleNet、R-CNN、AlexNet……為了方便，學完這篇paper之後，你就需要記住SPP-Net是什麼東西了。空間金子塔以前在特徵學習、特徵表達的相關文獻中，看到過幾次這個演算法。

   既然之前的CNN要求輸入固定大小的圖片，那麼我們首先需要知道為什麼CNN需要輸入固定大小的圖片？CNN大體包含3部分，卷積、池化、全連線。

首先是卷積，卷積操作對圖片輸入的大小會有要求嗎？比如一個5*5的卷積核，我輸入的圖片是30*81的大小，可以得到(26,77)大小的圖片，並不會影響卷積操作。我輸入600*500，它還是照樣可以進行卷積，也就是卷積對圖片輸入大小沒有要求，只要你喜歡，任意大小的圖片進入，都可以進行卷積。

池化：池化對圖片大小會有要求嗎？比如我池化大小為（2，2）我輸入一張30*40的，那麼經過池化後可以得到15*20的圖片。輸入一張53*22大小的圖片，經過池化後，我可以得到26*11大小的圖片。因此池化這一步也沒對圖片大小有要求。只要你喜歡，輸入任意大小的圖片，都可以進行池化。

全連線層：既然池化和卷積都對輸入圖片大小沒有要求，那麼就只有全連線層對圖片結果又要求了。因為全連線層我們的連線勸值矩陣的大小W，經過訓練後，就是固定的大小了，比如我們從卷積到全連層，輸入和輸出的大小，分別是50、30個神經元，那麼我們的權值矩陣（50,30）大小的矩陣了。因此空間金字塔池化，要解決的就是從卷積層到全連線層之間的一個過度。

也就是說在以後的文獻中，一般空間金子塔池化層，都是放在卷積層到全連線層之間的一個網路層。

二、演算法概述

OK,接著我們即將要講解什麼是空間金字塔池化。我們先從空間金字塔特徵提取說起（這邊先不考慮“池化”），空間金字塔是很久以前的一種特徵提取方法，跟Sift、Hog等特徵息息相關。為了簡單起見，我們假設一個很簡單兩層網路：

輸入層：一張任意大小的圖片,假設其大小為(w,h)。

輸出層：21個神經元。

也就是我們輸入一張任意大小的特徵圖的時候，我們希望提取出21個特徵。空間金字塔特徵提取的過程如下：

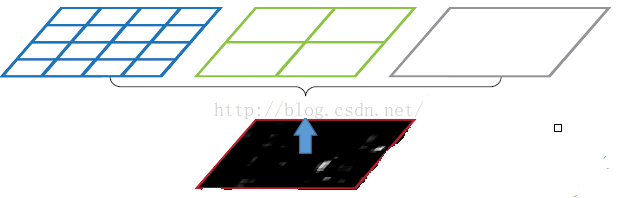
圖片尺度劃分

如上圖所示，當我們輸入一張圖片的時候，我們利用不同大小的刻度，對一張圖片進行了劃分。上面示意圖中，利用了三種不同大小的刻度，對一張輸入的圖片進行了劃分，最後總共可以得到16+4+1=21個塊，我們即將從這21個塊中，每個塊提取出一個特徵，這樣剛好就是我們要提取的21維特徵向量。

第一張圖片,我們把一張完整的圖片，分成了16個塊，也就是每個塊的大小就是(w/4,h/4);

第二張圖片，劃分了4個塊，每個塊的大小就是(w/2,h/2);

第三張圖片，把一整張圖片作為了一個塊，也就是塊的大小為(w,h)

空間金字塔最大池化的過程，其實就是從這21個圖片塊中，分別計算每個塊的最大值，從而得到一個輸出神經元。最後把一張任意大小的圖片轉換成了一個固定大小的21維特徵（當然你可以設計其它維數的輸出，增加金字塔的層數，或者改變劃分網格的大小）。上面的三種不同刻度的劃分，每一種刻度我們稱之為：金字塔的一層，每一個圖片塊大小我們稱之為：windows size了。如果你希望，金字塔的某一層輸出n*n個特徵，那麼你就要用windows size大小為：(w/n,h/n)進行池化了。

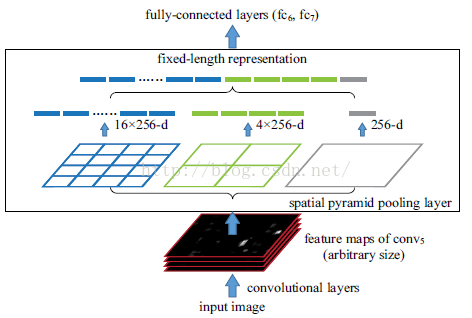
當我們有很多層網路的時候，當網路輸入的是一張任意大小的圖片，這個時候我們可以一直進行卷積、池化，直到網路的倒數幾層的時候，也就是我們即將與全連線層連線的時候，就要使用金字塔池化，使得任意大小的特徵圖都能夠轉換成固定大小的特徵向量，這就是空間金字塔池化的奧義（多尺度特徵提取出固定大小的特徵向量）。具體的流程圖如下：

三、演算法原始碼實現

 理論學的再多，終歸要實踐，實踐是檢驗理論的唯一標準，caffe中有關於空間金字塔池化的原始碼，我這邊就直接把它貼出來，以供學習使用，原始碼來自https://github.com/BVLC/caffe：

1. //1、輸入引數pyramid_level：表示金字塔的第幾層。我們將對這一層，進行劃分為2^n個圖片塊。金字塔從第0層開始算起，0層就是一整張圖片

2. //第1層就是把圖片劃分為2*2個塊，第2層把圖片劃分為4*4個塊，以此類推……，也就是說我們塊的大小就是[w/(2^n),h/(2^n)]

3. //2、引數bottom_w、bottom_h是我們要輸入這一層網路的特徵圖的大小

4. //3、引數spp_param是設定我們要進行池化的方法，比如最大池化、均值池化、概率池化……

5. LayerParameter SPPLayer<Dtype>::GetPoolingParam(const int pyramid_level,

6. const int bottom_h, const int bottom_w, const SPPParameter spp_param)

7. {

8. LayerParameter pooling_param;

9. int num_bins = pow(2, pyramid_level);//計算可以劃分多少個刻度，最後我們圖片塊的個數就是num_bins*num_bins

10. //計算垂直方向上可以劃分多少個刻度，不足的用pad補齊。然後我們最後每個圖片塊的大小就是(kernel_w,kernel_h)

11. int kernel_h = ceil(bottom_h / static_cast<double>(num_bins));//向上取整。採用pad補齊，pad的畫素都是0

12. int remainder_h = kernel_h * num_bins - bottom_h;

13. int pad_h = (remainder_h + 1) / 2;//上下兩邊分攤pad

14. //計算水平方向的刻度大小，不足的用pad補齊

15. int kernel_w = ceil(bottom_w / static_cast<double>(num_bins));

16. int remainder_w = kernel_w * num_bins - bottom_w;

17. int pad_w = (remainder_w + 1) / 2;

18. pooling_param.mutable_pooling_param()->set_pad_h(pad_h);

19. pooling_param.mutable_pooling_param()->set_pad_w(pad_w);

20. pooling_param.mutable_pooling_param()->set_kernel_h(kernel_h);

21. pooling_param.mutable_pooling_param()->set_kernel_w(kernel_w);

22. pooling_param.mutable_pooling_param()->set_stride_h(kernel_h);

23. pooling_param.mutable_pooling_param()->set_stride_w(kernel_w);

24. switch (spp_param.pool()) {

25. case SPPParameter_PoolMethod_MAX://視窗最大池化

26. pooling_param.mutable_pooling_param()->set_pool(

27. PoolingParameter_PoolMethod_MAX);

28. break;

29. case SPPParameter_PoolMethod_AVE://平均池化

30. pooling_param.mutable_pooling_param()->set_pool(

31. PoolingParameter_PoolMethod_AVE);

32. break;

33. case SPPParameter_PoolMethod_STOCHASTIC://隨機概率池化

34. pooling_param.mutable_pooling_param()->set_pool(

35. PoolingParameter_PoolMethod_STOCHASTIC);

36. break;

37. default:

38. LOG(FATAL) << "Unknown pooling method.";

39. }

40. return pooling_param;

41. }

42. template <typename Dtype>

43. //這個函式是為了獲取我們本層網路的輸入特徵圖、輸出相關引數，然後設定相關變數，比如輸入特徵圖的圖片的大小、個數

44. void SPPLayer<Dtype>::LayerSetUp(const vector<Blob<Dtype>*>& bottom,

45. const vector<Blob<Dtype>*>& top) {

46. SPPParameter spp_param = this->layer_param_.spp_param();

47. num_ = bottom[0]->num();//batch size 大小

48. channels_ = bottom[0]->channels();//特徵圖個數

49. bottom_h_ = bottom[0]->height();//特徵圖寬高

50. bottom_w_ = bottom[0]->width();

51. reshaped_first_time_ = false;

52. CHECK_GT(bottom_h_, 0) << "Input dimensions cannot be zero.";

53. CHECK_GT(bottom_w_, 0) << "Input dimensions cannot be zero.";

54. pyramid_height_ = spp_param.pyramid_height();//金子塔有多少層

55. split_top_vec_.clear();//清空相關資料

56. pooling_bottom_vecs_.clear();

57. pooling_layers_.clear();

58. pooling_top_vecs_.clear();

59. pooling_outputs_.clear();

60. flatten_layers_.clear();

61. flatten_top_vecs_.clear();

62. flatten_outputs_.clear();

63. concat_bottom_vec_.clear();

64. //如果金字塔只有一層，那麼我們其實是對一整張圖片進行pooling，也就是文獻所提到的：global pooling

65. if (pyramid_height_ == 1) {

66. // pooling layer setup

67. LayerParameter pooling_param = GetPoolingParam(0, bottom_h_, bottom_w_,spp_param);

68. pooling_layers_.push_back(shared_ptr<PoolingLayer<Dtype> > (new PoolingLayer<Dtype>(pooling_param)));

69. pooling_layers_[0]->SetUp(bottom, top);

70. return;

71. }

72. //這個將用於儲存金子塔每一層

73. for (int i = 0; i < pyramid_height_; i++) {

74. split_top_vec_.push_back(new Blob<Dtype>());

75. }

76. // split layer setup

77. LayerParameter split_param;

78. split_layer_.reset(new SplitLayer<Dtype>(split_param));

79. split_layer_->SetUp(bottom, split_top_vec_);

80. for (int i = 0; i < pyramid_height_; i++) {

81. // pooling layer input holders setup

82. pooling_bottom_vecs_.push_back(new vector<Blob<Dtype>*>);

83. pooling_bottom_vecs_[i]->push_back(split_top_vec_[i]);

84. pooling_outputs_.push_back(new Blob<Dtype>());

85. pooling_top_vecs_.push_back(new vector<Blob<Dtype>*>);

86. pooling_top_vecs_[i]->push_back(pooling_outputs_[i]);

87. // 獲取金字塔每一層相關引數

88. LayerParameter pooling_param = GetPoolingParam(i, bottom_h_, bottom_w_, spp_param);

89. pooling_layers_.push_back(shared_ptr<PoolingLayer<Dtype> > (new PoolingLayer<Dtype>(pooling_param)));

90. pooling_layers_[i]->SetUp(*pooling_bottom_vecs_[i], *pooling_top_vecs_[i]);

91. //每一層金字塔輸出向量

92. flatten_outputs_.push_back(new Blob<Dtype>());

93. flatten_top_vecs_.push_back(new vector<Blob<Dtype>*>);

94. flatten_top_vecs_[i]->push_back(flatten_outputs_[i]);

95. // flatten layer setup

96. LayerParameter flatten_param;

97. flatten_layers_.push_back(new FlattenLayer<Dtype>(flatten_param));

98. flatten_layers_[i]->SetUp(*pooling_top_vecs_[i], *flatten_top_vecs_[i]);

99. // concat layer input holders setup

100. concat_bottom_vec_.push_back(flatten_outputs_[i]);

101. }

102. // 把所有金字塔層的輸出，串聯成一個特徵向量

103. LayerParameter concat_param;

104. concat_layer_.reset(new ConcatLayer<Dtype>(concat_param));

105. concat_layer_->SetUp(concat_bottom_vec_, top);

106. }

函式GetPoolingParam是我們需要細讀的函式，裡面設定了金子塔每一層視窗大小的計算，其它的函式就不貼了，對caffe底層實現感興趣的，可以自己慢慢細讀。

四、演算法應用之物體檢測

在SPP-Net還沒出來之前，物體檢測效果最牛逼的應該是RCNN演算法了，下面跟大家簡單講一下R-CNN的總演算法流程，簡單回顧一下：

1、首先通過選擇性搜尋，對待檢測的圖片進行搜尋出2000個候選視窗。

2、把這2k個候選視窗的圖片都縮放到227*227，然後分別輸入CNN中，每個候選窗臺提取出一個特徵向量，也就是說利用CNN進行提取特徵向量。

3、把上面每個候選視窗的對應特徵向量，利用SVM演算法進行分類識別。

可以看到R-CNN計算量肯定很大，因為2k個候選視窗都要輸入到CNN中，分別進行特徵提取，計算量肯定不是一般的大。

OK，接著迴歸正題，如何利用SPP-Net進行物體檢測識別？具體演算法的大體流程如下：

1、首先通過選擇性搜尋，對待檢測的圖片進行搜尋出2000個候選視窗。這一步和R-CNN一樣。

2、特徵提取階段。這一步就是和R-CNN最大的區別了，同樣是用卷積神經網路進行特徵提取，但是SPP-Net用的是金字塔池化。這一步驟的具體操作如下：把整張待檢測的圖片，輸入CNN中，進行一次性特徵提取，得到feature maps，然後在feature maps中找到各個候選框的區域，再對各個候選框採用金字塔空間池化，提取出固定長度的特徵向量。而R-CNN輸入的是每個候選框，然後在進入CNN，因為SPP-Net只需要一次對整張圖片進行特徵提取，速度是大大地快啊。江湖傳說可一個提高100倍的速度，因為R-CNN就相當於遍歷一個CNN兩千次，而SPP-Net只需要遍歷1次。

3、最後一步也是和R-CNN一樣，採用SVM演算法進行特徵向量分類識別。

演算法細節說明：看完上面的步驟二，我們會有一個疑問，那就是如何在feature maps中找到原始圖片中候選框的對應區域？因為候選框是通過一整張原圖片進行檢測得到的，而feature maps的大小和原始圖片的大小是不同的，feature maps是經過原始圖片卷積、下采樣等一系列操作後得到的。那麼我們要如何在feature maps中找到對應的區域呢？這個答案可以在文獻中的最後面附錄中找到答案：APPENDIX A：Mapping a Window to Feature Maps。這個作者直接給出了一個很方便我們計算的公式：假設(x’,y’)表示特徵圖上的座標點，座標點(x,y)表示原輸入圖片上的點，那麼它們之間有如下轉換關係：

(x,y)=(S*x’,S*y’)

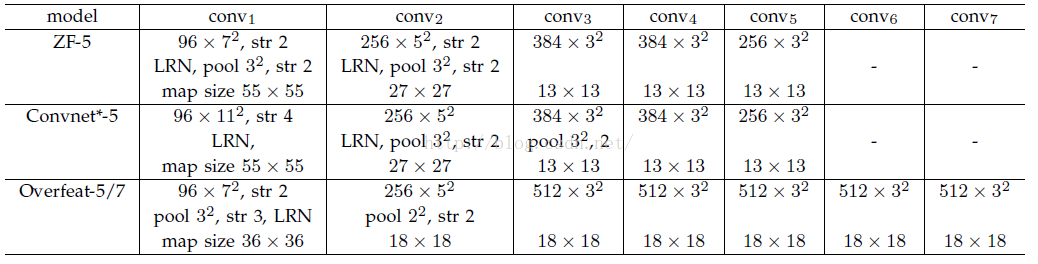
其中S的就是CNN中所有的strides的乘積。比如paper所用的ZF-5：

S=2*2*2*2=16

而對於Overfeat-5/7就是S=12，這個可以看一下下面的表格：

需要注意的是Strides包含了池化、卷積的stride。自己計算一下Overfeat-5/7(前5層)是不是等於12。

反過來，我們希望通過(x,y)座標求解(x’,y’)，那麼計算公式如下：

因此我們輸入原圖片檢測到的windows，可以得到每個矩形候選框的四個角點，然後我們再根據公式：

Left、Top:

Right、Bottom：

參考文獻：

2、《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition》

**********************作者：hjimce   時間：2015.12.5  聯絡QQ：1393852684   地址：http://blog.csdn.net/hjimce   原創文章，轉載請保留原文地址、作者等資訊****************