常用演算法總結

最近為了面試，在惡補演算法的一些知識，算是嚐到了大學沒有好好學習苦頭，博文是轉載的，我為了加深一些映像就自己寫一篇，順便加了一些自己的理解，有錯誤的話希望各位能夠指正。

排序演算法大體可分為兩種： 一種是比較排序，時間複雜度O(nlogn) ~ O(n^2)，主要有：氣泡排序，選擇排序，插入排序，歸併排序，堆排序，快速排序等。 另一種是非比較排序，時間複雜度可以達到O(n)，主要有：計數排序，基數排序，桶排序等。

這裡我們來探討一下常用的比較排序演算法，非比較排序演算法將在下一篇文章中介紹。下表給出了常見比較排序演算法的效能：

排序演算法穩定性的定義： 排序演算法穩定性的簡單形式化定義為：如果Ai = Aj，排序前Ai在Aj之前，排序後Ai還在Aj之前，則稱這種排序演算法是穩定的。通俗地講就是保證排序前後兩個相等的數的相對順序不變。 排序演算法穩定性的好處

氣泡排序

這個演算法就不用介紹了吧，基本每個初學者第一個接觸的演算法就是冒泡演算法，名字的由來就是沒經過一輪比較，最大或最小的數字就會像氣泡一樣浮到最尾段。 冒泡演算法的工作順序為： 1、比較相鄰的元素，如果需要調換位置的就進行調換 2、對每個元素重複步驟一，到最後一個元素將會是最大的元素 3、返回開始繼續重複上述的步驟，除了最後一個元素 4、繼續重複上述的步驟，直至沒有元素任何一對數字需要比較

// BubbleSort
void swap(int A, i, j) {
	int temp = A[i];
	A[i] = A[j];
	A[j] = temp;
}
void BubbleSort(int A, int n) {
	for(int i = 0; i < n-1; i++) {
		for(int j = 0; j < n-i-1; j++) { //每比完一輪，最大元素就浮到最後面，繼續比較浮完元素的前面元素
			if(A[j] > A[j+1]) {
				swap(A, j, j+1);
			}
		} 
	}
}
void mian() {
	int
 
 A[] = { 6, 5, 3, 1, 8, 7, 2, 4 };
	int n = sizeof(A) / sizeof(int);
	BubbleSort(A, n);
    printf("氣泡排序結果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
    return 0;
}

實現過程如下：

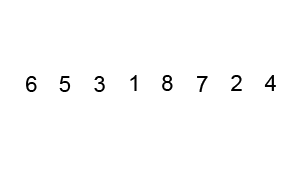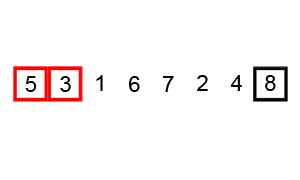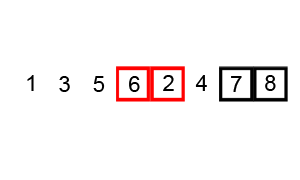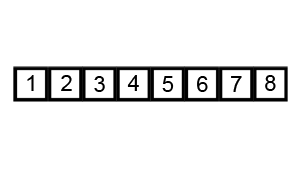
冒泡演算法的優點就是易於理解，但是是很沒有效率的演算法（如果一個數組有n個數，那麼排序完成後需要比較n*(n-1)/2次)

選擇排序

選擇排序也是一種簡單直觀的排序演算法。它的工作原理很容易理解：初始時在序列中找到最小（大）元素，放到序列的起始位置作為已排序序列；然後，再從剩餘未排序元素中繼續尋找最小（大）元素，放到已排序序列的末尾。以此類推，直到所有元素均排序完畢。 選擇排序跟氣泡排序最大區別在於：氣泡排序在遍歷的過程中重要符合條件都會進行交換，而選擇排序則在遍歷過程中記住了當前的最大或最小元素，才進行位置的交換

#include <stdio.h>

void swap(int A[], i, j) {
	int temp = A[i];
    A[i] = A[j];
    A[j] = temp;
}
void SelectSort(int A[], int n) {
	for(int i = 0; i < n-1; i++) {
		int min = i;
		for(int j = i+1; j < n-1; j++) {
			if(A[min] > A[j]) {
				min = j;
			}
		}
		if(min != i) {
			swap(A, min, i);
		}
	}
}
void mian() {
	int A[] = { 6, 5, 3, 1, 8, 7, 2, 4 };
	int n = sizeof(A) / sizeof(int);
	SelectSort(A, n);
    printf("氣泡排序結果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
    return 0;
}

選擇排序實現過程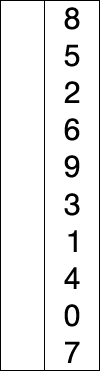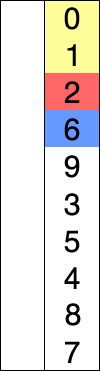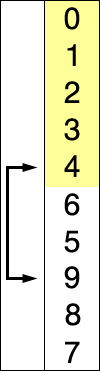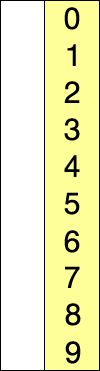： 選擇排序是不穩定的演算法： 比如序列：{ 5, 8, 5, 2, 9 }，第一次選擇的最小元素是2，然後把2和第一個5進行交換，從而改變了兩個元素5的相對次序。

插入排序

插入排序在實現上，通常採用in-place排序（即只需用到O(1)的額外空間的排序），因而在從後向前掃描過程中，需要反覆把已排序元素逐步向後挪位，為最新元素提供插入空間。插入排序的特點就是比較過的元素始終是排好序的。 具體演算法描述如下： 1、預設第一個元素是排好序的，從第二個元素開始進行向前比較 2、與上一個元素進行比較，如果比上一個元素小的話，則向前挪一位 3、重複步驟二，直到上一個元素比該元素小 4、將該元素插入到比較元素的後面 5、重複上述步驟，直到最後一個元素

#include <stdio.h>

void InsertionSort(int A[], int n) {
	for(int i = 1; i < n; i++) { //預設第一個元素是排好序的
		int right = A[i];
		int left = i - 1;
		while(j >= 0 && right < A[left]) { //當等於的時候不進入迴圈，因此插入排序是穩定的
			A[left] = A[left+1]; //如果右邊的元素比左邊的要小，就需要換位置
			left--;
		}
		A[left+1] = A[right]; //最後將元素插入到合適的位置中
	}
}
void main() {
	int A[] = { 6, 5, 3, 1, 8, 7, 2, 4 };// 從小到大插入排序
    int n = sizeof(A) / sizeof(int);
    InsertionSort(A, n);
    printf("插入排序結果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
    return 0;
}

上述程式碼對序列{ 6, 5, 3, 1, 8, 7, 2, 4 }進行插入排序的實現過程如下： 插入排序是穩定的演算法，在數量級較小的時候速度還是比較快的，但是當數量級多的時候，元素的移動會變得很費時間和效率。插入排序在工業級庫中也有著廣泛的應用，在STL的sort演算法和stdlib的qsort演算法中，都將插入排序作為快速排序的補充，用於少量元素的排序（通常為8個或以下）。

二分插入排序

因為插入排序前面比較過的元素始終是排序好的，所以後面的元素在查詢插入位置的時候可以用二分查詢，可以減少比較次數。

#include <stdio.h>
void InsertionSortDichotomy(int A[],  n) {
	for(int i = 1; i < n; i++) {
		int left = 0;
		int right = i-1;
		int ins = A[i];
		while(left <= right) {
			int mid = (left + right) / 2;
			if(A[mid] > ins) {
				right = mid - 1;
			} else {
				left = mid + 1;
			}
		}
		for(int j = right; j >= left; j--) {
			A[j+1] = a[j];
		}
		A[left] = ins;
	}
}
int main()
{
    int A[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 };// 從小到大二分插入排序
    int n = sizeof(A) / sizeof(int);
    InsertionSortDichotomy(A, n);
    printf("二分插入排序結果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
    return 0;
}

當n較大時，二分插入排序的比較次數比直接插入排序的最差情況好得多，但比直接插入排序的最好情況要差，所當以元素初始序列已經接近升序時，直接插入排序比二分插入排序比較次數少。二分插入排序元素移動次數與直接插入排序相同，依賴於元素初始序列。

快速排序

快速排序是由東尼·霍爾所發展的一種排序演算法。在平均狀況下，排序n個元素要O(nlogn)次比較。在最壞狀況下則需要O(n^2)次比較，但這種狀況並不常見。事實上，快速排序通常明顯比其他O(nlogn)演算法更快，因為它的內部迴圈可以在大部分的架構上很有效率地被實現出來。 快速排序使用分治策略(Divide and Conquer)來把一個序列分為兩個子序列。步驟為：

1、從序列中挑出一個元素，作為"基準"(pivot). 2、把所有比基準值小的元素放在基準前面，所有比基準值大的元素放在基準的後面（相同的數可以到任一邊），這個稱為分割槽(partition)操作。 3、對每個分割槽遞迴地進行步驟1~2，遞迴的結束條件是序列的大小是0或1，這時整體已經被排好序了。

#include <stdio.h>
void swap(int A[], i, j) {
	temp = A[i];
	A[i] = A[j];
	A[j] = temp;
}
void Partition(int A[], left, right) {
	int pivot = A[right]; //將最後一個元素假設為基準值
	int tail = left - 1;
	for(int i = left; i < right; i++) {
		if(A[i] <= pivot) {
			swap(A, ++tail, i);
		}
	}
	swap(A, ++tail, right);
	return tail;
}
void QuitSort(int A[], left, right) {
	if(left >= right) {
		return;
	}
	int pivot = Partition(A, left, right);
	QuitSort(A, left, pivot-1);
	QuitSort(A, pivit+1, right);
}
int main()
{
    int A[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 }; // 從小到大快速排序
    int n = sizeof(A) / sizeof(int);
    QuickSort(A, 0, n - 1);
    printf("快速排序結果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
    return 0;
}

快速排序是不穩定的排序演算法，不穩定發生在基準元素與A[tail+1]交換的時刻。 比如序列：{ 1, 3, 4, 2, 8, 9, 8, 7, 5 }，基準元素是5，一次劃分操作後5要和第一個8進行交換，從而改變了兩個元素8的相對次序。