常用排序演算法總結(Java實現)
阿新 • • 發佈:2018-12-23
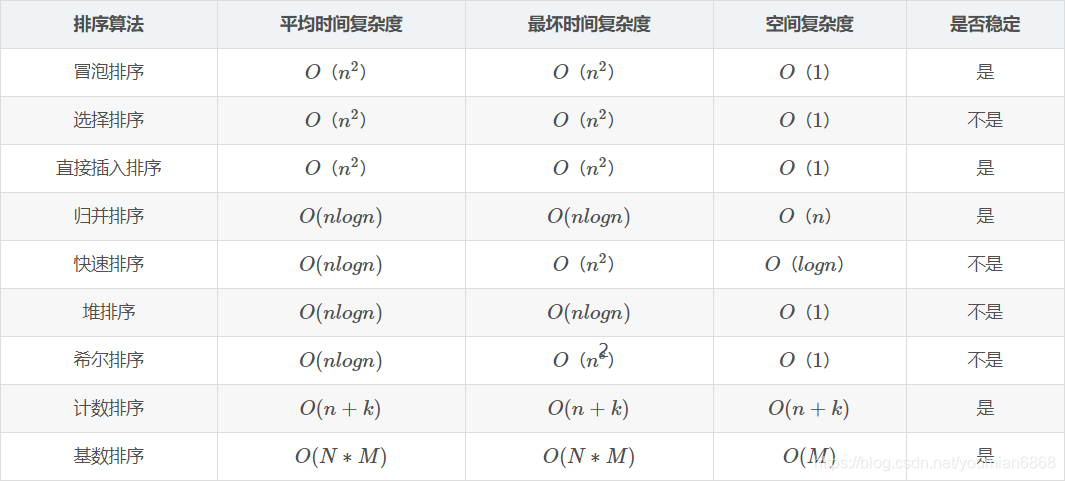
排序演算法比較:
1. 氣泡排序
/**
* 氣泡排序
* 比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
* 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。在這一點,最後的元素應該會是最大的數。
* 針對所有的元素重複以上的步驟,除了最後一個。
* 持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。
*
* @param array 需要排序的整型陣列
*/
public static void bubbleSort(int[] array) {
int temp = 0;
int len = array. 氣泡排序的改進:雞尾酒排序
/**
* 雞尾酒排序(氣泡排序的改進)
* 先找到最小的數字,把他放到第一位,然後找到最大的數字放到最後一位。
* 再找到第二小的數字放到第二位,再找到第二大的數字放到倒數第二位。
* 以此類推,直到完成排序。
*
* @param array 需要排序的整型陣列
*/
public static void cocktailSort(int[] array) {
int temp = 0;
int len = array.length;
for (int j = 0; j < len / 2; j++) {
//陣列中最大的數向右冒泡
for 2. 快速排序
/**
* 查找出中軸(預設是最低位start)的在陣列指定區間排序後所在位置
*
* @param array 待查詢陣列
* @param start 開始位置
* @param end 結束位置
* @return 中軸所在位置
*/
public static int partition(int[] array, int start, int end) {
int key = array[start]; //中軸通常設定為序列的第一項
while (start < end) {
while (start < end && array[end] >= key)
end--;
array[start] = array[end];
while (start < end && array[start] <= key)
start++;
array[end] = array[start];
}
array[start] = key;
return start;
}
/**
* 遞迴實現的快速排序
* 典型的分而治之思想
*
* @param array 待排序陣列
* @param start 開始位置
* @param end 結束位置
*/
public static void quickSort(int[] array, int start, int end) {
if (start < end) {
int index = partition(array, start, end);
quickSort(array, start, index - 1);
quickSort(array, index + 1, end);
}
}
3. 選擇排序
/**
* 選擇排序演算法
* 在未排序序列中找到最小元素,存放到排序序列的起始位置
* 再從剩餘未排序元素中繼續尋找最小元素,然後放到排序序列末尾。
* 以此類推,直到所有元素均排序完畢。
*
* @param array 需要排序的整型陣列
*/
public static void selectSort(int array[]) {
int len = array.length;
int temp = 0;
for (int i = 0; i < len - 1; i++) { //i為已排序序列的末尾
int min = i;
//找出未排序序列最小值所在的位置
for (int j = i + 1; j < len; j++) {
if (array[j] < array[min])
min = j;
}
temp = array[i];
array[i] = array[min];
array[min] = temp;
}
}
4. 插入排序
/**
* 插入排序
*
* 類似抓撲克牌排序
* 從第一個元素開始,該元素可以認為已經被排序
* 取出下一個元素,在已經排序的元素序列中從後向前掃描
* 如果該元素(已排序)大於新元素,將該元素移到下一位置
* 重複步驟3,直到找到已排序的元素小於或者等於新元素的位置
* 將新元素插入到該位置中
* 重複步驟2
*
* @param array 待排序陣列
*/
public static void insertSort(int[] array) {
int len = array.length;
int j, temp = 0;
for (int i = 1; i < len; i++) {
temp = array[i];
for (j = i; j > 0 && temp < array[j - 1]; j--) {
array[j] = array[j - 1];
}
array[j] = temp;
}
}
插入排序的改進:希爾排序
/**
* 希爾排序(插入排序的高效改進)
*
* 將整個有序序列分割成若干小的子序列分別進行插入排序。
*
* @param array 待排序陣列
*/
public static void shellSort(int[] array) {
int len = array.length;
int j, temp = 0;
int increment = len; //設定初始步長
while (true) {
increment /= 2; //每次將步長縮短為原來的一半
for (int x = 0; x < increment; x++) {
for (int i = x + increment; i < len; i += increment) {
temp = array[i];
for (j = i - increment; j >= 0 && array[j] > temp; j -= increment) {
array[j + increment] = array[j];
}
array[j + increment] = temp;
}
}
if (increment == 1)
break;
}
}
5.歸併排序
/**
* 歸併排序
*
* 將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。
* 然後再把有序子序列合併為整體有序序列。
*
* 時間複雜度為O(nlogn)
* 穩定排序方式
*
* @param array 待排序陣列
*/
public static void mergeSort(int[] array, int start, int end) {
int mid = (start + end) / 2;
if (start < end) {
mergeSort(array, start, mid);
mergeSort(array, mid + 1, end);
merge(array, start, mid, end);
}
}
/**
* 將陣列中low到high位置的數進行排序
*
* @param array 待排序陣列
* @param start 待排的開始位置
* @param mid 待排中間位置
* @param end 待排結束位置
*/
public static void merge(int[] array, int start, int mid, int end) {
int[] temp = new int[end - start + 1]; //輔助陣列
int i = start; //前一陣列的起始元素
int j = mid + 1; //後一陣列的起始元素
int k = 0;
//把較小的數先移到新陣列中
while (i <= mid && j <= end) {
if (array[i] <= array[j]) { //帶等號保證歸併排序的穩定性
temp[k++] = array[i++];
} else {
temp[k++] = array[j++];
}
}
//把左邊剩餘的數移入陣列
while (i <= mid) {
temp[k++] = array[i++];
}
//把右邊邊剩餘的數移入陣列
while (j <= end) {
temp[k++] = array[j++];
}
//把新陣列中的數覆蓋array陣列
for (k = 0; k < temp.length; k++) {
array[start + k] = temp[k];
}
}
6. 堆排序
/**
* 堆排序
*
* 由輸入的無序陣列構造一個最大堆,作為初始的無序區
* 把堆頂元素(最大值)和堆尾元素互換
* 把堆(無序區)的尺寸縮小1,並從新的堆頂元素開始進行堆調整
* 重複步驟2,直到堆的尺寸為1
*
* 時間複雜度為O(nlogn)
* 不穩定排序方式
*
* @param array 待排序陣列
*/
public static void heapSort(int[] array) {
int temp;
//構建大頂堆
for (int i = (array.length / 2) - 1; i >= 0; i--) { //從第一個非葉子結點從下至上,從右至左調整結構
adjustHeap(array, i, array.length);
}
//交換堆頂元素與末尾元素,並重新調整堆結構
for (int j = array.length - 1; j > 0; j--) {
temp = array[0];
array[0] = array[j];
array[j] = temp;
adjustHeap(array, 0, j);
}
}
/**
* 調整大頂堆
*
* @param array
* @param i
* @param length
*/
public static void adjustHeap(int[] array, int i, int length) {
int temp = array[i]; //取出當前元素值暫存
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) { //從i結點的左子結點開始
if (k + 1 < length && array[k] < array[k + 1]) { //如果左子結點小於右子結點,k指向右子結點
k++;
}
if (array[k] > temp) { //如果子節點大於起始元素,則將子節點值賦給父節點
array[i] = array[k];
i = k;
} else {
break;
}
}
array[i] = temp; //將起始元素值放到最終的位置
}
思考:
Java系統提供的Arrays.sort函式。對於基礎型別,底層使用快速排序。對於非基礎型別,底層使用歸併排序。請問是為什麼?
答:這是考慮到排序演算法的穩定性。對於基礎型別,相同值是無差別的,排序前後相同值的相對位置並不重要,所以選擇更為高效的快速排序,儘管它是不穩定的排序演算法;而對於非基礎型別,排序前後相等例項的相對位置不宜改變,所以選擇穩定的歸併排序。
