Problem Description

You are given array a of length n. You can choose one segment [l,r] (1≤l≤r≤n) and integer value k (positive, negative or even zero) and change al,al+1,…,ar by k each (i.e. ai:=ai+k for each l≤i≤r).

What is the maximum possible number of elements with value cc that can be obtained after one such operation?

Input

The first line contains two integers n and c (1≤n≤5⋅105, 1≤c≤5⋅105) — the length of array and the value c to obtain.

The second line contains nn integers a1,a2,…,an (1≤ai≤5⋅105) — array a.

Output

Print one integer — the maximum possible number of elements with value cc which can be obtained after performing operation described above.

Examples

Input

6 9
9 9 9 9 9 9

Output

6

Input

3 2
6 2 6

Output

2

————————————————————————————————————————————

題意：給出一長度為 n 的數列和一個數 c，能將一段連續區間裡的數都加上 k，使得整個序列中 c 儘可能的多，區間和 k 都由自己決定，求最多的個數

思路：學長說這個題是 DP，然後寫到自閉。。。

一開始想的是列舉 1~L 與 R~n 的區間，計算將他們變為 c 的個數，當前面的 c 的數量和後面的 c 的都已確定，再統計將中間出現次數最多的數都變成 c 的個數，但是寫到最後發現中間出現次數最多的數並不好計算。

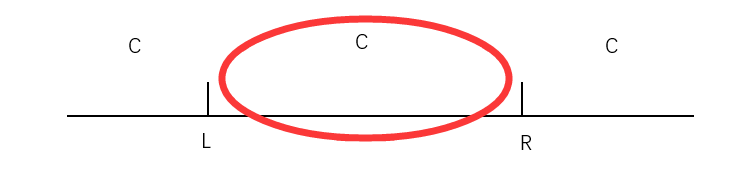
於是，可以從 1 開始列舉到某處 i，再加上 i 之後的數列中 c 的個數

用兩個陣列 up[i]、down[i] 分別儲存數列中從前向後、從後向前到 i 為止的等於 c 的個數

用 dp[i] 表示從前面某位置 pos 開始到現在位置 i，將 pos~i 之間出現次數最多的數變成 c、前 pos-1 個數最大的含 c 的數量

對於 pos 的位置，可以用一陣列 pre[x]=j 儲存，其表示對於某個數 a[i]==x，他上一次出現的位置是 j，即：a[j]=a[i]=x

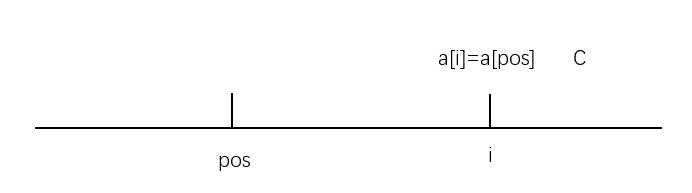
從而有了狀態轉移方程：

dp[i]=max(up[i-1]+1,dp[pre[a[i]]]+1);
pre[a[i]]=i;
ans=max(ans,dp[i]+down[i+1]);

從而保證從某個位置 pos 開始，dp[pos+1]~dp[i] 這一段出現次數最多的數變成了 c 的最大的

Source Program

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define PI acos(-1.0)
#define E 1e-6
#define MOD 16007
#define INF 0x3f3f3f3f
#define N 1000001
#define LL long long
using namespace std;
int a[N];
int up[N],down[N];
int dp[N];
int pre[N];
int main(){
    int n,c;
    cin>>n>>c;

    for(int i=1;i<=n;i++){
        cin>>a[i];
        up[i]=up[i-1]+(a[i]==c);
    }

    for(int i=n;i>=1;i--)
        down[i]=down[i+1]+(a[i]==c);

    int maxx=-INF;
    for(int i=1;i<=n;i++){
        dp[i]=max(up[i-1]+1,dp[pre[a[i]]]+1);
        pre[a[i]]=i;
        maxx=max(maxx,dp[i]+down[i+1]);
    }

    cout<<maxx<<endl;

    return 0;
}