C. NP-Hard Problem time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

Recently, Pari and Arya did some research about NP-Hard problems and they found the minimum vertex cover problem very interesting.

Suppose the graph G is given. Subset A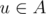

 of its vertices is called a vertex cover of this graph, if for each edge uv there is at least one endpoint of it in this set, i.e.  or  (or both).

Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.

They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A and B, such that both A and B are vertex cover or claim it's impossible. Each vertex should be given to no more than one of the friends (or you can even keep it for yourself).

Input

The first line of the input contains two integers n

 and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.

Each of the next m lines contains a pair of integers ui and vi (1  ≤  ui,  vi  ≤  n), denoting an undirected edge between ui and vi. It's guaranteed the graph won't contain any self-loops or multiple edges.

Output

If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).

If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integer k denoting the number of vertices in that vertex cover, and the second line contains kintegers — the indices of vertices. Note that because of m ≥ 1, vertex cover cannot be empty.

Examples input

4 2
1 2
2 3

output

1
2 
2
1 3 

input

3 3
1 2
2 3
1 3

output

-1

Note

In the first sample, you can give the vertex number 2 to Arya and vertices numbered 1 and 3 to Pari and keep vertex number 4 for yourself (or give it someone, if you wish).

In the second sample, there is no way to satisfy both Pari and Arya.

題意是要將一個圖的頂點分成兩個互不相交的子集，也就是說每一條邊的兩個頂點不能同時給一個人，需要把每條邊都切開。

給每個頂點都構建一個鄰接表，把該點先染為一種色，再把他所有的鄰接點都染為另一個色，跑完一輪bfs。每個點都需要先判斷一次是否已經被染色，若沒有則對其進行一輪染色，以此保證不是聯通圖也能把每個點都進行了染色。

#include <iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=1e5+5;
int h[M],cnt=0,c[M];

struct node
{
    int next,to;
}e[M*2];
void add(int u,int v)            //構建鄰接表
{
    e[cnt].to=v;
    e[cnt].next=h[u];
    h[u]=cnt++;
}
bool bfs(int s)
{
    c[s]=1;
    queue<int>q;
    q.push(s);
    while(!q.empty())                         
    {
        int x=q.front();
        q.pop();
        for(int i=h[x];i+1;i=e[i].next)                //對該點的所有鄰接點染色
        {
            int t=e[i].to;
            if(c[t]==-1)
            {
                c[t]=!c[x];
                q.push(t);
            }
            else if(c[x]==c[t]) return 1;
        }
    }
    return 0;
}
int main()
{
    int n,m,u,v;
    memset(h,-1,sizeof(h));
    memset(c,-1,sizeof(c));
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    for(int i=1;i<=n;i++)                //對每個點判斷是否被染色
    {
        if(c[i]==-1)
        {
            if(bfs(i))
            {
                puts("-1");
                return 0;
            }
        }
    }
    int aa=0,bb=0;
    int b[M],a[M];
    for(int i=1;i<=n;i++)
    {
        if(c[i]==1)
            b[bb++]=i;
        else
            a[aa++]=i;
    }
    printf("%d\n",aa);
    for(int i=0;i<aa;i++)
        printf("%d ",a[i]);
    printf("\n%d\n",bb);
    for(int i=0;i<bb;i++)
        printf("%d ",b[i]);
    printf("\n");
    return 0;
}