Chapter 1: Introduction 人類與環境進行互動，學習環境如何響應我們的行為，並試圖通過自身行為影響將來發生的事，這就是一種互動式的學習方式，是人類獲取知識的主要來源，同時也是幾乎所有學習和智慧化理論的基本思想。強化學習正是一種從互動中學習的計算方法，它更側重於從互動中進行目標導向的學習方式，而不是其他的機器學習方式。

1.1 Reinforcement Learning

強化學習特徵

強化學習就是學習該做什麼，如何將情境對映到動作從而最大化獎勵訊號。試錯搜尋（trial-and-error search）和延遲獎勵（delayed reward）是強化學習兩個最重要的顯著特徵，另一個重要特徵是強化學習並不侷限於孤立的子問題，即： · 學習者不會被告知需要採取哪些行動，而是必須通過嘗試來發現哪些行動可以產生最大的回報； · 當前行動不僅影響即時獎勵，還會影響下一個state，以及後續獎勵； · 明確考慮了目標導向的agent與不確定環境互動的整個問題。

強化學習與其他人工智慧技術的區別

監督學習：是從一組有標記的訓練集中進行學習，目的是讓系統歸納與推斷其響應，使其在訓練集中不存在的樣例下也能正確做出相應action。監督學習是一種重要的學習方式，但其不足以從互動中學習。在互動問題中獲取正確而又代表所有情況的所期望行為的樣例是不切實際的。在未知領域，agent必須能夠從自身經驗中學習才能習得最有益的action。

非監督學習：通常是尋找隱藏在未標記資料集合中的某種結構。雖然強化學習也不需要帶有正確標記的例子，但它的目標是最大化獎勵訊號，而不是試圖找到隱藏的結構。當然，找到agent學習經驗中的隱藏結構也是有用的，但這並不是最終目標。

強化學習的挑戰

探索與開發的權衡（trade-off between exploration and exploitation）。為了獲得大量獎勵，agent必須更傾向於過去嘗試過的行為，並且發現他們能夠有效地產生獎勵。但是要發現這樣的行為，agent必須嘗試以前沒有嘗試過的行為，它必須利用它已經經歷的經驗來獲得獎勵，但也必須進行探索，以便在將來做出更好的選擇。困難在於，任何探索和開發都有可能會失敗，agent必須嘗試各種操作，並逐漸傾向於那些看起來最好的操作。在隨機任務中，必須多次嘗試每一個action以獲得對其期望獎勵的可靠估計。

1.3 Elements of Reinforcement Learning

策略（policy）：策略定義了agent在給定時間內的行為方式。策略是從感知的環境狀態到該state下action的對映。通常策略可以是隨機的，指定每個action的概率。

獎勵訊號（reward signal）：獎勵訊號定義了強化學習問題的目標，是agent一次action後的反饋，說明了agent某個action對於目標而言是有利的還是有害的。獎勵訊號是更改策略的基礎，如果回報低，下次遇到相同的情況，agent就會採取不同的action。agent唯一的目標是最大化累計獲得的獎勵。

值函式（value function）：state的值表示agent以該state為起點，未來可期望的各個state回報的總和。獎勵訊號表示該state直接意義上的好壞，但值函式表示了以該state為起點，長期執行中的好壞。我們尋求的action應該是帶來最高value而非最高reward。

環境模型（model of the environment）：利用models來解決強化學習的方法為model-based method，反之叫做model-free method。對環境進行建模，不必在真實環境中試驗每一action，給定state和action，model會給出下一個state和返回的reward，極大減小了試錯搜尋的成本，是未來新的發展方向。

1.4 Limitations and Scope

進化方法（evolutionary methods）：如果策略空間較小，或可以被結構化（好的策略容易被檢索到），或者有大量時間可以用於搜尋，則進化方法是可行的。此外，進化方法在agent無法感知其環境的完整狀態的問題上具有優勢。

強化學習方法：進化方法（EM）只看policy的最後結果而不考慮中間的演變的過程。而強化學習方法在與環境的互動中學習，許多情況下，可以利用個體行為相互作用的細節。進化方法忽略了強化學習問題的許多有用結構：EM沒有利用所搜尋的policy是states到actions的對映這個事實；EM沒有注意到agent一生經過了哪些states，選擇了哪些actions。雖然某些情況下，該資訊可能具有誤導性（例如state被誤觀察），但更一般的，這些資訊會帶來更高效的搜尋。

1.5 An Extended Example: Tic-Tac-Toe

優化方法對比

以“井”字遊戲為例說明了傳統的AI方法如minimax、dynamic programming、evolutionary method都不太適合即使是這麼簡單的RL問題。

經典的博弈論的minimax解決方案在這裡是不正確的，因為它假定了對手的特定玩法。

用於順序決策問題的經典優化方法，例如dynamic programming，可以為任何對手計算最優解，但需要輸入該對手的完整規範，包括對手在每個棋盤狀態下進行每次移動的概率。

為了評估策略,進化方法使得策略固定並且針對對手玩許多次遊戲，或者使用對手的模型模擬許多次遊戲。勝利的頻率給出了對該策略獲勝概率的無偏估計，並且可用於指導下一個策略的選擇。但是每次策略更改都是在許多遊戲之後進行的，並且只使用每個遊戲的最終結果：在遊戲期間發生的事情會被忽略。例如，如果玩家獲勝，那麼遊戲中的所有行為都會被信任，而不管具體哪些actions對獲勝至關重要，甚至可以歸功於從未發生過的actions。

相反值函式方法允許評估各個states。最後，進化和值函式方法都在搜尋策略空間，但學習值函式會利用遊戲過程中可用的資訊。

value function方法步驟

1. 建立資料表，每個資料都代表遊戲中的一個可能state，每個數字都是我們從該state獲勝概率的最新估計；
2. 假設我們總是玩X，那麼連續三個X的value是1，連續三個O的value為0，其他狀態的初始值設定為0.5，表示我們有50％的獲勝機會；
3. 進行多場遊戲，大多數時候我們採用貪婪式方法，選擇導致具有最大value的state移動，即具有最高的估計獲勝概率。但偶爾也會採取隨機下法即探索性動作；
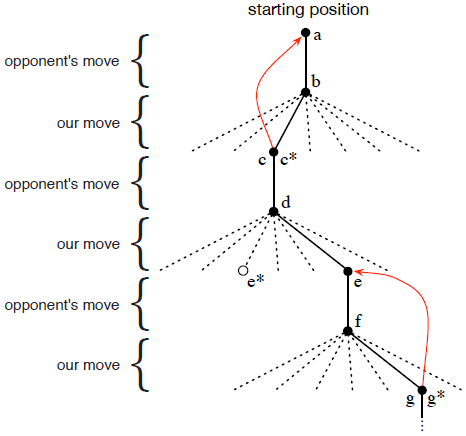
4. 在貪婪選擇時，使用時間差分法（temporal-di↵erence）更新之前state的value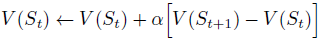： α為步長，S為state，V()為value。
5. 可以通過改變α慢慢趨向於0使得這個方法收斂到一個最優策略；也可以不改變α使得策略不斷改變以對抗對手。

擴充套件

本小節引出如下幾點思考：

1. 將先驗知識應用到強化學習中可以改善學習效果；
2. 強化學習的動作，除了像這個遊戲這種離散的，也可能是連續的，value函式也可能是連續函式；
3. 監督學習為程式提供了從其經驗中概括（泛化）的能力。因此當狀態集非常大甚至無限時，將監督學習方法與強化學習方法相結合是一個很好的解決途徑。ANN和DL並不是唯一的或最好的方法；
4. 如果能夠獲得或構建一個環境模型，則強化學習效果與效率會更好更高。

1.7 Early History of Reinforcement Learning

本小節講述了RL的三條研究主線：

1. learning with trial and error；
2. optimal control and its solution using value functions and dynamic programming(planning)；
3. TD-methods。

Exercise

Exercise 1.1：Self-Play Suppose, instead of playing against a random opponent, the reinforcement learning algorithm described above played against itself, with both sides learning. What do you think would happen in this case? Would it learn a different policy for selecting moves? 譯：假設上述強化學習演算法不是與隨機對手比賽，而是雙方都在學習。 在這種情況下你認為會發生什麼？ 是否會學習選擇行動的不同策略？ 答：對於固定的對手來說，演算法可能是次優的，對於隨機對手而言，演算法可能是最優的。對抗式學習和足夠的探索相較於一個固定的對手可以產生更為強大的智慧體。最後兩個智慧體應該會達到某種動態平衡，或是某方一直輸，另一方一直贏（初始動作或順序可能影響了學習策略）。

Exercise 1.2：Symmetries Many tic-tac-toe positions appear different but are really the same because of symmetries. How might we amend the learning process described above to take advantage of this? In what ways would this change improve the learning process? Now think again. Suppose the opponent did not take advantage of symmetries. In that case, should we? Is it true, then, that symmetrically equivalent positions should necessarily have the same value? 譯：許多井字位置看起來不同，但由於對稱性，它們實際上是相同的。我們如何修改上述學習過程以利用這一點？這種變化會以何種方式改善學習過程？ 現在再想一想。假設對手沒有利用對稱性。在那種情況下，我們應該嗎？那麼，對稱等價的位置是否必須具有相同的值？ 答：可以依據4個軸的對稱性對狀態空間進行約減，即對稱移動視為屬於相同的狀態空間，進而將減少實際的狀態數量，加速學習。如果對手沒有利用對稱性，則其策略會區分“對稱”狀態，這可能導致我們演算法整體效能變差。例如，如果對手在一個狀態空間中存在弱點但在另一個狀態空間中沒有（即使它們是對稱的），則對稱相似的狀態應該具有相同的值是不正確的，因此，這種情況下我們也不應該使用對稱性。

Exercise 1.3：Greedy Play Suppose the reinforcement learning player was greedy, that is, it always played the move that brought it to the position that it rated the best. Might it learn to play better, or worse, than a nongreedy player? What problems might occur? 譯：假設強化學習者是貪婪的，也就是說，它總是做出能夠把它帶到它認為最好的位置的動作。它可能會比一個不貪婪的學習者學的更好或更差嗎？可能會出現什麼問題？ 答：一般而言，貪婪玩家的學的可能會更差。貪婪玩家會追求最大的即時reward，而好的學習策略應該是追求最大的value，即累積回報。如果每一步都追求最好的動作，我們可能永遠找不到最優解。貪婪玩家可能會陷入區域性最優點。

Exercise 1.4：Learning from Exploration Suppose learning updates occurred after all moves, including exploratory moves. If the step-size parameter is appropriately reduced over time (but not the tendency to explore), then the state values would converge to a different set of probabilities. What (conceptually) are the two sets of probabilities computed when we do, and when we do not, learn from exploratory moves? Assuming that we do continue to make exploratory moves, which set of probabilities might be better to learn? Which would result in more wins? 譯：假設在所有動作之後發生了學習更新，包括探索性動作。 如果步長引數隨時間適當減小（但不是探索的趨勢），則狀態值將收斂到不同的概率集。 什麼（概念上）是我們這樣做時計算的兩組概率，當我們不這樣做時，從探索性動作中學習？ 假設我們繼續做出探索性的動作，哪一組概率可能更好學習？ 哪會贏得更多？ 答：一個狀態的值是從一個狀態開始直到獲勝的可能性。隨著步長的適當減少，且假設探索的概率是固定的，沒有從探索中學習的概率集是給定從此採取的最佳行動的每個狀態的值，而從探索中學習的概率集是包括主動探索策略在內的每個狀態的期望值。使用前者能夠更好地學習，因為它避免了演算法一味地進行貪婪式的行動，可能到達一個一般來說我們永遠不會到達的狀態，進而減少了次優的未來狀態的偏差（例如，如果你可以在一次移動中贏得一盤棋，但如果你執行另一次移動你的對手獲勝，這不會使該狀態變壞）。前者會在所有其他條件相同的情況下獲得更多勝利。

Exercise 1.5：1.5 Other Improvements Can you think of other ways to improve the reinforcement learning player? Can you think of any better way to solve the tic-tac-toe problem as posed? 譯：你能想到其他改善強化學習者的方法嗎？你能想出更好的方法來解決所提出的井字遊戲問題嗎？ 答：根據對手行為的變化改變探索率。加大損失的懲罰力度。

本部落格與https://xuyunkun.com同步更新

Reference: