在實際事例中，當一個隨機事件，例如某電話交換臺收到的呼叫、來到某公共汽車站的乘客、某放射性物質發射出的粒子、顯微鏡下某區域中的白血球等等，以固定的平均瞬時速率λ（或稱密度）隨機且獨立地出現時，那麼這個事件在單位時間（面積或體積）內出現的次數或個數就近似地服從泊松分佈P(λ)。因此,泊松分佈在管理科學、運籌學以及自然科學的某些問題中都佔有重要的地位。
泊松分佈適合於描述單位時間（或空間）內隨機事件發生的次數。如某一服務設施在一定時間內到達的人數，電話交換機接到呼叫的次數，汽車站臺的候客人數，機器出現的故障數，自然災害發生的次數，一塊產品上的缺陷數，顯微鏡下單位分割槽內的細菌分佈數等等。

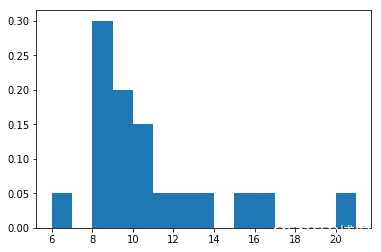
import numpy as np
import matplotlib.pyplot as plt
x=np.random.poisson(lam=10,size=20)
#lam:浮點數或類似陣列的浮點數。期望區間，應該是>= 0。一個期望間隔序列必須能夠在請求的大小上廣播。
print(x)
count, bins, ignored = plt.hist(x, 15, density=True)
plt.show()
 

[ 8 21 8 9 6 9 8 8 10 11 9 10 15 8 13 10 12 8 9 16]