線性代數的本質（七）——叉積

叉積的標準介紹

我們知道叉積的這個在學習線性代數的時候，我們知道，兩個向量做叉積運算會得出一個新的向量，新向量垂直於原兩個向量所在的平面，而且新向量的長度是原兩個向量所圍成的面積大小。

$\vec{a} \times \vec{b} = \det \left( \begin{bmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{bmatrix} \right) = \det \left( \begin{bmatrix} \hat{i} & a_x & b_x \\ \hat{j} & a_y & b_y \\ \hat{k} & a_z & b_z \end{bmatrix} \right)$

$a \times b = det ⎝ ⎛ ⎣ ⎡ \hat{i} a_{x} b_{x} \hat{j} a_{y} b_{y} \hat{k} a_{z} b_{z} ⎦ ⎤ ⎠ ⎞ = det ⎝ ⎛ ⎣ ⎡ \hat{i} \hat{j} \hat{k} a_{x} a_{y} a_{z} b_{x} b_{y} b_{z} ⎦ ⎤ ⎠ ⎞$

$\left| \vec{a} \times \vec{b} \right| = |\vec{a}| \times |\vec{b}| \times \sin(\theta)$

$\theta$ 是兩個向量 $\vec{a}$ 和向量 $\vec{b}$ 的夾角

在這裡插入圖片描述

由於這裡涉及到了兩個向量圍成的面積，所以在前面講到的行列式能在這裡起到作用。

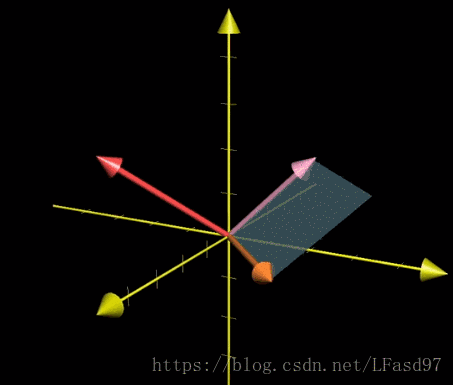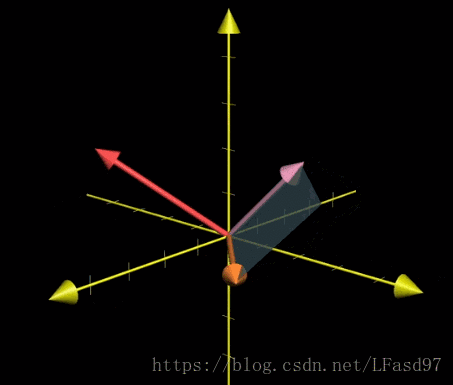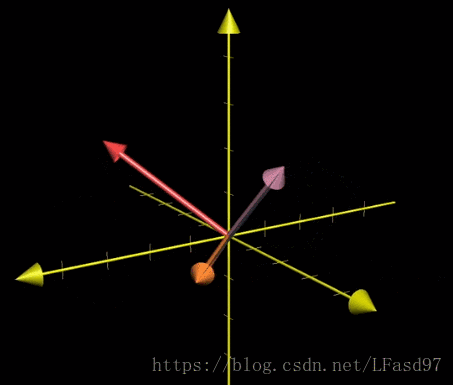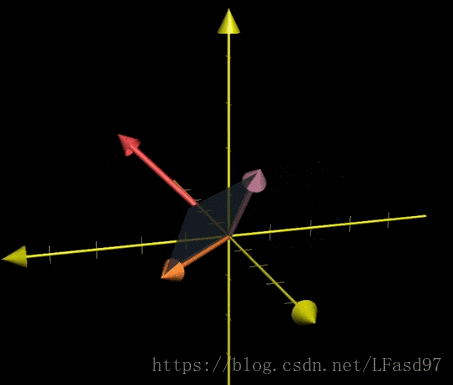
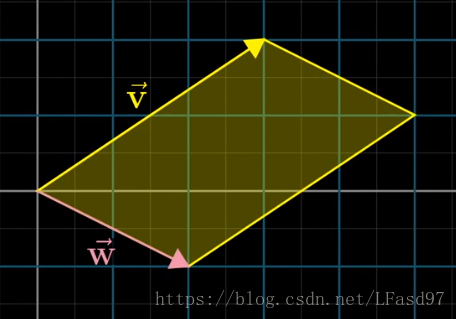
在這裡插入圖片描述

我們以上面這個圖片為例，向量 $\vec{v}$ 和向量 $\vec{w}$ 做叉積得出向量的長度可以使用行列式來計算，由於這裡只有兩個向量，所以我們回到二維空間中進行計算，由於垂直於向量 $\vec{v}$ 和向量 $\vec{w}$ 所圍成的平面有兩個方向，可以使用行列式裡面學過的 $\vec{v}$ 在 $\vec{w}$ 的左邊還是右邊來判斷，如下面的式子。

$\det \left( \begin{bmatrix} v_1 & w_1 \\ v_2 & w_2 \end{bmatrix} \right) = -\det \left( \begin{bmatrix} w_1 & v_1 \\ w_2 & v_2 \end{bmatrix} \right)$

$det ([v_{1} v_{2} w_{1} w_{2}]) = - det ([w_{1} w_{2} v_{1} v_{2}])$

也可以直接在三維空間中使用左手右手定則來判斷新向量指向的方向。跟前面行列式介紹的左右手定則基本一樣。這裡只列出右手定則

在這裡插入圖片描述

以線性變換的眼光看叉積

我們看到最上面的叉積的公式

$\vec{a} \times \vec{b} = \det \left( \begin{bmatrix} \hat{i} & a_x & b_x \\ \hat{j} & a_y & b_y \\ \hat{k} & a_z & b_z \end{bmatrix} \right) = \hat{i}(a_yb_z - a_zb_y) + \hat{j}(a_zb_x-a_xb_z) + \hat{k}(a_xb_y - a_yb_x)$

這個公式是怎麼來的，為什麼會把單位向量放到矩陣裡面計算行列式，為什麼向量叉積的結果是一個長度等於原來兩個向量圍成的面積？

我們知道，一個 $3 \times 3$ 矩陣的行列式的幾何意義是空間六面體的體積，而上面行列式的出來的結果是一個向量，是由於我們把單位向量作為矩陣單元。我們首先將 $\vec{a} \times \vec{b}$ 轉換成 $\vec{p} = \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix}$ ，然後上面的公式就改寫成下面的樣子。

$p_x\hat{i} + p_y\hat{j} + p_z\hat{k} = \det \left( \begin{bmatrix} \hat{i} & a_x & b_x \\ \hat{j} & a_y & b_y \\ \hat{k} & a_z & b_z \end{bmatrix} \right) = \hat{i}(a_yb_z - a_zb_y) + \hat{j}(a_zb_x-a_xb_z) + \hat{k}(a_xb_y - a_yb_x)$

相關推薦

線性代數的本質（七）——叉積

叉積的標準介紹我們知道叉積的這個在學習線性代數的時候，我們知道，兩個向量做叉積運算會得出一個新的向量，新向量垂直於原兩個向量所在的平面，而且新向量的長度是原兩個向量所圍成的面積大小。 a⃗×b⃗=det⁡([i^j^k^axayazbxbybz])=det

【高斯消元】CDOJ1785 曜醬的線性代數課堂（三）

++i for cnblogs mes swa eps mem else 正在高斯消元求行列式板子。 #include<cstdio> #include<cmath> #include<algorithm> #include

【高斯消元】CDOJ1783 曜醬的線性代數課堂（一）

turn abs swap size wap n) memset efi 高斯高斯消元求逆矩陣板子。 #include<cstdio> #include<cmath> #include<algorithm> #include

【高斯消元】CDOJ1784 曜醬的線性代數課堂（二）

cst %d can cstring 課堂 esp 線性 memset () 高斯消元求矩陣秩板子。 #include<cstdio> #include<cmath> #include<algorithm> #include&

機器學習中的線性代數知識（下）

關於作者作者小碩一枚，研究方向為機器學習與自然語言處理，歡迎大家關注我的個人部落格https://wangjie-users.github.io/，相互交流，一起學習成長。前言在機器學習中的線性代數知識（上）一文中，主要講解了矩陣的本質，以及對映視角下的特

線性代數三（重點）

一、最小二乘法： 1、矩陣、向量的求導法則：思路：將前面的項看作一個整體，對後面求導後再展開前面的整體。 ①行向量對元素進行求導： ②：列向量對元素進行求導： ③矩陣對元素進行求導： ④元素對行向量進行求導： ⑤元素對列、矩陣：類似上述方法。

Python OpenCV 線性濾波器簡介（七）

簡介過濾是訊號和影象處理中基本的任務。其目的是根據應用環境的不同，選擇性的提取影象中某些認為是重要的資訊。過濾可以移除影象中的噪音、提取感興趣的可視特徵、允許影象重取樣，等等。當我們觀察一張圖片時，我們觀察的是影象中有多少灰度級（或顏色）及其分佈。根據灰度

人工智慧實踐：TensorFlow筆記學習（七）—— 卷積神經網路基礎

大綱7.1 卷積神經網路7.2 lenet5程式碼講解目標掌握卷積神經網路的搭建方法7.1 卷積神經網路全連線 NN：每個神經元與前後相鄰層的每一個神經元都有連線關係，輸入是特徵，輸出為預測的結果。引數個數：（前層X後層+後層）一張解析度僅僅是28x28的黑白影象，就有

線性代數-總結（一）

線性代數的核心內容就是線性變換，前面主要從靜態和動態兩個方面進行描述，奇異值分解應該比矩陣對角化更為一般，矩陣對角化只是它的特殊情

人工智慧必備數學基礎：線性代數基礎（1）

如果需要小編其他數學基礎部落格，請移步小編的GitHub地址　　傳送門：請點選我　　如果點選有誤：https://github.com/LeBron-Jian/DeepLearningNote 　　這裡我打算再補充一下關於線性代數的基礎。　　（注意：目前自己補充到的所有知識點，均按照自己網課

人工智慧必備數學基礎：線性代數基礎（2）

如果需要小編其他數學基礎部落格，請移步小編的GitHub地址　　傳送門：請點選我　　如果點選有誤：https://github.com/LeBron-Jian/DeepLearningNote 　　這裡我打算補充一下機器學習涉及到的一些關於特徵值和特徵向量的知識點。　　（注意：目前自己補充到的所有知識點

線性代數（七）-線性方程組的解

最近忙於演算法和戰神4，導致線性代數的優先順序往後降了降，現在半個學期多過去了看了一半，立個flag學期結束錢看完，不過估計是做不到了，但是至少在寒假要開始概率論了吧。 1. 證明如下：可得求解線性方程組的步驟如下：以下為解齊次線性方程和非齊次線性方程的過程

數據結構（七）二叉樹

廣度優先 -1 XML -o 滿二叉樹 nal 如果數據中序定義特點特殊的二叉樹斜樹顧名思義，其中的結點都只有一個，又分為左斜樹和右斜樹，這時候又有疑惑了，這種數據結構不是有線性表一樣嗎，沒錯，線性表是一種特殊的樹滿二叉樹完全二叉樹

POJ 2318 TOYS （計算幾何）叉積的運用

line sync ted all names pri char ems sizeof Calculate the number of toys that land in each bin of a partitioned toy box. Mom and dad have

機器學習實戰（七）線性迴歸（Linear Regression）

目錄 0. 前言 1. 假設函式（Hypothesis） 2. 標準線性迴歸 2.1. 代價函式（Cost Function） 2.2. 梯度下降（Gradient Descent） 2.3. 特徵縮放（Feat

Unity學習（三）Unity Shader入門（基礎知識篇）+線性代數複習（未完待續）

至於為什麼剛建立了指令碼，現在就要做Shader了。。說多了都是淚 1.建立一個新的材質 Material Assert -> Create -> Material 拖到Scene中的某個物體上 2.建立一個新的Shader Assert -> Create -

Deep Learning 學習隨記（七）Convolution and Pooling --卷積和池化

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！

SVM支援向量機系列理論（七）線性支援向量機與L2正則化 Platt模型

7.1 軟間隔SVM等價於最小化L2正則的合頁損失上一篇說到， ξi ξ i \xi_i 表示偏離邊界的度量，若樣本點

線性代數基礎（矩陣、範數、正交、特徵值分解、奇異值分解、跡運算）

目錄基礎概念矩陣轉置對角矩陣線性相關範數正交特徵值分解奇異值分解跡運算行列式如果這篇文章對你有一點小小的幫助，請給個關注喔~我會非常開心的~ 基礎概念標量：一個標量就是一個單獨的數字向量：一個向量就是一列數字矩

POJ2318 （二分加叉積使用）

題目連結題目大意：給你一個矩形和一些線段，給的這些線段將矩形分割為從左到右的若干個部分（不會相交，點不會再線上，題意給出了），之後給出一些玩具的座標，求分割的若干部分每個部分的玩具數量。題解：這是一個計算幾何的水題，考一些基礎問題，我們注意，題目上給線段的順序是從左到