機器學習中的線性代數知識（下）
關於作者
作者小碩一枚，研究方向為機器學習與自然語言處理，歡迎大家關注我的個人部落格https://wangjie-users.github.io/，相互交流，一起學習成長。
前言
在機器學習中的線性代數知識（上）一文中，主要講解了矩陣的本質，以及對映視角下的特徵值與特徵向量的物理意義。本篇博文將繼續討論相關知識。
向量和矩陣的範數歸納
1、向量的範數
這裡我直接以例項講解。定義一個向量為：a=[-5, 6, 8, -10] 向量的1範數：向量的各個元素的絕對值之和，上述向量a的1範數結果就是：29； 向量的2範數：向量的每個元素的平方和再開平方根，上述a的2範數結果就是：15； 向量的負無窮範數：向量的所有元素的絕對值中最小的。上述向量a的負無窮範數結果就是：5； 向量的正無窮範數
2、矩陣的範數
定義一個矩陣A=[-1 2 -3；4 -6 6]； 矩陣的1範數：矩陣每一列上的元素絕對值先求和，再從中取最大值（列和最大）。上述矩陣A的1範數就是9； 矩陣的2範數：矩陣的最大特徵值開平方根，上述矩陣A的2範數就是：10.0623； 矩陣的無窮範數：矩陣的每一行上的元素絕對值先求和，再從中取個最大的(行和最大)，上述矩陣的結果就是：16； 矩陣的核範數：矩陣的奇異值之和(將矩陣SVD分解，文章後面會講到)，這個範數可以用低秩表示（因為最小化核範數，相當於最小化矩陣的秩——低秩），上述矩陣A最終結果就是：10.9287； 矩陣的L0範數
深入理解二範數
二範數相信大家在本科學線代的時候就已經被灌輸了“用來度量向量長度”、“用來度量向量空間中兩個點的距離”這兩個典型意義。那麼在機器學習中，二範數主要有什麼重要的應用呢？
我們經常在機器學習的loss函式中加上引數的2範數項，以減少模型對訓練集的過擬合，即提高模型的泛化能力。那麼問題來了，為什麼2範數可以提高模型的泛化能力呢？
首先假設我們model的引數為向量W=[W1, W2, …, Wn], 這個w不僅是模型的引數，更是特徵的權重！。換句話說，每個引數Wi，決定了每個特徵對決定樣本所屬類別的重要程度。
這裡我們舉一個實際例子，假設引數w的維度為5，有以下兩種情況：
- 令W1=W2=W3=W4=W5=2
- 令W1=10, W2=W3=W4=W5=0
由二範數公式：
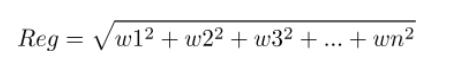1和2相比，哪個的Reg更小呢？顯然前者的值只有20，而後者的值高達100！雖然1和2的所有w的值加起來都等於10。而我們的目標是最小化loss函式，因此需要Reg也要小。由這個例子可以看出，如果我們有10張用於決定類別的票分給各個特徵，那麼給每個特徵分兩張票帶來的回報要遠大於把這10張票分給一個特徵！（不患寡而患不均），因此二範數會削弱強特徵，增強弱特徵。（有點兒劫富濟貧的意思）
那麼這種方式有什麼好處呢？
比如，假設我們在做文字的情感分類任務（判斷一段文字是正面還是負面），將每個詞作為一個特徵（出現該詞代表1，否則為0）。可想而知，有一些詞本身就帶有很強的情感極性，比如“不好”、“驚喜”等。而大部分詞是弱極性的，但是多個弱極性的詞同時出現的時候就會產生很強的情感極性。比如“總體”“來說”“還是”“可以”在文字中同時出現後基本就奠定了這篇文字的總體極性是正面的，哪怕文字中出現了“很爛”這種強負面詞。
因此在二範數的約束下，w這個隨機變數的分佈會趨向於方差u=0的高斯分佈。
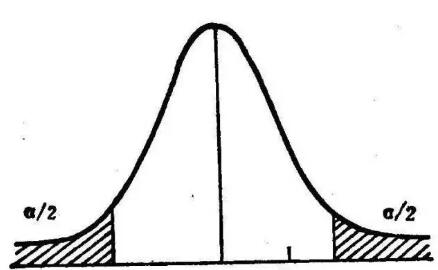當然，既然是高斯分佈，有極少的特徵值是特別大的，這些特徵就是超強特徵，比如“非常好”這個特徵一旦出現，基本整個文字的情感極性就確定了，其它的弱特徵是很難與之對抗的。所以最小化二範數會讓隨機變數的取樣點組成的向量趨向於期望=0的高斯分佈。
所以，如果沒有二範數的約束，弱特徵會被強特徵“剝削”，最終訓練完後各個特徵的權重很有可能是這樣的：
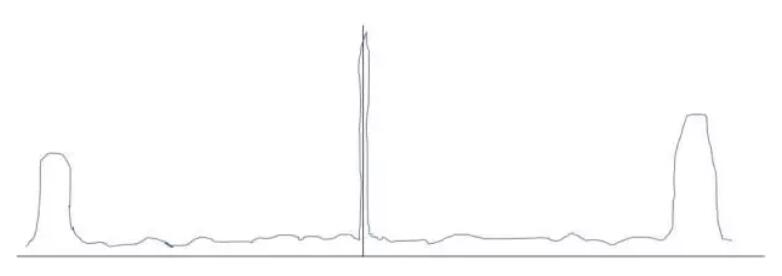這樣會帶來什麼問題呢？導致模型過分依賴強特徵。
- 首先，這樣的model拿到測試集上，一旦某個樣本沒有任何強特徵，就會導致這個樣本的分類很隨機。而如果有了二範數的約束，弱特徵們就會發揮它們的作用。
- 其次，這樣的**model抗噪聲能力非常差。**一旦測試集中的某個樣本出現了一個強特徵，就會直接導致其進行分類，而完全不考慮其它弱特徵的存在。而如果有了二範數的約束，弱特徵們就會聚沙成塔，合力打倒那個強特徵的噪聲。 那麼是不是所有的ML任務加上二範數約束就一定好呢？ 答案當然是否定的。在一些ML任務中，尤其是一些結構化資料探勘任務和特徵意義模糊的機器學習任務（比如深度學習）中，特徵分佈本來就是若干強特徵與噪聲的組合，這時加上2範數約束反而會引入噪聲，降低系統的抗噪效能，導致model的泛化能力更差。 因此，使用二範數去提高機器學習model的泛化能力大部分情況下是沒錯的，但是也不要無腦使用哦，懂得意義後學會根據任務去感性與理性的分析才是正解。這裡有一篇分析機器學習中正則化項L1和L2的直觀理解，大家可以借鑑閱讀。