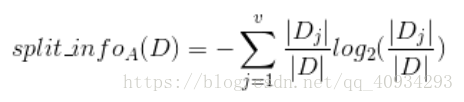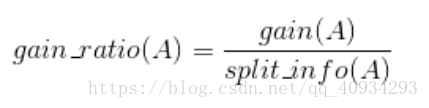決策樹概要

1. 決策樹的構造
2. ID3演算法介紹
3. 資訊熵與資訊增益
4. 決策樹的優缺點

決策樹的構造

依決策樹是託決策而建立起來的一種樹。決策樹是一個預測模型，代表的是物件屬性與物件值之間的一種對映關係。樹中每個節點表示某個物件，而每個分叉路徑則代表的某個可能的屬性值，而每個葉結點則對應從根節點到該葉節點所經歷的路徑所表示的物件的值。

選擇屬性，確定特徵屬性之間的拓撲關係。

• 關鍵：分裂屬性

1. 屬性是離散值且不要求生成二叉決策樹。此時使用屬性的每一個劃分作為一個分支。
2. 屬性是離散值且要求生成二叉決策樹。此時使用屬性劃分的一個子集進行測試，按照“屬於此子集”和“不屬於此子集”分成兩個分支。
3. 屬性是連續值。此時確定一個值作為分裂點split_point，按照>split_point和<split_point生成兩個分支。

屬性的選擇-----自頂向下，貪婪遞迴

• 分裂準則
  • 資訊增益最大化

                              

                              

1. 計算各屬性的資訊增益
2. 選擇具有最大資訊增益的屬性作為第一個分裂點
3. 繼續對中間資料集重複1.

ID3演算法介紹

ID3演算法的核心思想就是以資訊增益來度量屬性的選擇，選擇分裂後資訊增益最大的屬性進行分裂。因為資訊增益越大，區分樣本的能力就越強，越具有代表性，所以該演算法採用自頂向下的貪婪搜尋遍歷可能的的決策空間。

ID3的缺陷與改進：

• 偏向性：傾向於選擇多值屬性。
• 解決方案：資訊增益率（C4.5）
  • 引入分裂資訊：

                  

•   增益

          

資訊熵與資訊增益

資訊的定義：如果待分類的事務可能劃分在多個分類之中，則符號xi的資訊定義為：l(xi)=-log2p(xi)；其中p(xi)是選擇該分類的概率。

資訊熵則是定義為資訊的期望值。

假如一個隨機變數的取值為，每一種取到的概率分別是，那麼

   的熵定義為

             

意思是一個變數的變化情況可能越多，那麼它攜帶的資訊量就越大。

對於分類系統來說，類別是變數，它的取值是，而每一個類別出現的概率分別是

             

   而這裡的就是類別的總數，此時分類系統的熵就可以表示為

           

資訊增益是針對一個一個特徵而言的，就是看一個特徵，系統有它和沒有它時的資訊量各是多少，兩者的差值就是這個特徵給系統帶來的資訊量，即資訊增益。

 資訊增益的計算公式如下

   

其中為全部樣本集合，是屬性所有取值的集合，是的其中一個屬性值，是中屬性的

   值為的樣例集合，為中所含樣例數。

決策樹的優缺點

優點：可解釋性強；無需資料預處理；能同時處理數值型和常規資料型別；對缺失值不敏感；可以處理不相關特徵資料。

缺點：可能會產生過度匹配問題

適用資料型別：數值型和標稱型

解決產生過度匹配問題：通過裁剪決策樹，合併相鄰的無法產生大量資訊增益的葉節點