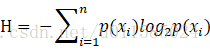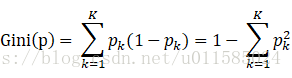本文為作者學習K近鄰演算法後的整理筆記，僅供學習使用！

決策樹

1、概述 

  決策樹（Decision Tree）實在已知各種情況發生概率的基礎上，通過構成決策樹來求取淨現值的期望值大於等於0的概率，評價專案風險，判斷其可行性的決策分析方法，是直觀運用概率分析的一種圖解法。

2、基本原理

（1）工作原理：

     a、獲取原始資料集

     b、基於最好的屬性值劃分資料集

     c、資料將向下傳遞到樹分支的下一個節點，再這個節點上，可以再次對資料進行劃分

（2）遞迴結束的條件：

     a、程式遍歷完所有劃分資料集的屬性

     b、每個分支下的所有實力都具有相同的分類

3、優缺點

（1）優點

    計算複雜度不高，輸出結果易於理解，對中間值的缺失不敏感，可以處理不相關特徵資料

（2）缺點

    可能會產生過度匹配問題（過擬合）

  適用資料型別：數值型和標稱型

4、一般流程

（1）收集資料：可以使用任何方法

（2）準備資料：樹構造演算法只適用於標稱型資料，因此數值型資料必須離散化（資料預處理）

（3）分析資料：可以使用任何方法，構造樹完成之後，檢查圖形是否符合預期

（4）訓練演算法：構造樹的資料結構

（5）測試演算法：使用經驗樹計算錯誤率

（6）使用演算法：此步驟可以使用於任何監督學習演算法

5、構建決策樹：ID3是演算法

（1）簡介

    a、對於例項，計算各個例項的資訊增益

    b、將資訊增益最大的屬性作為根節點，根節點的各個取值作為子集進行分類

    c、對於子集下， 若只含有正例或反例，直接得到判決；否則遞迴呼叫演算法，再次尋找子節點

（2）公式以及名詞解釋

    a、公式

    b、名詞解釋

      夏農熵：表示資料集的不確定性

      條件熵：在某個條件下，資料集的不確定性

      資訊增益：香濃熵 - 條件熵，在某一條件下，資訊不確定性減少的程度

（3）缺點：

    ID3採用的資訊增益度量存在一個缺點：它一般會選擇屬性值較多的Feature。資訊增益反映的是給定一個條件以後不確定減少的程度，必然是分得越細的資料集的確定性越高，也就是條件熵越小，資訊增益越大。

    當資料集中存在自增列（ID）時，採用ID3演算法會將ID列作為根節點。

（4）程式碼示例

    a、建立資料集

# 建立資料集
def create_dataset():
    dataset = [[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,0,'no']]
    label = ['no surfacing', 'flippers']
    return dataset, label

    b、計算香濃熵

# 獲取夏農熵
def calc_shannon_ent(dataset):
    label_count = len(dataset)
    entries_count = {}
    
    for entry in dataset:
        current_label = entry[-1]
        if current_label not in entries_count:
            entries_count[current_label] = 0
        entries_count[current_label] += 1
    
    shannon_ent = 0.0
    for key in entries_count:
        probability = float(entries_count[key]) / label_count # 求概率
        shannon_ent -= probability * log(probability, 2)
    return shannon_ent

    c、選擇最優的特徵進行拆分資料集

# 拆分資料集
def split_dataset(dataset, axis, value):
    new_dataset = []
    for data in dataset:
        if data[axis] == value:
            reduced_data = data[:axis]
            reduced_data.extend(data[axis+1 : ])
            new_dataset.append(reduced_data)
    return new_dataset

# 選擇最優的特徵進行拆分資料集
def choose_best_feature_to_split(dataset):
    num_features = len(dataset[0]) - 1  # 特徵數
    base_entropy = calc_shannon_ent(dataset) # 計算夏農熵
    best_info_gain = 0.0
    best_feature = -1 # 最優特徵
    for i in range(num_features):
        feature_list = [example[i] for example in dataset]
        unique_vals = set(feature_list)
        new_entropy = 0.0
        for value in unique_vals:
            sub_dataset = split_dataset(dataset, i, value)
            prob = len(sub_dataset) / float(len(dataset)) # 概率
            new_entropy += prob * calc_shannon_ent(sub_dataset) # 拆分後夏農熵
        info_gain = base_entropy - new_entropy
        if(info_gain > best_info_gain):
            best_info_gain = info_gain
            best_feature = i
    return best_feature

    d、構建決策樹

def majority_cnt(class_list):
    class_count = {}
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
            class_count[vote] += 1
        sorted_class_count = sorted( class_count.iteritem(), key=operator.itemgetter(1), reversed = True)
        return sorted_class_count[0][0]
    
def create_tree(dataset, labels):
    class_list = [example[-1] for example in dataset]
    if(class_list.count(class_list[0]) == len(class_list)):
        return class_list[0]
    if len(dataset[0]) == 1:
        return majority_cnt(class_list)
    best_feature = choose_best_feature_to_split(dataset)
    best_feature_label = labels[best_feature]
    my_tree = {best_feature_label:{}}
    del(labels[best_feature])
    feature_values = [example[best_feature] for example in dataset]
    unique_values = set(feature_values)
    for value in unique_values:
        sub_labels = labels[:]
        my_tree[best_feature_label][value] = create_tree(split_dataset(dataset, best_feature, value), sub_labels)
    return my_tree

    e、使用構建好的決策樹

# 使用
def my_classify(input_tree, featLabels, textvec):
    first_key = list(input_tree.keys())[0]
    second_dict = input_tree[first_key]
    feat_index = featLabels.index(first_key)
    for key in second_dict.keys():
        if textvec[feat_index] == key:
            if type(second_dict[key]).__name__ == "dict":
                classLabel = my_classify(second_dict[key], featLabels, textvec)
            else:
                classLabel = second_dict[key]
    return classLabel

    f、儲存

# 儲存
def store_tree(input_tree, file_name):
    import pickle
    fw = open(file_name, 'wb')
    pickle.dump(input_tree,fw)
    fw.close()

def grab_tree(file_name):
    import pickle
    fr = open(file_name, 'rb')
    return pickle.load(fr)

    g、呼叫

my_data, labels = create_dataset()
my_tree = create_tree(my_data, labels.copy())
store_tree(my_tree, "DecisionTree.txt")
my_load_tree = grab_tree("DecisionTree.txt")
predict_label1 = my_classify(my_load_tree, labels, [1,0])
predict_label2 = my_classify(my_load_tree, labels, [1,1])

print(predict_label1, predict_label2)

6、構建決策樹：C4.5

（1）  C4.5是對ID3演算法的改進，相對於ID3演算法主要有以下幾個方面的改進：

    （a）用資訊增益比來選擇屬性

    （b）在決策樹的構造過程中

    （c）對非離散資料也能處理

    （d）能夠對不完整資料進行處理

（2）公式

7、構建決策樹：CART

（1）CART演算法是通過GINI係數選擇最優特徵，同時決定該特徵的最優二值切分點

（2）公式

8、剪枝策略

（1）預剪枝

    邊建立決策樹邊進行剪枝的操作（更實用）。通過限制決策樹深度、葉子節點個數、葉子節點樣本樹，資訊增益量等進行預剪枝操作。

（2）後剪枝

    當建立完決策樹之後來進行剪枝操作。通過一定的衡量標準（葉子節點越多，損失越大）：