@Little C Loves 3 [email protected]

@題目描述 - [email protected]

time limit per test: 1 second memory limit per test: 256 megabytes

Little C loves number «3» very much. He loves all things about it. Now he is playing a game on a chessboard of size n×m. The cell in the x-th row and in the y-th column is called (x,y). Initially, The chessboard is empty. Each time, he places two chessmen on two different empty cells, the Manhattan distance between which is exactly 3. The Manhattan distance between two cells (xi,yi) and (xj,yj) is defined as |xi−xj|+|yi−yj|.

He want to place as many chessmen as possible on the chessboard. Please help him find the maximum number of chessmen he can place.

Input A single line contains two integers n and m (1≤n,m≤10^9) — the number of rows and the number of columns of the chessboard.

Output Print one integer — the maximum number of chessmen Little C can place.

Examples

input 2 2 output 0

input 3 3 output 8

Note In the first example, the Manhattan distance between any two cells is smaller than 3, so the answer is 0. In the second example, a possible solution is (1,1)(3,2), (1,2)(3,3), (2,1)(1,3), (3,1)(2,3).

@中文題意@

n*m的矩陣，當兩個點(x1, y1)與(x2, y2)曼哈頓距離為3時可以將兩個點匹配。每個點只能夠與一個點匹配。求最多能可以匹配多少個點。 n,m <= 10^9

@分析@

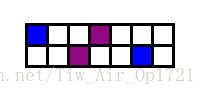
【這種題也只能夠手算小資料來找規律……】 首先弄清楚一個上界：對於任意的$n*m$矩陣，如果n與m都為奇數，則答案最大為nm-1；否則答案最大為nm。 不妨假設n <= m。 當 n = 1 的時候，我們只能橫著進行匹配。我們手算幾組資料，可以用如下圖的方法可以把$1*6$所有點都匹配。 再手算幾組，我們發現這樣一個規律：對於任意一個$1*m$，如果m%6<=3，則能匹配的點數為m-m%6；否則能匹配的點數為m-6+m%6。 【具體的證明應該可以用歸納法證明，請容許我偷一下懶qwq】

當 n = 2 的時候。$2*2$顯然無解，$2*3$的矩陣中間那一列的元素沒有任何元素能跟它們匹配，所以最大匹配點數也只能為4。$2*4$，$2*5$可以採用下列所示的方法全部匹配完。 $2*6$矩陣可以把它拆成兩個$1*6$的矩陣，每個矩陣內部可以全部匹配完。 然後！學長們就是被$2*7$的矩陣卡掉了。實際上$2*7$不能構造出全部匹配的情況的。如圖：兩個藍色塊只能與兩個紫色塊匹配，所以紫色塊只能與藍色塊匹配。同理，兩個紅色塊只能與兩個棕色塊匹配，所以棕色塊只能與紅色塊匹配。然後有一個塊既要和藍色塊匹配又要和棕色塊匹配，所以不可能~ 所以$2*7$最多隻能配對12個點。 然後，最關鍵的來了。對於一個$2*m$（m>=7），如果m為偶數，我們可以把m拆成若干個4與6的和，即將原矩陣拆成若干個$2*4$矩陣與$2*6$矩陣。對於這些矩陣我們可以把所有點匹配完，所以我們自然也就可以匹配完$2*m$的所有點；反之，如果m為奇數，我們可以先將$2*m$分成$2*5$與$2*(m-5)$兩個部分，$2*5$可以匹配完。又因m-5是個偶數，所以奇數也可以得到相似的結論。 即：$2*m（m&gt;= 7）$的矩陣，答案總可以達到上界$2*m$

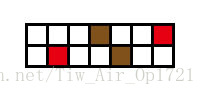
下一步，當n = 3的時候。 $3*3$，$3*4$，$3*5$的構造如下： $3*6$就可以分成3個$1*6$拼出，就不畫圖了。 於是，對於一個$3*m$的矩陣，一樣地，如果m是偶數，就將m拆成若干個4與6的和；否則就拆成(m-3)與3。所以，$3*m（m&gt;=3）$的答案也總是可以達到上界

對於n = 4，我們已知$4*2$，$4*3$可以構造出來。$4*4$可以拆成兩個$4*2$。類似的推理，$4*m（m&gt;=4）$的答案總可以達到上界。

對於n = 5，我們已知$5*2$，$5*3$，$5*4$可以構造出來。因此$5*m（m&gt;=5）$的答案總可以達到上界。

對於n = 6，我們已知$6*1$可以構造出來。因此$6*m（m&gt;=6）$的答案總可以達到上界。

然後，對於n>6。如果n為偶數，可以把n拆成若干個4與6的和；否則如果m為偶數，可以把n拆成若干個4與6的和；否則，可以把n拆成(n-3)與3，然後重複上面的推理。因此$n*m（n&gt;6, m&gt;n）$的答案總可以達到上界。

至此，本題就Over了。

@程式碼@

圖片可能看起來有些太鮮豔了……但是我也不知道什麼更好的方法可以表達“將兩個點匹配起來”qwq…… 如果眼睛瞎了，請不要打我qwq 一樣地，如果有任何的疑問或者bug，可以留言在下面告訴我，我會盡力解答你們的疑惑的qwq！

#include<cstdio>
#include<algorithm>
using namespace std;
int main() {
	int n, m;
	scanf("%d%d", &n, &m);
	if( n > m ) swap(n, m);
	if( n == 1 ) {
		if( m % 6 == 0 )
			printf("%d\n", m);
		else if( m % 6 <= 3 )
			printf("%d\n", m-(m%6));
		else printf("%d\n", m-(6-m%6));
	}
	else if( n == 2 && m == 2 )
		printf("%d\n", 0);
	else if( n == 2 && m == 3 )
		printf("%d\n", 4);
	else if( n == 2 && m == 7 )
		printf("%d\n", 12);
	else {
		if( n % 2 == 1 && m % 2 == 1 )
			printf("%I64d\n", 1LL*n*m-1);
		else printf("%I64d\n", 1LL*n*m);
	}
}

@[email protected]

就是這樣，新的一天裡，也請多多關照哦(ノω<。)ノ))☆.。