字串匹配的一般演算法（BF）

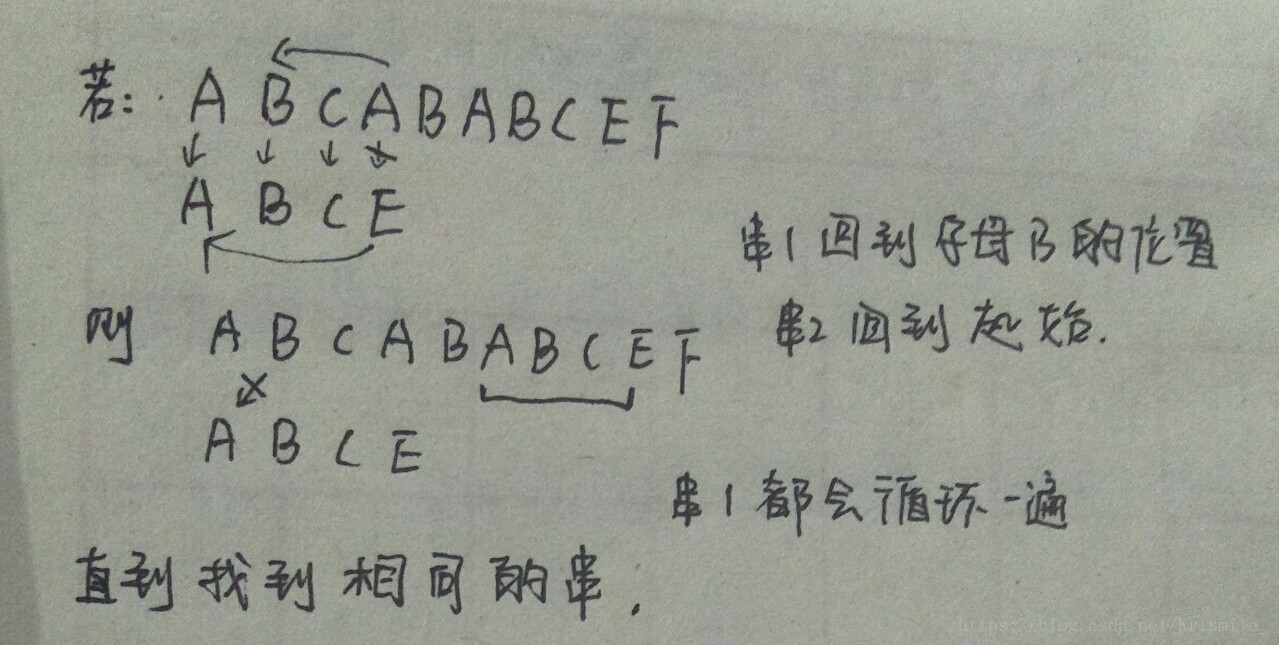
  以 ABSABABCEF 與 ABCE 為例，求串2與串1匹配的第一個位置的下標（這裡即輸出 5），一般的，我們可以從串1的起始位置開始與串2比較，若相同則兩串都向後移，否則，串1回到第二個位置，串2回到起始位置重新比較。

程式碼：（以hdu1771為例）

本題用此方法會超時

#include<stdio.h>
int a[10001],b[10001];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int m,n;
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        for(int j=0;j<m;j++)
            scanf("%d",&b[j]);
        int k=0,s=0;
        while(k<n&&s<m)
        {
            if(a[k]==b[s]){  //若相同，都向前進
                k++;s++;
            }
            else{
                k=k-s+1;    //若不相同，串1回到k-s+1的位置，串2回到起始位置
                s=0;
            }
            if(s==m){
                printf("%d\n",k-s+1);
                break;
            }
        }
        if(s!=m)
            printf("-1\n");
    }
    return 0;
}
 

字串匹配KMP演算法

從上面一般演算法中我們可以看到兩字串需要不斷地回溯，這會導致複雜度增加，複雜度為O(M*N)，再M，N過大的情況下會超時，因此有了KMP演算法。

圖1 

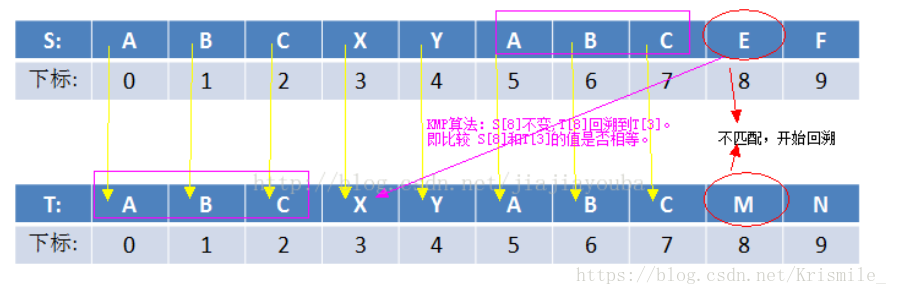
 從上圖中可以看出我們不必讓串1回溯，串2也不必每次都回溯到起始位置，那麼我們怎麼判斷讓串2回溯到什麼位置你呢？這裡引入字串字首和字尾的最長匹配長度，用pmt陣列儲存，為了方便我們再使用Next陣列。

圖2.

 如圖一所示，比較至8的位置開始不相同，那麼8之前的7個元素都是相同的，那麼由前圖2可知長度為7的字串的字首和字尾的最長匹配長度為3，所以我們可以知道串2只需要回退到pmt[7-1]的位置，即Next[7]的位置，所以我們用此方法來解決這道題。

AC程式碼（都以hdu1711為例）

#include<stdio.h>
int a[1000001],b[10001],Next[100001];    //求Next陣列
void getNext(int m)
{
    int i=0,j=-1;
    Next[0]=-1;
    while(i<m){
        if(j==-1||b[i]==b[j]){
            i++;j++;
            Next[i]=j;
        }
        else
            j=Next[j];
    }
    return ;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int m,n;
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        for(int j=0;j<m;j++)
            scanf("%d",&b[j]);
        int k=0,s=0;
        getNext(m);
        while(k<n&&s<m)
        {
            if(a[k]==b[s]||s==-1){
                k++;s++;
            }
            else{
                s=Next[s];
            }
            if(s==m){
                printf("%d\n",k-s+1);
                break;
            }
        }
        if(s!=m)
            printf("-1\n");
    }
    return 0;
}