KMP演算法包括兩個子程式。其中KMP-MATCHER指字串匹配子程式，COMPUTE-PREFIX則為部分匹配表NEXT[]生成程式。《演算法導論》一書中有一句話，我認為說的非常透徹：“這兩個程式有很多相似之處，因為它們都是一個字串對模式P的匹配：KMP-MATCHER是文字T針對模式P的匹配，COMPUTE-PREFIX是模式P針對自己的匹配。”

建議在閱讀本文之前，先花上半小時閱讀阮一峰老師的《字串匹配的KMP演算法》一文，這篇文章簡短精悍，快速讓你明白什麼KMP演算法、什麼是部分匹配表（也就是常見的NEXT[]陣列）。

閱讀完畢阮一峰老師的文章，你應該可以根據前後綴的概念，手動求出部分匹配表NEXT[]

。不妨試試下面這個例子（《該例子摘自《演算法導論》》）——字串 $P=ababaca$

P=ababaca 。其中，q表示索引號，string表示字串，next[7]則為字串對應的部分匹配表。

你的結果與上述表格中的一樣嗎？OK，部分匹配表NEXT[]已經有了。那麼，如何利用部分匹配表在必要時快速滑動呢？

舉個例子，假設 $T=(\mathrm{.}$

. . b a c b a b a b a a b c a b . . . ) T=(...bacbababaabcab...) 為一個很長的字串（以下為截斷部分）， $P=(ababaca)$為一個較短的被搜尋的字串。

下圖中在P[5]處出現了不匹配情況。此時，我們希望P字串快速向右滑動…要滑動到什麼位置呢？——也就是滑動到，（此刻） $P=(aba'ba)$的字首與 $T=(...bacbab'aba)$的字尾匹配處 。

問題1： 為什麼可以這麼滑動？我們可以將字串P視為這樣的結構“[([字首，中間，字尾])，剩餘部分]”，其中恆有 “[字首]==[字尾]”。（見下圖）

那麼，當在後綴 之後 位置出現不匹配時（暗示著，此時T、P兩字串的前面部分全匹配——都為([字首，中間，字尾])），立即將 $P$ 串的字首滑動到與字尾重合的位置，如 $P'$ 所示，繼續開始後續的匹配。

問題2： 問題1的基礎是，恆有 “[字首]==[字尾]”？這個如何保證？也就是怎麼選取這個分割點？正好，部分匹配表NEXT[]就是用來回答這個問題的。

我們就針對上圖出現不匹配時刻，來看看此時的模式 $P=(ababaca)$ 是如何被分割為“字首”、“字尾”。下面這張表格是模式P針對自己的匹配，當前正在進行上文中NEXT[4]計算階段。（可見，字尾部分為P[2] ~ P[4]，字首部分是P[0] ~ P[2]。）

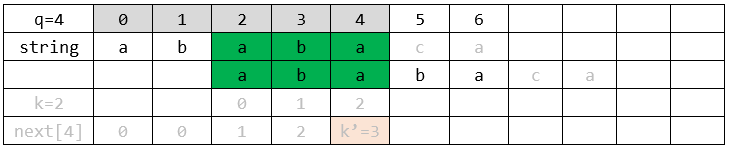
此時，NEXT[4]記錄的是字首的匹配長度（ $k'=3$）。好了，上文說在P[4]後發生了失配（根據上文的“[([字首，中間，字尾])，剩餘部分]”，此時後綴最後一個字元為P[4]），我們需要將其對應的字首（P[0] ~ P[2]）滑動過來與字尾對齊。根據NEXT[]計算對齊的公式：
$s'=s+(q-next[q])$所以， $s'=s+(4-next[4])=s+2$，也就是將字串P迅速向右滑動2個格子。

本文程式碼與《演算法導論》一書保持基本一致，但是鑑於書上下標是從1開始的，不太符合C++程式的風格。這裡參考了c_cloud的《【經典演算法】——KMP，深入講解next陣列的求解》一文，將下標改為從0開始。以下為KMP-MATCHER子程式（簡單說明下kmp_matcher子程式的工作原理。以下主要分為三種情況討論）：

int kmp_matcher(const string& t, const string& p) {
	int lt = t.size(), lp = p.size();
	vector<int> next = compute_prefix(p);
	for (int i = 0, q = 0; i < lt; ++i) {
		while (q > 0 && p[q] != t[i]) {
			q = next[q-1];
		}
		if (p[q] == t[i]) {
			++q;
		}
		if (q == lp) {
			return i - lp + 1;
		}
	}
	return -1;
}

其一，如果字串T、P當前位情況為匹配，那就直接看下一位是否匹配…，如果匹配長度達到了字串P的總長度，那麼匹配成功，返回（結束）。

其二，如果字串T、P當前位情況為不匹配“[([字首，中間，字尾])，剩餘部分]”，那麼就要根據此刻的位置，從NEXT[]中取出對應字首的位置，然後根據上文的公式，將字首滑動過來與字尾對齊，繼續後續匹配工作…。（注意，此過程是遞迴進行的，遞迴出口為“其一”或“其三”所描述的情況有發生）

其三，（可以看做其二的一個特例）如果字串T與字串P的第1位（也就是P[0]）就失配了。此時就不要進行“其二”的步驟了，而應該將字串T的下一位與P[0]進行匹配。

以下為部分匹配表生成子程式COMPUTE-PREFIX（這裡我不再說明這部分程式了，我在文後附上一個例子）。再次引用《演算法導論》一書中的一句話，我認為說的非常透徹：“這兩個程式有很多相似之處，因為它們都是一個字串對模式P的匹配：KMP-MATCHER是文字T針對模式P的匹配，COMPUTE-PREFIX是模式P針對自己的匹配。”

//部分匹配表NEXT[]
std::vector<int> compute_prefix(const string& p) {
	int lp = p.size(), k = 0;
	std::vector<int> next(lp, 0);//next[0] = 0
	for (int q = 1; q < lp; ++q) {
		while (k > 0 && p[k] != p[q]) {
			k = next[k-1];
		}
		if (p[k] == p[q]) {
			++k;
		}
		next[q] = k;
	}
	return next;
}

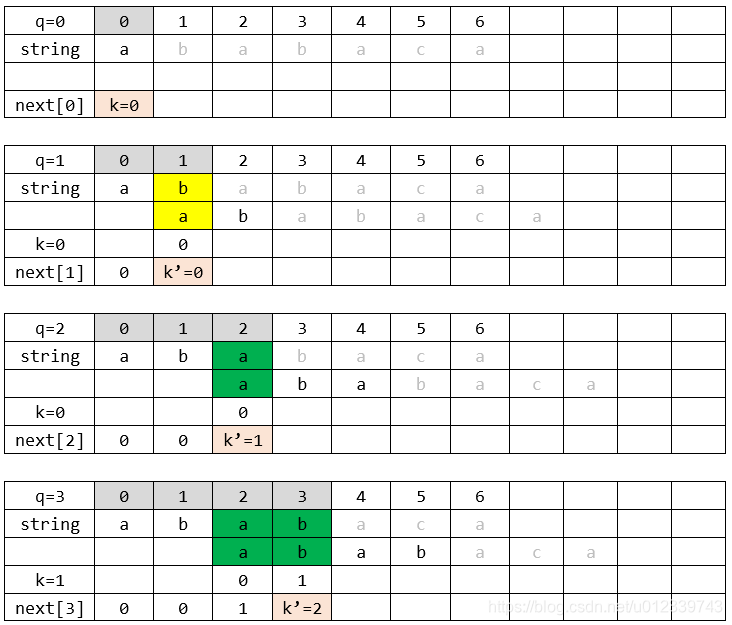
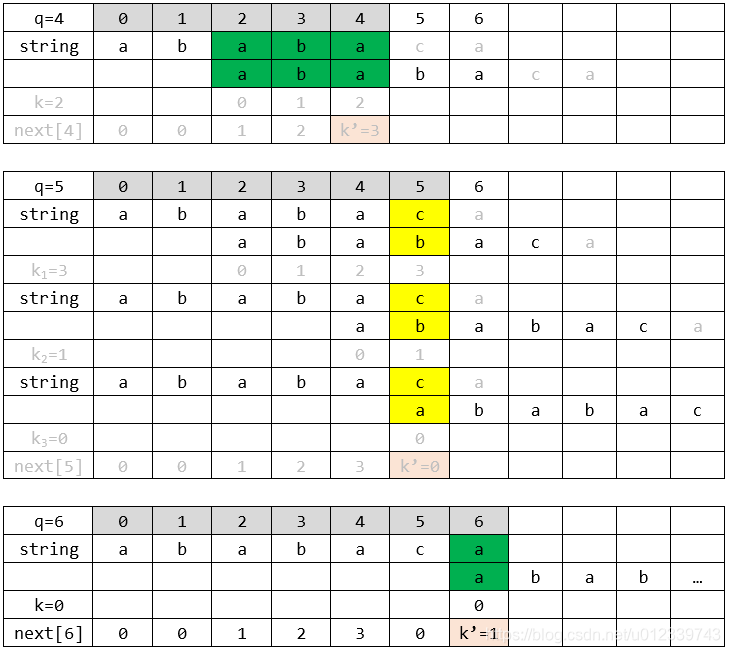
附上的例子：對字串 $P=(ababaca)$，COMPUTE-PREFIX子程式運算的視覺化過程，可能對你有用。

©為徑
2018-12-27 北京 海淀

References:
[1] Thomas H.Cormen 《演算法導論》 588頁~594頁
[2] 阮一峰的《字串匹配的KMP演算法》，2018-12-27
[3] c_cloud的《【經典演算法】——KMP，深入講解next陣列的求解》，2018-12-27