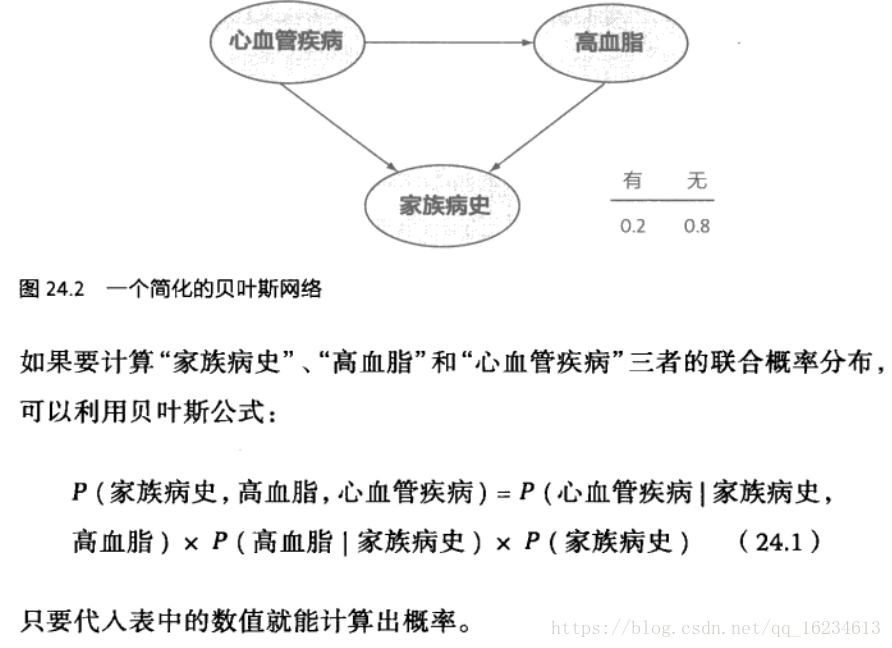
數學之美:馬爾科夫鏈的擴充套件-貝葉斯網路 詞分類
前面介紹的馬爾科夫鏈是一種狀態序列,但在實際中,各個事物之間不僅使用鏈序列起來的,而是互相交叉,錯綜複雜。因此通過各個事物之間的聯絡,可以將馬爾科夫鏈推廣至圖論中。
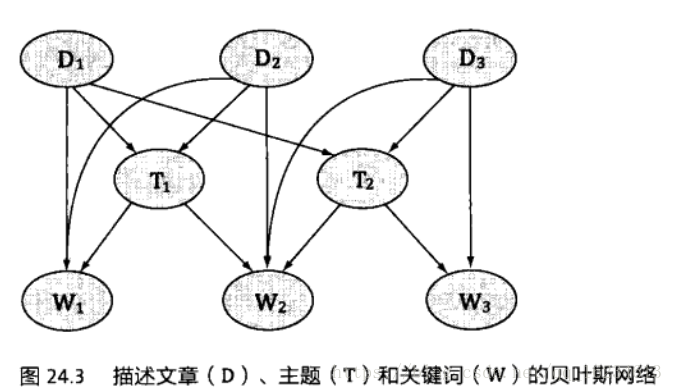
沒想到貝葉斯網路還可以用於詞分類。在前面我們介紹到通過使用SVD可以對文字進行分類,如果把文字和關鍵詞的關聯矩陣轉90度。進行奇異值分解,或者對每個詞建立文字向量,再聚類。那麼我們得到的就是關於詞的分類,稱之為概念。顯然一個概念可以包含多個詞,一個詞也可以屬於多個概念。現在使用貝葉斯網路對這些文字、概念和關鍵詞建立網路:
圖中,文章和關鍵詞有直接關聯,同時與主題也有直接關聯,通過主題還有間接關聯。通過這個圖可以找到每個關鍵詞與概念之間關係,詞與詞之間的相關性。google的rephil網路就是建立文章、詞和概念之間的關係,將上百萬詞聚類成若干概念類。在廣告和搜尋中應用廣泛。
使用貝葉斯網路首先就要確定其結構,對簡單網路,專家可以直接給出;對於複雜的網路就需要機器學習了。
優化的貝葉斯網路要保證其產生的序列從頭到尾可能性最大,如果使用概率度量,那就是後驗概率最大。但是產生一個序列可以有多條路徑,從理論上講,需要完備搜尋,考慮每一條路徑,得到全域性最優。但這樣計算的複雜度是NP-Hard。因此一般採用貪心演算法,每次沿著箭頭走有限步,但這樣容易陷入區域性最優。一個防止區域性最優的演算法就是蒙特卡洛方法,用許多隨機數測試,看看是否顯然區域性最優。這個方法的計算量較大,最近的新方法是計算節點兩兩之間的互資訊,只保留互資訊較大的直接連線,簡化網路後再完備搜尋。
在確定網路結構後就需要確定節點間的權重,假設使用條件概率來度量權重,那就需要訓練資料,使得網路在這些觀察到的資料上概率最大,即EM過程。
需指明結構的訓練和引數的訓練是交替進行的,先優化引數,再優化結構,然後再次優化引數,直到模型收斂,或誤差足夠小。