數學之美_馬爾科夫模型01
1. 概率:是一種分析問題的範型(也可以說一種分析問題的模板)
2. 馬爾科夫:是一個人名。
2.1 生平:俄國數學家,出生於梁贊州。位置靠近歐洲。
模樣就是張這個樣

父親是一位中級官員,後來居家遷往聖彼得堡,1794年馬爾科夫進入聖彼得堡大學,是從切比雪夫。畢業後留校任教。
詳細生平:
https://baike.baidu.com/item/%E5%AE%89%E5%BE%B7%E9%9B%B7%C2%B7%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB/10445098
3. 馬爾科夫最偉大的成就就是馬爾科夫鏈,路徑。關鍵字:馬爾科夫鏈,馬爾科夫矩陣,隱馬爾科夫。馬爾科夫屬於概率論這個範疇中的一種模型。
隱馬爾可夫並不是馬爾科夫發明的。現代概率論的一位大牛!
4. 馬爾科夫預測:
公理:一切用於實際應用的屬性模型都需要實際情況的檢驗。
推論1:實踐是檢驗真理的唯一標準。
推論2:一切預測模型僅僅只是預測。
性質:
1、有效性:預測給出了未來發生實踐的可能值(不是可能值)。
2、差異性:預測與實際值一定有差別(注意:是一定!)。
3、可控性:優良的模型給出預測值與實際值相差不可能太大(誤差太大就不叫預測了)。
第一個問題:資訊耗散
*一則訊息在a1、a2、a3,... ,an...這麼多人中一次傳遞,每次傳遞該訊息會出現訊息的失真,失真的概率為p,那麼第n個人獲得訊息的可靠程度如何?
舉例:擊鼓傳花、訊息傳遞遊戲等等,在現實過程中非常多的例子。
第二個問題:愚蠢的顧客
*某同類物品A、B、C的宣傳力度不同,愚蠢的顧客在廣告宣傳的效應下,第一次嘗試選擇購買A、B、C的概率為0.2,0.4,0.4。
*經銷商統計,顧客的購買傾向為下標,嘗試求某顧客第四次來購買格物品的概率。
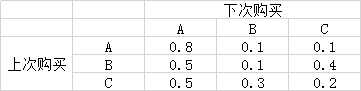
起源:
*20世紀初,馬爾科夫(Markov)研究自然界有一類事物變化過程僅與事物的近期狀態有關,與事物過去的狀態無關(很像LSTM模型)。
*這樣的性質稱為馬爾科夫性,或無記憶性,或者無後效性(像金魚一樣,吃了東西忘了還吃過,繼續吃)。
*例如:一個商店的累計賺了多少錢,如果現在時刻的盈利已知,則未來某一時刻的盈利數目與現在時刻以前的任一時刻盈利額無關。
隨機遊走、布朗運動:
*一個質點在零時刻位於原點,每間隔單位時間右移或者左移一個單位長度,右移動的概率為p,左移動的概率為1-p,質點在第n個時刻的位置為X(n),n=0.1,...這樣的過程叫馬爾科夫過程(馬爾科夫構成可以理解成:現實中無腦的遊走過程)。
*布朗運動就是一個馬爾科夫過程。
*這裡只討論離散的馬爾科夫過程(大學有一門課程叫隨機過程,有興趣的話可以看一下這個《隨機過程》)。
名詞鋪墊:
* 隨機過程的本質就是對一系列隨機變數的整體描述。
*定義(非純數學的):T是一個實數集合,如果對任意的t∈T,αt是一個隨機變數,那麼我們把全部的αt擱一塊兒{α,t∈T},就稱為隨機過程,t可以簡單理解為時間,αt的全體取值即可成為狀態空間。
*定義:如果我們知道這麼一個隨機序列,狀態空間E是可列的。如果i,j∈E,k = 1,... n-1,如果有這麼一個式子,

就是一個馬爾科夫鏈,具備馬爾科夫性。也就是說當前時刻的狀態只和前一個時刻的狀態有關。
時齊性與轉移概率

時齊性:就是前面說的只和前一個時刻有關。
轉移概率:就是轉移概率矩陣Pij(m)表示i狀態轉移到j狀態,轉移了m次
轉移概率矩陣:

*馬克科夫預測的核心在於轉移概率矩陣的確立。
*去誒定這些概率的的方法,可以是統計,可以理論分析,甚至是猜測的。
柯爾莫哥洛夫-郄普曼方程(K-C方程)
馬爾科夫預測模型:

舉一個例子:
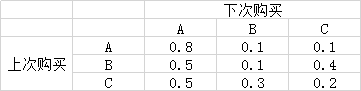
還是以上面一個例子:
1. 初始狀態為:0.2 0.4 0.4
2.轉移概率矩陣為上面那個東西。
因此用matlab賦值
>> s = [0.2 0.4 0.4]
s =
0.2000 0.4000 0.4000
>> p = [0.8 0.1 0.1;0.5 0.1 0.4;0.5 0.3 0.2]
p =
0.8000 0.1000 0.1000
0.5000 0.1000 0.4000
0.5000 0.3000 0.2000
>>
如果是第一次來購買這個物品的概率為s*p^1,如果第四次就是s*p^4
>> s * p^4
ans =
0.7101 0.1327 0.1572
另外我們發現經過多次傳遞之後,這個值會不變了
>> s * p^400
ans =
0.7143 0.1310 0.1548
>> s * p^401
ans =
0.7143 0.1310 0.1548
>> s * p^402
ans =
0.7143 0.1310 0.1548
>> s * p^399
ans =
0.7143 0.1310 0.1548
