1、陣列和連結串列的區別：

陣列的特點：

1. 陣列在記憶體中是連續的區域
2. 陣列的大小需要提前申請，即需要提前確定大小。不利於擴充套件，可能導致用不完而浪費
3. 陣列資料的插入刪除，需要移動後面的資料，效率低
4. 陣列讀取是隨機的，可以通過下表隨機讀取，效率高
5. 儲存密度為1

連結串列的特點：

1. 連結串列在記憶體中不要求空間，可以是任何地方，可以斷斷續續的。
2. 增加和刪除資料很容易，只需要改變新增位置的前後兩個資料單位的指標就行
3. 查詢資料是順序的，效率低
4. 連結串列的大小可以不指定，方便擴充套件
5. 儲存密度<1(因為結點中有指標域)

陣列的優點：隨機訪問，查詢效率高

缺點：插入和刪除效率低、可能造成記憶體浪費、記憶體必須是連續、陣列大小要提前固定，不能動態擴充套件

連結串列的優點：插入刪除速度快、記憶體利用率高，大小易擴充套件

缺點：查詢效率低

2、簡述快速排序的過程：

1. 選擇一個基準元素，通常選擇第一個或者最後一個；
2. 通過一趟將待排序的記錄分成獨立的兩部分，其中一部分比基準值小，一部分比基準值大。基準值已經排好在正確位置；
3. 然後分別對兩部分為排序記錄用同樣的方法進行排序，直到整個序列有序。

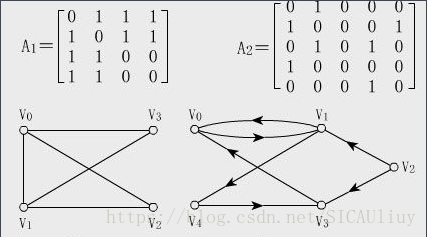
3、鄰接矩陣與鄰接表的：

鄰接矩陣：用一個二維陣列存放頂點間關係（邊或弧），無向圖為兩點間是否有連線可達，有向圖是兩點間是否有到達方向的連線。

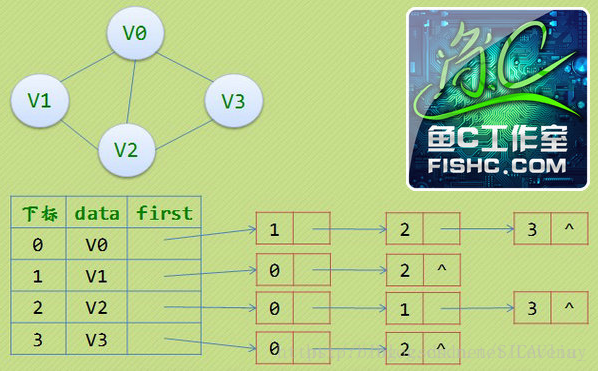
鄰接表：圖中頂點用一個一維陣列儲存，圖中每個頂點vi的所有鄰接點構成單鏈表

對比：

1. 在鄰接矩陣中，無向圖的鄰接矩陣是對稱的。矩陣中的第i行或第i列有效元素個數之和就是頂點的度；

在有向圖中第i行有效元素個數和是頂點的出度，第i列有效元素個數之和是頂點的入度。

1. 在鄰接表的表示中，無向圖的同一條邊在鄰接表中儲存的兩次。如果想要知道頂點的度，只需要求出所對應連結串列的結點個數即可。

有向圖中每條邊在鄰接表中只出現一次，求頂點的出度只需要遍歷所對應連結串列即可。求入度則需要遍歷其他頂點的連結串列。

（3）鄰接矩陣與鄰接表優缺點：

鄰接矩陣的優點是可以快速判斷兩個頂點之間是否存在邊，可以快速新增邊或者刪除邊。而其缺點是如果頂點之間的邊比較少，會比較浪費空間。因為是一個 n∗n 的矩陣。

而鄰接表的優點是節省空間，只儲存實際存在的邊。其缺點是關注頂點的度時，就可能需要遍歷一個連結串列。

4、KMP演算法：

在一個字串中查詢是否包含目標的匹配字串。器主要思想是每趟比較過程讓字串先後滑動一個合適的位置，當發生不匹配的情況時，不是右移一位，而是移動（當前匹配的長度– 當前匹配子串的部分匹配值）位。

5、棧和佇列的共同特點是：只允許在端點處插入和刪除元素

6、棧通常採用線性儲存結構和連結串列儲存結構

7、在單鏈表中增加頭結點的目的是：方便運算的實現

8、設一棵二叉樹中有3個葉子結點，有8個度為1的結點，則該二叉樹中總共的結點數？

       葉子結點數=雙分支結點數+1

       所以總結點數為3+8+（3-1）=13

9、已知二叉樹後續遍歷序列是dabec,中序遍歷序列是debac,它的前序遍歷序列是：（cedba）

       （1）首先找根節點：後續的最後一個

       （2）然後找左右分支：根據中序

       （3）對左右分支迴圈使用上述方法

10、下列資料結構中具有記憶功能的是：C

       A.佇列    B.迴圈佇列    C 棧    D 順序表

       解析：具有記憶功能的資料結構是棧，原因很簡單：後進棧的先出棧，所以你對一個棧進行出棧操作，出來的元素肯定是你最後存入棧中的元素，所以棧有記憶功能。

11、遞迴演算法一般使用的資料結構是：棧

       解析：遞迴的過程就是壓棧的過程，先把資料壓進棧，遞迴結束時，再出棧。

12、簡述直接插入排序演算法

       （1）選擇原始序列中的第一個數，作為有序數列

（2）每次向後選取一個數據，插到已經有序的數列中的合適位置，查詢位置的方法是順序查詢

       （3）不斷重複第二步

13、折半插入排序

       插入的基本思想和直接插入排序類似，只是插入位置採用折半查詢法

14、希爾排序

       希爾排序又稱作縮小增量排序，本質還是插入排序：將待排序列按照選取得增量分成幾個子序列分別對這幾個子序列進行直接插入排序。

       注意：（1）增量序列的一個值一定是1

               （2）增量序列的值應儘量沒有除1之外的公因子

15、氣泡排序結束條件是一趟排序過程中沒有發生關鍵字的交換

16、簡單選擇排序：

       從頭至尾順序掃描序列，找出其中最小的關鍵字，和第一個關鍵字交換，接著從剩下的關鍵字中繼續這種選擇和交換，直至最終序列有序

17、堆排序：

       （1）什麼是堆？

       堆可以看成一棵完全二叉樹，這棵二叉樹滿足：任何一個非葉子結點的值都不大於（或不小於）其左右孩子結點的值。若父親大孩子小，稱為大頂堆；若父親小孩子大，則稱為小頂堆。

       （2）堆排序的思想：

       堆排序就是將序列調整為推，根據堆中根節點的值是最大（或是最小），就可以找到這個序列的最大值（或最小值），然後將找出的這個值交換到序列的最後（或最前），這樣有序關鍵字增加1個，無序關鍵字減少1個，對新的無序序列重複這樣的操作，就可以實現排序。

18、歸併排序：

       歸併排序可以看作一個分為治之的過程：先將整個序列分成兩半，對每一半分別進行歸併排序，得到兩個有序序列，然後將這兩個有序序列歸併成一個序列即可。

19、基數排序

       基數排序的思想是“多關鍵字排序”，分成兩種：

1. 最高位優先

即先按最高位拍成若干序列，再對每個子序列按次高位排序

1. 最低為優先

不必分成子序列，粉刺排序全體關鍵字都參與。最低位優先進行，不通過比較，而是通過“分配”和收集

20、查詢法

       （1）順序查詢法：

從表的一端開始，順序掃描線性表，依次將掃描的關鍵字與給定值k比較，若當前掃描的關鍵字與k相等，則查詢成功；若掃描結束後，仍未發現關鍵字等於k的記錄，則查詢失敗。

1. 折半查詢

折半查詢首先限定線性表是有序的，然後與線性表的中間位置的關鍵字比較，如果大於則再線上性表右邊比較，反之在左邊比較。直到子區間小於1

21、分塊查詢

       分塊查詢又稱為索引順序查詢：分塊查詢把線性表分成若干個塊，每一塊中的元素儲存順序是任意的，但是塊與塊之間必須按照關鍵字大小有序排列，即前一塊中的最大值關鍵字小於後一塊最小值關鍵字。

22、二叉排序樹

       二叉排序樹或者為空樹，或者是滿足一下性質的二叉樹：

1. 若它的左子樹不空，則左子樹上的所有關鍵字的值均小於根關鍵字的值
2. 若它的右子樹不空，則右子樹上的所有關鍵字的值均大於根關鍵字的值
3. 左右子樹又分別是二叉排序樹

23、平衡二叉樹（AVL樹）

       以樹中所有結點為根的左右子樹高度之差的絕對值不超過1的二叉排序樹。

24、B樹

B樹是平衡m叉查詢樹，但是限制更強，要求所有葉子結點在同一層。且節點數等於關鍵字數加1

       性質：下層結點內的關鍵字取值總是落在由上層結點關鍵字所劃分的區間內。

25、B+樹

       （1）n個關鍵字的結點含有n個分支（對應B樹n個關鍵字含有n+1個分支）

       （2）B+樹中葉子結點包含資訊，並且包含全部關鍵字，葉子結點引出的指標指向記錄

       （3）B+樹中非葉子結點僅起到索引的作用，不含有該關鍵字對用的記錄的儲存地址（B樹每個關鍵字對應一個記錄的儲存地址）

26、赫夫曼樹

       赫夫曼樹又叫作最優二叉樹，特點是帶權路徑最短

       構造赫夫曼樹的方法：

1. 首先選擇其中最小權值的兩點，構造一棵樹
2. 將新生成的樹的根節點和剩餘的結點間，在選擇兩個最小權值組成一棵樹
3. 重複上述步驟，直到只剩下最後一棵樹為止，這棵樹就是赫夫曼樹

27、深度優先搜尋遍歷

       基本思想：首先訪問出發點v，並將其標記為已訪問過，然後選取與v鄰接的未被訪問的任意一個頂點w，並訪問它；再選取與w鄰接的未被訪問的任一頂點並訪問，以此重複進行。當一個頂點所有的鄰接頂點都被訪問過時，則依次退回到最近被訪問過的頂點，若該頂點還有其他臨近頂點未被訪問，則從這些未被訪問的頂點中取一個並重復訪問過程。

28、過度優先搜尋遍歷

       基本思想：首先訪問起始頂點v，然後選取與v鄰接的全部頂點w1,……，wn進行訪問，再依次訪問與w1,……，wn鄰接的全部頂點（已經訪問過的除外），依次類推直到所有頂點都被訪問過為止。

29、最小生成樹

       （1）普里姆演算法

演算法思想：從圖中任意取出一個頂點，把它當成一棵樹，然後從與這棵樹相接的邊中選取一個最短（權值最小）的邊，並將這條邊及其所連線的頂點也併入這棵樹中，此時得到一棵有兩個頂點的樹，然後從與這棵樹相接的邊中選取一條最短的邊，並將這條邊及其所連頂點併入當前樹中，得到一棵有3個頂點的樹。以此類推，直到圖中所有頂點都併入樹中為止，此時得到的生成樹就是最小生成樹。

（2）克魯斯卡爾演算法

演算法思想：將圖中邊按照從小到大排序，然後從最小邊開始掃描各邊，並檢測當前邊是否為候選邊，即是否該邊的併入會構成迴路，如果不構成迴路，則將該邊併入當前樹中，直到所有邊都被檢測完為止。

30、最短路徑：

       （1）迪傑斯特拉演算法（求圖中某一頂點到其餘各頂點的最短路徑）

              演算法思想：設有兩個頂點集合S和T，集合S中存放圖中已找到最短路徑的頂點，集合T中存放圖中剩餘頂點。初始狀態時，集合S中只包含源點v0，然後不斷從集合T中選取到頂點v0路徑長度最短的頂點vu併入到集合S中。集合每併入一個新的頂點vu，都要修改頂點v0到集合T中頂點的最短路徑長度值。不斷重複此過程，直到集合T的頂點全部併入到S中為止。

       （2）弗洛伊德演算法（求圖中任意一對頂點間的最短路徑）

              演算法思想：過程略

31、AOV網（Activity on Vertex network 活動在頂點上的網）

       一種可以形象地反應出整個工程中各個活動之間的先後關係的有向圖：以頂點表示活動、以邊表示活動的先後次序且沒有迴路的有向圖。

32、拓撲排序核心演算法

       對一個有向無環圖G進行拓撲排序，是將G中所有頂點排成一個線性序列，使得圖中任意以對頂點u和v，若存在u到v的路徑，則拓撲排序序列中一定是u出現在v的前邊。

       操作步驟如下：

1. 從有向圖中選擇一個沒有前驅（入度為0）的頂點輸出；
2. 刪除1）中的頂點，並且刪除從該頂點出發的全部邊；
3. 重複上述兩步，直到剩餘的圖中不存在沒有前驅的頂點為止。

33、AOE網（Activity on Edge network）

       對比AOV網：

       兩者的共同點：都是有向無環圖

       兩者的不同點：AOE網的邊表示活動，邊有權值，邊代表活動持續的時間；頂點表示事件，事件是圖中新活動開始或者舊活動結束的標誌。AOV網頂點表示活動，邊無權值，邊代表活動之間的先後關係。

34、關鍵路徑核心演算法

       關鍵路徑：在AOE網中，從源點到匯點的所有路徑中，具有最大路徑長度的路徑稱為關鍵路徑。

       完成整個工程最短時間就是關鍵路徑長度所代表的時間。關鍵路徑上的活動稱為關鍵活動。

       關鍵路徑既代表了一個最短又代表了一個最長：

       因為一個任務完成所花費的時間取決於其中最耗時得那一部分，而最耗時的那一部分就是完成這個任務的最短時間。

35、解決雜湊衝突的方法：

雜湊表（Hash table，也叫散列表），是根據關鍵碼值(Key value)而直接進行訪問的資料結構。

雜湊衝突：就是根據key即經過一個函式f(key)得到的結果的作為地址去存放當前的key value鍵值對(這個是hashmap的存值方式)，但是卻發現算出來的地址上已經有人先來了。就是說這個地方要擠一擠啦。這就是所謂的hash衝突啦

1. 開放定址法

1. 線性探測法
2. 平方探測法
3. 偽隨機序列法

1. 拉鍊法

參考文章：