影象處理之直方圖處理

阿新 • • 發佈：2018-12-11

灰度級範圍為[0,L-1]的數字影象的直方圖是離散函式：

$h(r_{k}) = n_{k}$

其中 $r_{k}$ 是第k級灰度值( $r_{k}$ =k)， $n_{k}$ 是影象中灰度值為 $r_{k}$ 的畫素個數。

通常用MN表示的影象畫素的總數除它的每個分量 $n_{k}$ 來歸一化直方圖，即：

$p(r_{k}) = n_{k}/MN$

M和N分別是影象的行和列維數，k = 0,1,...,L-1。歸一化直方圖的所有分量和為1。

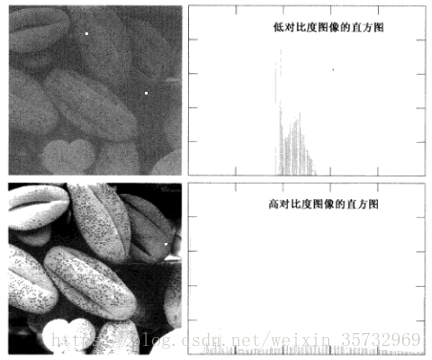
若一幅影象的畫素傾向於佔據整個可能的灰度級並且均勻分佈，則該影象會有高對比度的外觀和灰度細節豐富的特點。如下圖：

直方圖均衡

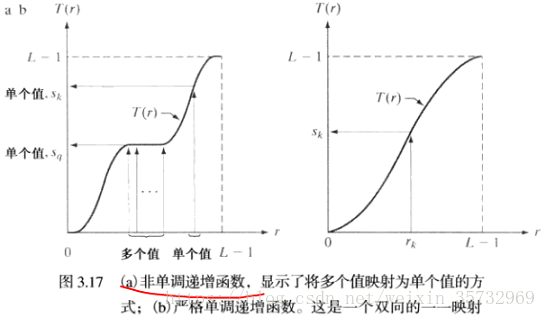
用變數r表示待處理的影象的灰度，灰度變換函式通常需要滿足兩個條件：

(a) T(r)在空間 $0\leqslant r\leqslant L-1$ 上為單調遞增函式
(b) 當 $0\leqslant r\leqslant L-1$ 時， $0\leqslant T(r)\leqslant L-1$

當考慮反函式 $r = T^{-1}(s),0\leqslant s\leqslant L-1$ 時，條件(a)改為：

(a') T(r)在空間 $0\leqslant r\leqslant L-1$

上是嚴格單調遞增函式

條件(a)保證輸出灰度值不少於相應的輸入值，防止灰度反變換時產生人為的缺陷；條件(b)保證輸出灰度的範圍與輸入灰度的範圍相同；條件(a')保證從s到r的反對映是單值的，即一對一的，防止出現二義性。如下圖：

為了產生均衡的直方圖，使用如下的灰度變換函式：

$s = T(r) = (L-1)\int_{0}^{r}p_{r}(w)dw$ ....................................(1)

容易看出，該變換滿足條件a和b。

下面解釋為什麼經過(1)式的灰度變換能產生均衡直方圖。

令 $p_{r}(r)$ 和 $p_{s}(s)$ 分別表示隨機變數r和s的概率密度函式(PDF)。若 $p_{r}(r)$ 和T(r)已知，則變換後的變數s的PDF為：

$p_{s}(s) = p_{r}(r)|dr/ds|$ ......................................................(2)

使用(1)式的變換函式，得：

$\frac{ds}{dr} = \frac{dT(r)}{dr} = (L-1)\frac{d}{dr}[\int_{0}^{r}p_{r}(w)dw] = (L-1)p_{r}(r)$

將dr/ds代入(2)式，得：

$p_{s}(s) = p_{r}(r)|dr/ds| = p_{r}(r)\left | \frac{1}{(L-1)p_{r}(r)} \right | = \frac{1}{L-1},0\leqslant s\leqslant L-1$

可知， $p_{s}(s)$ 始終是一個均勻概率密度函式，與 $p_{r}(r)$ 的形式無關。所以，經過(1)式灰度變換的影象能產生均衡直方圖。

(1)式的積分形式針對的是連續灰度值，而對於離散值，用求和的形式處理。一幅影象中灰度級 $r_{k}$ 出現的概率為：

$p(r_{k}) = n_{k}/MN,k = 0,1,2,...,L-1$

(1)式中變換的離散形式為：

$s_{k} = T(r_{k}) = (L-1)\sum_{j=0}^{k}p_{r}(r_{j}) = \frac{(L-1)}{MN}\sum_{j=0}^{k}n_{j},k = 0,1,2,...,L-1$

注：在實際使用中，需要將灰度值取近似為最接近的整數。

直方圖匹配（規定化）

直方圖匹配或直方圖規定化，是指處理後的影象具有規定的直方圖形狀。

具體說來就是，要找到一個灰度變換函式，使影象在該灰度變換函式的作用下，產生一個我們指定形狀的直方圖，所謂指定形狀的直方圖形狀，其實就是一個指定的概率密度函式。

假設r和z分別表示輸入影象和輸出影象的灰度級， $p_{r}(r)$ 是輸入影象的概率密度函式， $p_{z}(z)$ 是我們希望輸出影象所具有的指定概率密度函式。

令：

$s = T(r) = (L-1)\int_{0}^{r}p_{r}(w)dw$

可以看出，這就是直方圖均衡中的變換函式。知道 $p_{r}(r)$ ，就能得到T(r)。

定義隨機變數z：

$G(z) = (L-1)\int_{0}^{z}p_{z}(t)dt = s$

同樣，知道 $p_{z}(z)$ ，就能得到G(z)，而 $p_{z}(z)$ 就是我們指定的概率密度函式。

可得：

$z = G^{-1}[T(r)] = G^{-1}(s)$

上式就是我們要求的直方圖匹配的灰度變換函式。

對於離散形式，類似的我們令：

$s_{k} = T(r_{k}) = (L-1)\sum_{j=0}^{k}p_{r}(r_{j}) = \frac{(L-1)}{MN}\sum_{j=0}^{k}n_{j},k = 0,1,2,...,L-1$

$G(z_{q}) = (L-1)\sum_{i=0}^{q}p_{z}(z_{i})=s_{k},q=0,1,2,...,L-1$

其中， $p_{z}(z_{i})$ 規定的直方圖的第i個值， $z_{q}$ 是規定的直方圖對應的影象的第q級灰度值（ $z_{q}$ =q），利用反變換找到期望的 $z_{q}$ ：

$z_{q} = G^{-1}(s_{k})$

實踐中，並不需要反變換。因為我們處理的灰度級是整數（如8位元影象的灰度級是從0到255），我們常用下面的直方圖規定化過程：

計算給定影象的 $p_{r}(r)$ 及其直方圖均衡變換 $s_{k}$ ，把 $s_{k}$ 四捨五入為範圍[0,L-1]內的整數；
對q=0,1,2,...,L-1計算 $G(z_{q})$ ，其中 $p_{z}(z_{i})$ 規定的直方圖的值，把G四捨五入為範圍[0,L-1]內的整數，將G存在一個表中；
對每一個 $s_{k}$ ，k=0,1,2,...,L-1，從步驟2中儲存的G值表中尋找 $G(z_{q})$ 使 $G(z_{q})$ 最接近 $s_{k}$ 。例如表中第64個 $G(z_{q})$ 最接近 $s_{k}$ ，則根據 $G(z_{q})$ 的定義，此時q=63，也就是 $z_{q}$ =63。當滿足給定 $s_{k}$ 的 $z_{q}$ 值多於一個時，按慣例選擇最小的值。

參考資料：岡薩雷斯《數字影象處理》

影象處理之直方圖處理

灰度級範圍為[0,L-1]的數字影象的直方圖是離散函式：其中是第k級灰度值(=k)，是影象中灰度值為的畫素個數。通常用MN表示的影象畫素的總數除它的每個分量來歸一化直方圖，即： M和N分別是影象的行和列維數，k = 0,1,...,L-1。歸一化直方圖的所有

數字影象處理之直方圖均衡化（Octave)

直方圖的均衡化是什麼呢？舉個簡單的例子：在一個圓中有很多石頭，都集中在圓心附近，對其均衡化就是讓這些石頭儘可能的均勻分佈在圓這個區域內。並且還有一個原則：如果石頭A在原來狀態下距離圓心的距離在所有石頭是第4位，那麼均衡化後仍然是第4位，相對順序不能變。（大概就是一個拉的更寬了）

影象處理之直方圖均衡MATLAB程式碼實現

MATLAB畫灰度影象直方圖的程式碼 I=imread('cameraman.tif'); [M N]=size(I);%求出圖片大小 y=zeros(1,256) x=0:255; for t=0:255 for i=1:M for j=1:N

紅外影象處理之直方圖均衡的matlab原始碼與效果驗證

紅紅外影象是熱輻射成像，由於場景中的目標與背景的溫差相對較小，紅外影象的動態範圍大、對比度低，信噪比也較可見光影象的低。為了能夠從紅外影象中正確地識別出目標，必須對紅外影象進行增強處理。一般紅外探測器的效能區分於材料，氧化釩等高階的靈敏度高相應的價格較貴，多晶矽的一般靈敏度要

《數字影象處理》--直方圖處理

直方圖灰度直方圖是灰度級的函式，描述的是影象中具有該灰度級的像元的個數。確定影象像元的灰度值範圍，以適當的灰度間隔為單位將其劃分為若干等級，以橫軸表示灰度級，以縱軸表示每一灰度級具有的像元數或該像元數佔總像元數的比例值，做出的條形統計圖即為灰度直方圖。如

【數字影象處理】直方圖處理

灰度直方圖灰度直方圖是灰度級的函式，描述的是影象中具有該灰度級的像元的個數。確定影象像元的灰度值範圍，以適當的灰度間隔為單位將其劃分為若干等級，以橫軸表示灰度級，以縱軸表示每一灰度級具有的像元數或該像元數佔總像元數的比例值，做出的條形統計圖即為灰度直方圖。如下圖所示，做直方圖

Java 異常處理之捕獲處理流程

package com.exception2; /* * 注意: 1. 當異常發生的時候,程式會終止,其後面的程式碼不會執行. 2. 異常分為編譯時異常和執行期異常編譯期異常必須用 try{}catch{}捕獲,執行期異常可以不捕獲編譯期異常從 Except

影象增強之直方圖均衡化（不用histeq）與直方圖規定化

histeq 是MATLAB裡面直方圖均衡化的函式，這裡我們不用它手動實現直方圖均衡化，以加深對影象直方圖均衡化操作的理解。前些天數字影象處理課上老師留了一個作業，要求自選一副影象對其做直方圖均衡化處理，然後對影象進行灰度變換，使變換後的影象大致具有下圖所示歸一化直方圖的

Spring 異常處理之全域性處理

承接上文Spring異常處理之本地處理，本文介紹spring異常處理的第三種方式，也就是全域性處理。為什麼將該方式取名為全域性處理，其實很簡單，因為該方式本質上和本地處理是一樣的，無非就是本地處理將異常處理方法或者說異常處理邏輯直接寫在controller中，而

影象分析之直方圖分析

- created by gloomyfish 影象分析之強度直方圖分析直方圖介紹強度直方圖圖形化顯示不同的畫素值在不同的強度值上的出現頻率，對於灰度影象來說強度範圍為[0~255]之間，對於RGB的彩色影象可以獨立顯示三種顏色的強度直方圖。強度直方

Spring 異常處理之本地處理

承接上文Spring 異常處理之 HTTP 狀態碼，本文介紹spring異常處理的第二種方式。為什麼說這種異常處理方式叫本地處理，因為該方式是在Controller內部處理該Controller中的方法丟擲的異常。需要注意的是，這種方式其實還可以細分為3種。具

Salesforce LWC學習(十) 前端處理之 list 處理

本篇參看：https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/Array list是我們經常要處理的內容，lwc前端針對list主要有幾個函式處理，不同函式針對不同場景有不同的功能。下面就根據幾個常用

影象處理學習筆記之直方圖的計算與繪製

影象直方圖包含豐富的影象細節資訊，反映了影象畫素點的概率分佈情況，它統計了每一個強度值具有的畫素個數。灰度級範圍是[0,L-1]的數字影象的直方圖是離散函式h(rk)=nk,其中是rk第k級灰度值，nk是影象中灰度為rk的畫素個數。在實踐中，經常用乘積MN表示的影象畫素總數

視訊、圖形影象處理之Opencv技術記錄（六）、均衡直方圖

目標在本教程中，您將學習：什麼是影象直方圖以及為什麼它有用理論什麼是影象直方圖？它是影象強度分佈的圖形表示。它量化了所考慮的每個強度值的畫素數。什麼是直方圖均衡？

轉《影象處理之表面濾波》

本文介紹經典的表面模糊Surface Blur演算法與實現。表面模糊是PS裡一個重要的保邊濾波器，它的演算法很簡單，公式如下所示：主要思想還是計算當前畫素X的鄰域範圍內不同畫素的加權求和，邊緣地方的畫素，加權比較大，平滑的地方加權比較小，以此來保留邊緣資訊，平滑平坦區域；效果如下圖所示：

影象處理之---光流法

LK光流演算法公式詳解：由於工程需要用到 Lucas-Kanade 光流，在此進行一下簡單整理（後續還會陸續整理關於KCF，PCA，SVM，最小二乘、嶺迴歸、核函式、dpm等等）：光流，簡單說也就是畫面移動過程中，影象上每個畫素的x，y位移量，比如第t幀的時候A點的位置是(x1,

影象處理之積分圖應用四（基於區域性均值的影象二值化演算法）

影象處理之積分圖應用四（基於區域性均值的影象二值化演算法）基本原理均值法，選擇的閾值是區域性範圍內畫素的灰度均值(gray mean)，該方法的一個變種是用常量C減去均值Mean，然後根據均值實現如下操作： pixel = (pixel > (mean - c)) ? ob

影象處理之積分圖應用三（基於NCC快速相似度匹配演算法）

影象處理之積分圖應用三（基於NCC快速相似度匹配演算法）基於Normalized cross correlation(NCC)用來比較兩幅影象的相似程度已經是一個常見的影象處理手段。在工業生產環節檢測、監控領域對物件檢測與識別均有應用。NCC演算法可以有效降低光照對影象比較結果的影響。而

影象處理之積分圖應用二(快速邊緣保留濾波演算法)

影象處理之積分圖應用二(快速邊緣保留濾波演算法) 一：基本原理傳統的影象邊緣保留濾波演算法-如高斯雙邊模糊、Mean-Shift模糊等計算複雜、效率比較低，雖然有各種手段優化或者快速計算方法，當時演算法相對一般碼農來說理解起來比較費勁，不是一個的選擇，而通過積分影象實現區域性均方差

影象處理之積分圖應用一(半徑無關的快速模糊演算法)

影象處理之積分影象應用一(半徑無關的快速模糊演算法) 一：基本原理概述傳統的影象空間域卷積模糊演算法，當視窗大小改變時卷積模糊時間也會變化，而且隨著視窗尺寸越大計算量也越大，演算法執行時間約越長。在很多時候無法滿足實時性要求。而基於積分影象可以實現對視窗區域和大小的快速計算，把傳統卷積