嗶哩嗶哩2018.9.21筆試 小A最多會新認識多少人
阿新 • • 發佈:2018-12-11
題目描述
小A參加一個n人的活動,每個人都有一個編號(0<=i<=n-1),其中有m對相互認識,在活動中兩個人可以通過互相都認識都認識的一個人介紹認識。現在問活動結束後,小A最多會新認識多少人? 輸入: 第一行是聚會人數n 第二行是小A的編號a 接下來m行為互相認識的對,以’,'分割 輸出: 小A最多會新認識多少人的人數。 樣例輸入: 7 5 6 1,0 3,1 4,1 5,3 6,1 6,5 樣例輸出: 3 提示: 小A新認識的人為【0,1,4】
深度遍歷
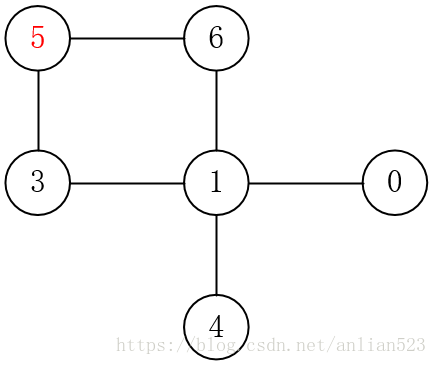
2.該問題是一個無向圖的深度遍歷。
3.在深度遍歷的過程中,把小A新認識的人加入一個集合中,最後輸出這個集合的長度。
4.注意不要把小A和小A初始已經認識的朋友加入集合中
5.考慮到整個圖可能是不連通的,所以必須從a開始進行深度遍歷
n = eval(input())
a = eval(input())
m = eval(input())
from collections import defaultdict
d = defaultdict(list)
for i in range(m):
start,end = map(int,input().split(','))
d[start].append(end) 但該程式碼中,有些遞迴分支會作一些無用功,因為可能會深度遍歷到小A的初始朋友中去。比如,假設遞迴初始從5到了3,在這之後的遞迴分支,程式會遞迴到6去,但6是小A的初始朋友,則遞迴不應該遞迴到6。所以上述程式碼還可以優化。
深度遍歷+層次圖
利用層次圖的思想,起碼節點5的層次為0,那麼3和6的層次為1,1的層次為2,以此類推。
所以,當我們遍歷到層次為1的節點時,其他同樣層次為1的節點的visited也應該設定為True,這樣就能克服之前程式碼的缺點,避免遞迴走到小A的初始朋友。
n = eval(input())
a = eval(input())
m = eval(input())
from collections import defaultdict
d = defaultdict(list)
for i in range(m):
start,end = map(int,input().split(','))
d[start].append(end)
d[end].append(start)
visited = [False]*n
visited[a] = True
newfriend = set()
def mark(li):
for i in li:
visited[i] = True
def antiMark(li):
for i in li:
visited[i] = False
def recur(i,step):
if step >= 2:
newfriend.add(i)
if (d[i] == []):
return
for re in d[i]:
if visited[re] == False:
if step == 0:
mark(d[i])
visited[re] = True
recur(re,step+1)
visited[re] = False
if step == 0:
antiMark(d[i])
recur(a,0)
print(len(newfriend))
mark函式用來標記層次為1的節點為True,antiMark函式用來當遞迴返回時反標記層次為1的節點。 另外,遞迴函式第二個引數step代表遞迴的深度,當遞迴的step>=2時,那麼此時的i肯定是新認識的朋友。

