【轉】Bloom Filter 布隆濾波器
在日常生活中,包括在設計計算機軟體時,我們經常要判斷一個元素是否在一個集合中。
比如在字處理軟體中,需要檢查一個英語單詞是否拼寫正確(也就是要判斷 它是否在已知的字典中);在 FBI,一個嫌疑人的名字是否已經在嫌疑名單上;在網路爬蟲裡,一個網址是否被訪問過等等。最直接的方法就是將集合中全部的元素存在計算機中,遇到一個新 元素時,將它和集合中的元素直接比較即可。一般來講,計算機中的集合是用雜湊表(hash table)來儲存的。它的好處是快速準確,缺點是費儲存空間。當集合比較小時,這個問題不顯著,但是當集合巨大時,雜湊表儲存效率低的問題就顯現出來 了。比如說,一個象 Yahoo,Hotmail 和 Gmai 那樣的公眾電子郵件(email)提供商,總是需要過濾來自發送垃圾郵件的人(spamer)的垃圾郵件。一個辦法就是記錄下那些發垃圾郵件的 email 地址。由於那些傳送者不停地在註冊新的地址,全世界少說也有幾十億個發垃圾郵件的地址,將他們都存起來則需要大量的網路伺服器。如果用雜湊表,每儲存一億 個 email 地址, 就需要 1.6GB 的記憶體(用雜湊表實現的具體辦法是將每一個 email 地址對應成一個八位元組的資訊指紋(詳見:googlechinablog.com/2006/08/blog-post.html), 然後將這些資訊指紋存入雜湊表,由於雜湊表的儲存效率一般只有 50%,因此一個 email 地址需要佔用十六個位元組。一億個地址大約要 1.6GB, 即十六億位元組的記憶體)。因此存貯幾十億個郵件地址可能需要上百 GB 的記憶體。除非是超級計算機,一般伺服器是無法儲存的。(該段引用谷歌數學之美:http://www.google.com.hk/ggblog/googlechinablog/2007/07/bloom-filter_7469.html)
一、基本概念
布隆過濾器(Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的。它實際上是由一個很長的二進位制向量和一系列隨機對映函式組成,布隆過濾器可以用於檢索一個元素是否在一個集合中。它的優點是空間效率和查詢時間都遠遠超過一般的演算法,缺點是有一定的誤識別率(假正例False positives,即Bloom Filter報告某一元素存在於某集合中,但是實際上該元素並不在集合中)和刪除困難,但是沒有識別錯誤的情形(即假反例False negatives,如果某個元素確實沒有在該集合中,那麼Bloom Filter 是不會報告該元素存在於集合中的,所以不會漏報)。
如果想判斷一個元素是不是在一個集合裡,一般想到的是將所有元素儲存起來,然後通過比較確定。連結串列,樹等等資料結構都是這種思路. 但是隨著集合中元素的增加,我們需要的儲存空間越來越大,檢索速度也越來越慢。不過世界上還有一種叫作散列表(又叫雜湊表,Hash table)的資料結構。它可以通過一個Hash函式將一個元素對映成一個位陣列(Bit Array)中的一個點。這樣一來,我們只要看看這個點是不是 1 就知道可以集合中有沒有它了。這就是布隆過濾器的基本思想。
Hash面臨的問題就是衝突。假設 Hash 函式是良好的,如果我們的位陣列長度為 m 個點,那麼如果我們想將衝突率降低到例如 1%, 這個散列表就只能容納 m/100 個元素。顯然這就不叫空間有效了(Space-efficient)。解決方法也簡單,就是使用多個 Hash,如果它們有一個說元素不在集合中,那肯定就不在。如果它們都說在,雖然也有一定可能性它們在說謊,不過直覺上判斷這種事情的概率是比較低的。
優點
相比於其它的資料結構,布隆過濾器在空間和時間方面都有巨大的優勢。布隆過濾器儲存空間和插入/查詢時間都是常數。另外, Hash 函式相互之間沒有關係,方便由硬體並行實現。布隆過濾器不需要儲存元素本身,在某些對保密要求非常嚴格的場合有優勢。
布隆過濾器可以表示全集,其它任何資料結構都不能;
k 和 m 相同,使用同一組 Hash 函式的兩個布隆過濾器的交併差運算可以使用位操作進行。
缺點
但是布隆過濾器的缺點和優點一樣明顯。誤算率(False Positive)是其中之一。隨著存入的元素數量增加,誤算率隨之增加。但是如果元素數量太少,則使用散列表足矣。
另外,一般情況下不能從布隆過濾器中刪除元素. 我們很容易想到把位列陣變成整數陣列,每插入一個元素相應的計數器加1, 這樣刪除元素時將計數器減掉就可以了。然而要保證安全的刪除元素並非如此簡單。首先我們必須保證刪除的元素的確在布隆過濾器裡面. 這一點單憑這個過濾器是無法保證的。另外計數器迴繞也會造成問題。
二、演算法描述
一個empty bloom filter是一個有m bits的bit array,每一個bit位都初始化為0。並且定義有k個不同的hash function,每個都以uniform random distribution將元素hash到m個不同位置中的一個。在下面的介紹中n為元素數,m為布隆過濾器或雜湊表的slot數,k為布隆過濾器重hash function數。
為了add一個元素,用k個hash function將它hash得到bloom filter中k個bit位,將這k個bit位置1。
為了query一個元素,即判斷它是否在集合中,用k個hash function將它hash得到k個bit位。若這k bits全為1,則此元素在集合中;若其中任一位不為1,則此元素比不在集合中(因為如果在,則在add時已經把對應的k個bits位置為1)。
不允許remove元素,因為那樣的話會把相應的k個bits位置為0,而其中很有可能有其他元素對應的位。因此remove會引入false negative,這是絕對不被允許的。
當k很大時,設計k個獨立的hash function是不現實並且困難的。對於一個輸出範圍很大的hash function(例如MD5產生的128 bits數),如果不同bit位的相關性很小,則可把此輸出分割為k份。或者可將k個不同的初始值(例如0,1,2, … ,k-1)結合元素,feed給一個hash function從而產生k個不同的數。
當add的元素過多時,即n/m過大時(n是元素數,m是bloom filter的bits數),會導致false positive過高,此時就需要重新組建filter,但這種情況相對少見。
三、 時間和空間上的優勢
當可以承受一些誤報時,布隆過濾器比其它表示集合的資料結構有著很大的空間優勢。例如self-balance BST, tries, hash table或者array, chain,它們中大多數至少都要儲存元素本身,對於小整數需要少量的bits,對於字串則需要任意多的bits(tries是個例外,因為對於有相同prefixes的元素可以共享儲存空間);而chain結構還需要為儲存指標付出額外的代價。對於一個有1%誤報率和一個最優k值的布隆過濾器來說,無論元素的型別及大小,每個元素只需要9.6 bits來儲存。這個優點一部分繼承自array的緊湊性,一部分來源於它的概率性。如果你認為1%的誤報率太高,那麼對每個元素每增加4.8 bits,我們就可將誤報率降低為原來的1/10。add和query的時間複雜度都為O(k),與集合中元素的多少無關,這是其他資料結構都不能完成的。
如果可能元素範圍不是很大,並且大多數都在集合中,則使用確定性的bit array遠遠勝過使用布隆過濾器。因為bit array對於每個可能的元素空間上只需要1 bit,add和query的時間複雜度只有O(1)。注意到這樣一個雜湊表(bit array)只有在忽略collision並且只儲存元素是否在其中的二進位制資訊時,才會獲得空間和時間上的優勢,而在此情況下,它就有效地稱為了k=1的布隆過濾器。
而當考慮到collision時,對於有m個slot的bit array或者其他雜湊表(即k=1的布隆過濾器),如果想要保證1%的誤判率,則這個bit array只能儲存m/100個元素,因而有大量的空間被浪費,同時也會使得空間複雜度急劇上升,這顯然不是space efficient的。解決的方法很簡單,使用k>1的布隆過濾器,即k個hash function將每個元素改為對應於k個bits,因為誤判度會降低很多,並且如果引數k和m選取得好,一半的m可被置為為1,這充分說明了布隆過濾器的space efficient性。
四、 舉例說明
以垃圾郵件過濾中黑白名單為例:現有1億個email的黑名單,每個都擁有8 bytes的指紋資訊,則可能的元素範圍為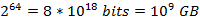 ,對於bit array來說是根本不可能的範圍,而且元素的數量(即email列表)為
,對於bit array來說是根本不可能的範圍,而且元素的數量(即email列表)為 ![clip_image002[6]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318585390.png) ,相比於元素範圍過於稀疏,而且還沒有考慮到雜湊表中的collision問題。
,相比於元素範圍過於稀疏,而且還沒有考慮到雜湊表中的collision問題。
若採用雜湊表,由於大多數採用open addressing來解決collision,而此時的search時間複雜度為![clip_image002[8]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318595880.png) 。即若雜湊表半滿(n/m = 1/2),則每次search需要probe 2次,因此在保證效率的情況下雜湊表的儲存效率最好不超過50%。此時每個元素佔8 bytes,總空間為:
。即若雜湊表半滿(n/m = 1/2),則每次search需要probe 2次,因此在保證效率的情況下雜湊表的儲存效率最好不超過50%。此時每個元素佔8 bytes,總空間為: ![clip_image002[6]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318585390.png) 。若採用Perfect hashing(這裡可以採用Perfect hashing是因為主要操作是search/query,而並不是add和remove),雖然保證worst-case也只有一次probe,但是空間利用率更低,一般情況下為50%,worst-case時有不到一半的概率為25%。
。若採用Perfect hashing(這裡可以採用Perfect hashing是因為主要操作是search/query,而並不是add和remove),雖然保證worst-case也只有一次probe,但是空間利用率更低,一般情況下為50%,worst-case時有不到一半的概率為25%。
若採用布隆過濾器,取k=8。因為n為1億,所以總共需要 ![clip_image002[12]](http://images.cnblogs.com/cnblogs_com/allensun/201102/20110216231900208.png) 被置位為1,又因為在保證誤判率低且k和m選取合適時,空間利用率為50%(後面會解釋),所以總空間為:
被置位為1,又因為在保證誤判率低且k和m選取合適時,空間利用率為50%(後面會解釋),所以總空間為:![clip_image002[10]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318599402.png) 。所需空間比上述雜湊結構小得多,並且誤判率在萬分之一以下。
。所需空間比上述雜湊結構小得多,並且誤判率在萬分之一以下。
五、誤判概率的證明和計算
假設布隆過濾器中的hash function滿足simple uniform hashing假設:每個元素都等概率地hash到m個slot中的任何一個,與其它元素被hash到哪個slot無關。若m為bit數,則對某一特定bit位在一個元素由某特定hash function插入時沒有被置位為1的概率為:
則k個hash function中沒有一個對其置位的概率為:
如果插入了n個元素,但都未將其置位的概率為:
則此位被置位的概率為:
現在考慮query階段,若對應某個待query元素的k bits全部置位為1,則可判定其在集合中。因此將某元素誤判的概率為:
從上式中可以看出,當m增大或n減小時,都會使得誤判率減小,這也符合直覺。
現在計算對於給定的m和n,k為何值時可以使得誤判率最低。設誤判率為k的函式為:
下面求最值
可以看出若要使得誤判率≤1/2,則:
這說明了若想保持某固定誤判率不變,布隆過濾器的bit數m與被add的元素數n應該是線性同步增加的。
六、設計和應用布隆過濾器的方法
應用時首先要先由使用者決定要add的元素數n和希望的誤差率P。這也是一個設計完整的布隆過濾器需要使用者輸入的僅有的兩個引數,之後的所有引數將由系統計算,並由此建立布隆過濾器。
系統首先要計算需要的記憶體大小m bits:
再由m,n得到hash function的個數:
至此係統所需的引數已經備齊,接下來add n個元素至布隆過濾器中,再進行query。
根據公式,當k最優時:
因此可驗證當P=1%時,儲存每個元素需要9.6 bits:
而每當想將誤判率降低為原來的1/10,則儲存每個元素需要增加4.8 bits:
這裡需要特別注意的是,9.6 bits/element不僅包含了被置為1的k位,還把包含了沒有被置為1的一些位數。此時的
才是每個元素對應的為1的bit位數。
此概率為某bit位在插入n個元素後未被置位的概率。因此,想保持錯誤率低,布隆過濾器的空間使用率需為50%。
![clip_image002[10]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318599402.png)
七、Bloom Filter 用例
Google 著名的分散式資料庫 Bigtable 使用了布隆過濾器來查詢不存在的行或列,以減少磁碟查詢的IO次數[3]。
Squid 網頁代理快取伺服器在 cache digests 中使用了也布隆過濾器[4]。
Venti 文件儲存系統也採用布隆過濾器來檢測先前儲存的資料[5]。
SPIN 模型檢測器也使用布隆過濾器在大規模驗證問題時跟蹤可達狀態空間[6]。
Google Chrome瀏覽器使用了布隆過濾器加速安全瀏覽服務[7]。
在很多Key-Value系統中也使用了布隆過濾器來加快查詢過程,如 Hbase,Accumulo,Leveldb,一般而言,Value 儲存在磁碟中,訪問磁碟需要花費大量時間,然而使用布隆過濾器可以快速判斷某個Key對應的Value是否存在,因此可以避免很多不必要的磁碟IO操作,只是引入布隆過濾器會帶來一定的記憶體消耗,下圖是在Key-Value系統中布隆過濾器的典型使用:

八、布隆過濾器相關擴充套件
Counting filters
基本的布隆過濾器不支援刪除(Deletion)操作,但是 Counting filters 提供了一種可以不用重新構建布隆過濾器但卻支援元素刪除操作的方法。在Counting filters中原來的位陣列中的每一位由 bit 擴充套件為 n-bit 計數器,實際上,基本的布隆過濾器可以看作是隻有一位的計數器的Counting filters。原來的插入操作也被擴充套件為把 n-bit 的位計數器加1,查詢操作即檢查位陣列非零即可,而刪除操作定義為把位陣列的相應位減1,但是該方法也有位的算術溢位問題,即某一位在多次刪除操作後可能變成負值,所以位陣列大小 m 需要充分大。另外一個問題是Counting filters不具備伸縮性,由於Counting filters不能擴充套件,所以需要儲存的最大的元素個數需要提前知道。否則一旦插入的元素個數超過了位陣列的容量,false positive的發生概率將會急劇增加。當然也有人提出了一種基於 D-left Hash 方法實現支援刪除操作的布隆過濾器,同時空間效率也比Counting filters高。
Data synchronization
Byers等人提出了使用布隆過濾器近似資料同步[9]。
Bloomier filters
Chazelle 等人提出了一個通用的布隆過濾器,該布隆過濾器可以將某一值與每個已經插入的元素關聯起來,並實現了一個關聯陣列Map[10]。與普通的布隆過濾器一樣,Chazelle實現的布隆過濾器也可以達到較低的空間消耗,但同時也會產生false positive,不過,在Bloomier filter中,某 key 如果不在 map 中,false positive在會返回時會被定義出的。該Map 結構不會返回與 key 相關的在 map 中的錯誤的值。
在下一節,我們將會用Java 實現一個簡單的 BloomFilter.
本文圖片和內容文字來源與兩篇文章,原文地址:

![clip_image002[16]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319014536.png)
![clip_image002[18]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319024470.png)
![clip_image002[20]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319021057.png)
![clip_image002[22]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319026007.png)
![clip_image002[24]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319039321.png)
![clip_image002[26]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319043367.png)
![clip_image002[28]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319045809.png)
![clip_image002[30]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319058775.png)
![clip_image002[32]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319062089.png)
![clip_image002[34]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319061466.png)
![clip_image002[36]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319075.png)
![clip_image002[38]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319071367.png)
![clip_image002[40]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319087921.png)
![clip_image002[42]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319093395.png)
![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319091169.png)
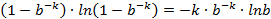
![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319101070.png)
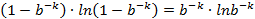
![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319117591.png)
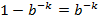
![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319127492.png)
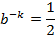
![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319136280.png)

![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319143673.png)
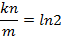
![clip_image002[44]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319159637.png)
![clip_image002[52]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319164554.png)
![clip_image002[54]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319171980.png)
![clip_image002[56]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319184946.png)
![clip_image002[58]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319181848.png)
![clip_image002[60]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319199274.png)
![clip_image002[52]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319207779.png)
![clip_image002[66]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319219076.png)
![clip_image004[8]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319227515.png)
![clip_image002[70]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319233238.png)
![clip_image002[72]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319248156.png)
![clip_image002[74]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319257533.png)
![clip_image002[76]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319256072.png)
![clip_image002[78]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319266562.png)
![clip_image002[80]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319269877.png)
![clip_image002[82]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319272003.png)