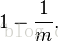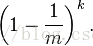寫在前面

在大數據與雲計算發展的時代，我們經常會碰到這樣的問題。我們是否能高效的判斷一個用戶是否訪問過某網站的主頁（每天訪問量上億）或者需要統計網站的pv、uv。最直接的想法是將所有的訪問者存起來，然後每次用戶訪問的時候與之前集合進行比較。不管是將訪問信息存在內存（或數據庫）都會對服務器造成非常大的壓力。那是否存在一種方式，容忍一定的錯誤率，高效（計算復雜度、空間復雜度）的實現訪問量信息的跟蹤、統計呢？接下來介紹的布隆過濾器（BloomFilter）就可以滿足當前的使用場景（註釋：基數計數法同樣能滿足pv、uv的統計）。

布隆過濾器簡介

布隆過濾器（BloomFilter）是1970年由布隆提出的一種空間空間效率很高的隨機數據結構，它利用位數組很簡潔地表示一個集合，並判斷一個元素是否屬於這個集合。使用布隆過濾器，存在第一類出錯（Falsepositive），但是不會存在第二類錯誤（Falsenegative），因此，布隆過濾器擁有100%的召回率。也就是說，布隆過濾器能夠準確判斷一個元素不在集合內，但只能判斷一個元素可能在集合內。因此，BloomFilter不適合“零錯誤”的應用場合。在能夠容忍低錯誤的應用場合下，BloomFilter通過極少的錯誤換取了存儲空間的極大節省。我們可以向布隆過濾器裏添加元素，但是不能從中移除元素（普通布隆過濾器，增強的布隆過濾器是可以移除元素的）。隨著布隆過濾器中元素的增加，犯第一類錯誤的可能性也隨之增大。

算法描述

一個空的布隆過濾器有長度為M比特的bit數組構成，且所有位都初始化0。一個元素通過K個不同的hash函數隨機散列到bit數組的K個位置上，K必須遠小於M。K和M的大小由錯誤率（falsepositiverate）決定。

Bloom Filter的一個例子集合S｛x，y，z｝。帶有顏色的箭頭表示元素經過k（k＝3）hash函數的到在M（bit數組）中的位置。元素W不在S集合中，因為元素W經過k個hash函數得到在M（bit數組）的k個位置中存在值為0的位置。

向集合S中添加元素x：x經過k個散列函數後，在M中得到k個位置，然後，將這k個位置的值設置為1。

判斷x元素是否在集合S中：x經過k個散列函數後，的到k個位置的值，如果這k個值中間存在為0的，說明元素x不在集合中——元素x曾經插入到過集合S，則M中的k個位置會全部置為1；如果M中的k個位置全為1，則有兩種情形。情形一：這個元素在這個集合中；情形二：曾經有元素插入的時候將這k個位置的值置為1了（第一類錯誤產生的原因FalsePositive）。簡單的布隆過濾器無法區分這兩種情況，在增強版中解決了這個問題。

設計k個相互獨立的hash函數可能工作量比較大，但是一個好的hash函數是降低誤判率的關鍵。一個良好的hash函數應該有寬輸出，他們之間的沖突應盡量低，這樣k個hash函數能靜可能的將值hash的更多的位置。hash函數的設計是我們可以將k個不同的值（ 0, 1, ..., k ? 1）作為參數傳入，或者將它們加入主鍵中。對於大的M或者k，hash函數之間的獨立性對誤判率影響非常大（(Dillinger & Manolios (2004a),Kirsch & Mitzenmacher (2006))）,Dillinger在k個散列函數中，多次使用同一個函數散列，分析對誤判率的影響。

對於簡單布隆過濾器來說，從集合S中移除元素x是不可能的，且falsenegatives不允許。元素散列到k個位置，盡管可以 將這k個位置的值置為0來移除這個元素，但是這同事也移除了那些散落後，有值落在這k位中的元素。因此，沒有一種方法可以判斷移除這個元素後是否影響其它已經加入集合中的元素，將k個位置置為0會引入二類誤差（falsenegative）。

時間復雜度和空間復雜度

在falsepositives的情況下，布隆過濾器相比其它的集合（平衡二叉樹、樹、hash表、數組、鏈表）只需要少量的存儲空間。布隆過濾器的添加和檢查元素是否在集合內的復雜度為O(K)。Hash表的平均復雜度比布隆過濾器更低。Bloom過濾器在誤差最優的情況下，平均每個元素大概是1.44bit。

錯誤率估計

布隆過濾器判斷一個元素是否屬於它表示的集合時會存在已定的錯誤率（falsepositiverate），接下來就估計錯誤率的大小。在估計誤差前，我們假設kn<m(k哈希函數的個數，n集合中元素的個數，mbit數組的長度）且哈希函數之間時相互獨立的，哈希函數散列的bit數組M中的位置時完全隨機的。

一個長度為m的bit數組，元素在插入時經過一次哈希散列後bit數組的某個位置的值沒有被置為1的概率為

經過k個哈希函數散列後，還未被置為1的概率為

如果插入n個元素後，該位置還未被置為1的概率為

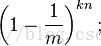
所以被置為1的概率為

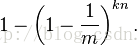
現在判斷一個元素是否在結合中，經過k個函數散列到k個bit數組的不同位置。所有這些位置的值為1的概率——誤判率。

這裏使用了極限

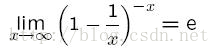
這種計算方法不嚴格，因為前面假設哈希函數和散列後值的分布是相互獨立的。但是，這個假設隨著m和n的增大誤判率更接近真實的誤判率。

Mitzenmacher and Upfal證明無假設情況下的誤判率的期望值相同。

最優的哈希函數個數

既然布隆過濾器將集合映射到位數組中，那麽選多少個hash函數才是錯誤率最低的情況。這裏有兩個互斥的理由：如果哈希函數的個數多，那麽在對一個不屬於集合的元素進行查詢時得到0的概率就大；但另一方面，如果哈希函數的個數少，那麽位數組中的0就多。為了得到最優的哈希函數個數，我們需要根據上一小節中的錯誤率公式進行計算。

誤判率

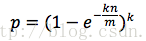
兩邊取自然對數，

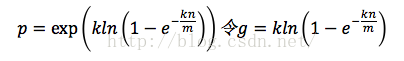
，只要g取最小值，p就能取到最小值。由於p＝e^(-nk/m),我們可以將g改寫為

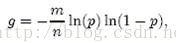
根據對稱法則可以得到當p＝1/2時，也就是k＝ln2*(m/n)時，g取得最小值，在這種情況下，最小的錯誤率p＝（1/2）^k≈(0.6185)^(m/n)。p＝1/2對應著位數組中0和1各半。換句話說，想保持錯誤率低，最好讓位數組有一半還空著。

位數組的大小

在給定n（集合中元素的個數）和錯誤率（最優函數個數k的的錯誤率）的情況下，位數組M的大小計算，在最優k的情況下

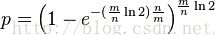
化簡為

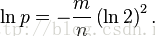
得到

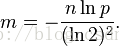
這意味著在錯誤率為p的情況下，布隆過濾器的長度為m才能容納n個元素（以上計算基於n,m->∞）。

布隆過濾器中元素個數的估算

Swamidass & Baldi (2007)給出了布隆過濾器元素個數估算的方法（詳細證明方式參考論文）

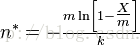
其中，n*表示布隆過濾元素個數的估算值，m表示布隆過濾器的大小，k表示哈希函數的個數，X表示布隆過濾器位值位1的個數。

布隆過濾器的並和交

布隆過濾器可以用來估算兩個集合之間的並合交。一下給出兩個集合之間並的計算方式：

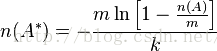
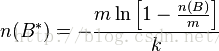
A和B之間的並集的個數為：

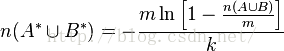
所以A*與B*之間的交集的個數為：

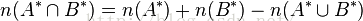
布隆過濾的特性

布隆過濾器能夠容納任意多的元素（誤判率會增加），總是能向布隆過濾器中添加元素，不會報錯（OutMemory等）;

布隆過濾器可以很方便的通過計算機的or \and操作計算兩個集合元素之間的交集（intersection）和並集（union）,但是同樣影響布隆過濾的準確性。

例子

Googlebigtable、apachehbase和apachecassandra使用bloom過濾器判斷是否存在該行（rows）或（colums），以減少對磁盤的訪問，提高數據庫的訪問性能；

比特幣使用布隆過濾判斷錢包是否同步OK。

總結

在計算機這個領域裏，我們常常碰到時間換空間\或空間換時間的情況，為了達到某一方面的性能，犧牲另外一方面。BloomFilter在時間和空間著兩者之間引入了另外一個概念——錯誤率。也就是前文提到的布隆過濾不能準確判斷一個元素是否在集合內（類似的設計還有基數統計法）。引入錯誤率後，極大的節省了存儲空間。

自從Burton Bloom在70年代提出Bloom Filter之後，Bloom Filter就被廣泛用於拼寫檢查和數據庫系統中。近一二十年，伴隨著網絡的普及和發展，Bloom Filter在網絡領域獲得了新生，各種Bloom Filter變種和新的應用不斷出現。可以預見，隨著網絡應用的不斷深入，新的變種和應用將會繼續出現，Bloom Filter必將獲得更大的發展。

Bloom filter(布隆過濾器)概念與原理