影象檢索入門：CVPR2016《Deep Supervised Hashing for Fast Image Retrieval》

阿新 • • 發佈：2018-12-11

TensorFlow程式碼：馬上新增

研究背景

在使用離散化時希望輸出的特徵的關於某個值對稱，所以如《Deep Learning of Binary Hash Codes for Fast Image Retrieval》用了 sigmoid 作為特徵層的輸出的啟用函式，但直接引用 sigmoid 這種非線性函式將不可避免地減慢甚至抑制網路的收斂。解決該問題就是使用正則的方法將輸出約束到某一個範圍內。

研究方法

本文設計了一個新的CNN模型，不是使用單張圖片進行訓練，而是通過輸入成對影象（我們線上的生成影象對，以便在訓練階段可以使用更多的影象對）和影象對應的標籤來進行訓練，輸出是這對影象的Hash值，並設計損失函式用於將相似影象的網路輸出拉到一起，並將不相似影象的輸出推送到很遠的位置，以使得學習到的漢明空間可以很好地逼近影象的語義結構。具體過程如下：

1.設定最後一層全連線層節點數為12，將訓練資料輸入到網路（如下圖所示）中進行預訓練，得到對應資料的12位Hash值；

2.設定最後一層全連線層節點數為24/36/48，利用上一步得到的權重微調，得到對應資料的24/36/48位Hash值；

3.根據得到的Hash值進行影象檢索。

為了避免優化海明空間中的不可微的損失函式，網路輸出放寬到實值，同時強制正則化器來使實值輸出逼近期望的離散值。

1.網路設定

本文的網路模型設定為3個卷積層（卷積層+池化層）和2個全連線層，具體如上圖所示：

conv1：卷積核為5*5*32，步數為1

max_pooling1：卷積核為3*3*32，步數為2

conv2：卷積核為5*5*32，步數為1

average_pooling2：卷積核為3*3*32，步數為2

conv3：卷積核為5*5*64，步數為1

average_pooling3：卷積核為3*3*64，步數為2

fc1：500個節點

fc2：k個節點(Hash值位數)

2.損失函式

初步設計

利用將相似影象的程式碼拉到一起，並且將不相似影象的程式碼彼此分開的思想，損失函式定義如下：

$L\left ( b_{1},b_{2},y \right )=\frac{1}{2}\left ( 1-y \right )D_{h}\left ( b_{1},b_{2} \right )+\frac{1}{2}y\max (m-D_{h}\left ( b_{1},b_{2} \right ),0)$

$\begin{matrix} s.t. & b_{j}\epsilon \left \{ +1,-1 \right \}^{k},j\epsilon \left \{ 1,2 \right \} \end{matrix}$

輸入的影象對 $I_{1},I_{2}$ ，經過網路模型後得到對應的Hash值 $b_{1},b_{2}$ ， $D_{h}\left ( \cdot ,\cdot \right )$ 定義為該影象對 $I_{1},I_{2}$ 的Hash值 $b_{1},b_{2}$ 的漢明距離，m是一個閾值引數；
對於只有單標籤的影象，若該影象對 $I_{1},I_{2}$ 的標籤相同，表示他們是相似的並定義 $y=0$ ；若該影象對 $I_{1},I_{2}$

的標籤不同，表示他們是不相似的並定義 $y=1$ ；
對於多標籤的影象，若該影象對 $I_{1},I_{2}$ 的標籤有一個是相同的，表示他們是相似的並定義 $y=0$ ；若該影象對 $I_{1},I_{2}$ 的標籤沒有一個是相同的，表示他們是不相似的並定義 $y=1$ ；
$\frac{1}{2}\left ( 1-y \right )D_{h}\left ( b_{1},b_{2} \right )$ 表示在 $y=0$ （影象對相似）時，像它們Hash值的漢明距離就是它們之間的損失；
$\frac{1}{2}y\max (m-D_{h}\left ( b_{1},b_{2} \right ),0)$ 表示在 $y=1$ （圖對不相似）時，不相似的影象對距離儘可能的大，從而使得該損失函式儘可能的小。

同時得到整體損失函式的矩陣表達形式： $\pounds =L\left ( b_{i,1},b_{i,2},y_{i} \right )$

$\begin{matrix} s.t. & b_{i,j}\epsilon \left \{ +1,-1 \right \}^{k},i\epsilon \left \{ 1,...,N \right \},j\epsilon \left \{ 1,2 \right \} \end{matrix}$

鬆弛

我們的目標就是最小化損失函式，但是對於上面的約束和其他論文的hashcode約束一樣，都是二值的，離散的，不可導。所以在訓練的時候，不好反向傳播誤差。因此將損失函式更改為如下形式：

$L_{r}\left ( b_{1},b_{2},y \right )=\frac{1}{2}\left ( 1-y \right )\left \| b_{1},b_{2} \right \|_{2}^{2} +\frac{1}{2}y\max (m-\left \| b_{1},b_{2} \right \|_{2}^{2},0)+\alpha \left ( \left \| \left | b_{1} \right |-1 \right \| _{1}+\left \| \left | b_{2} \right |-1 \right \| _{1}\right )$

$\left | \cdot \right |$ 表示逐元素絕對值運算，α是控制正則化器強度的加權引數；
將原來的約束條件 $\begin{matrix} s.t. & b_{j}\epsilon \left \{ +1,-1 \right \}^{k},j\epsilon \left \{ 1,2 \right \} \end{matrix}$ 更改為 $\alpha \left ( \left \| \left | b_{1} \right |-1 \right \| _{1}+\left \| \left | b_{2} \right |-1 \right \| _{1}\right )$ ；
$\left \| \cdot \right \|_{2}^{2}$ 表示L2距離，本文使用L2範數來測量Hash值之間的距離，因為由低階範數產生的子梯度同等地處理具有不同距離的影象對，因此不使用不同距離量級中涉及的資訊。雖然高階規範也是可行的，但同時會產生更多的計算；
$\left \| \cdot \right \|_{1}$ 表示L1正則，對於正則化器，選擇L1範數而不是高階規範，因為其計算成本要低得多，這可以有利地加速訓練過程。

同時得到整體損失函式的矩陣表達形式：

$L_{r}\left ( b_{1},b_{2},y \right )=\sum_{i=1}^{N}\left \{ \frac{1}{2}\left ( 1-y \right )\left \| b_{i,1},b_{i,2} \right \|_{2}^{2} +\frac{1}{2}y\max (m-\left \| b_{i,1},b_{i,2} \right \|_{2}^{2},0)+\alpha \left ( \left \| \left | b_{i,1} \right |-1 \right \| _{1}+\left \| \left | b_{i,2} \right |-1 \right \| _{1}\right ) \right \}$

3.模型訓練

本文使用資料集Cifar10（單標籤）和NUS-WIDE（多標籤），本文主要使用兩種方式來進行訓練網路：

線上生成影象對

為了更好地利用計算資源和儲存空間，本文通過利用每個小批量中的所有資料集來線上生成影象對。為了覆蓋批次中的那些影象對，在每次迭代中，從整個訓練集中隨機選擇訓練影象。通過這樣做，我們的方法減少了儲存整個成對相似性矩陣的需要，因此可以擴充套件到大規模資料集。

預訓練

先在輸出層節點數為12的網路中進行預訓練，再使用學習到的引數微調輸出層節點數為24/36/48的網路。

4.影象檢索

待檢測的影象通過訓練的模型得到對應的Hash值，根據Hash值計算該影象和資料庫中影象的漢明距離，距離越小表示兩影象越相似，否則越不相似。

實驗結果

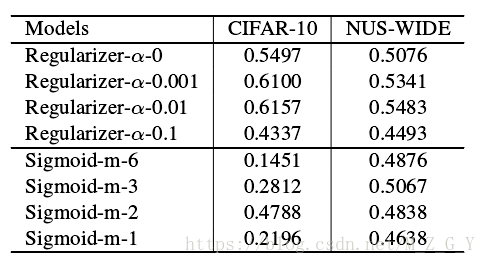
正則引數實驗

在Hahs值位數k = 12基礎上實驗，可以看出當 $\alpha=0.01$ 和 $m=24\left ( m=2\times k \right )$ 時mAP最高。

預訓練實驗

在 $\alpha=0.01$ 和 $m=24\left ( m=2\times k \right )$ 前提下，預訓練可以有效的防止過擬合。

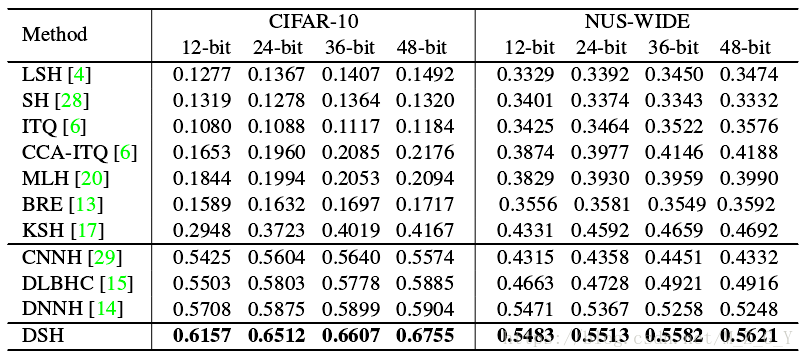
和其他實驗比較

影象檢索入門：CVPR2016《Deep Supervised Hashing for Fast Image Retrieval》

研究背景