正在看《機器學習實戰》這本書的朋友，在看到logistic迴歸的地方，可能會對P78頁的梯度上升演算法程式碼以及P79這裡的這句話弄的一頭霧水：“此處略去了一個簡單的數學推導，我把它留給有興趣的讀者”。這句話就是針對下面這段我貼出來的程式碼中的gradAscent函式說的。

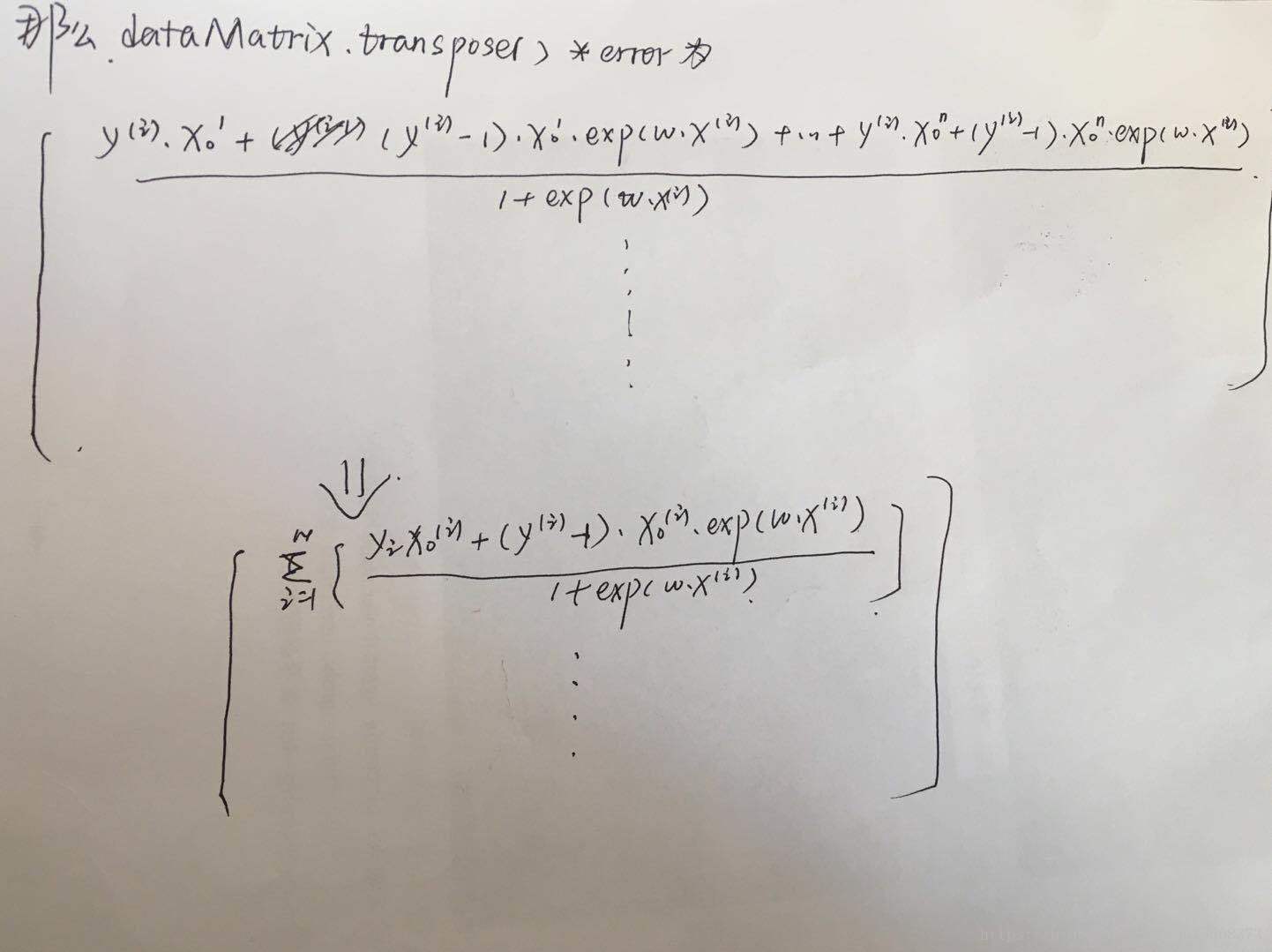
我當時是想不明白為什麼特徵值矩陣的轉置：dataMatrix.transpose()，它與真實類別/預測類別二者之間的差做矩陣乘法得到的結果，就被直接當作梯度了。

於是上網搜了下關於這部分內容的解釋，baidu搜到的前兩條連結裡的內容都是基於均方誤差（最小二乘法）作為代價函式對於此處做的數學解釋。其他的搜尋結果也未給予詳細的數學推導過程。

而看過Andrew.N.G公開課logistic迴歸這一章的朋友，想必不會忘記吳老師關於logistic迴歸的代價函式處的額外補充，有別於線性迴歸，logistic迴歸如果依舊採用均方誤差作代價函式，那麼應用梯度下降法進行優化效果不會很理想（由於非凸，存在區域性最優值），再翻看一下李航老師的《統計學習方法》一書，也能發現logistic迴歸的“策略”也是求取對數似然函式的極大值為目標，而非求取均方誤差函式的極小值。

二來，上述程式碼是“梯度上升演算法”的實現，如果拿均方誤差函式作為代價函式，那豈不是助紂為虐，代價越來越大麼？

基於上述兩點疑問，決定自己做一下數學推導，推導過程如下：


推導過程除了符號複雜一些，真的不難。。。就是單純的求偏導數而已

接下來是對程式碼中的過程進行下數學驗證：


到這裡，我們就可以發現，正常的數學推導得到的梯度跟程式碼中dataMatrix.transpose()*error是一模一樣的。

補充：作者也是剛剛入門機器學習，本著較真的勁兒嘗試著用均方誤差做代價函式，看一看是不是存在很多區域性最優值。。。
以這本書附帶的資料集做為例子，設定了10000個權重向量，觀察一下代價函式的影象。
以下是程式碼：

# -*- coding: utf-8 -*-
"""
Created on Wed Sep 26 19:40:20 2018

@author: _Miracle
本檔案為驗證logistic迴歸使用均方誤差函式作代價函式不可行
"""

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def loadData():
    dataMat = []
    labelMat = []
    fr = open(r'C:\Users\_Miracle\Desktop\machinelearninginaction-master\Ch05\testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(intX):
    return 1.0/(1+np.exp(-intX))


sampleData,classLabel = loadData()
sampleDataMat = np.array(sampleData)

print ('這是特徵資料值(100X2),100個樣本，每個樣本兩個特徵')
print (sampleDataMat)

#比較笨的方法，生成二維普通的list，然後呼叫
m,n = np.shape(sampleDataMat)
newListofList = []
for i in range(m):
    newList = []
    newList.append(classLabel[i])
    newListofList.append(newList)
classLabelMat = np.array(newListofList)

print ('這是每個樣本的類別(100X1)，100個樣本就有100個實際類別')
print (classLabelMat)

a = np.arange(m)
a = np.tile(a,(1,m))
#將a變為形如[[0，1，2，0，1，2，···，0，1，2]]重複arange(100)100次的ndarray
b = np.arange(m)
b = np.tile(b,(m,1))
b = b.transpose()
b = b.reshape(1,10000)
#將b處理成形如[[0,0,0,1,1,1,2,2,2]]這種0-99各重複100次的ndarray
#將a，b處理成這個樣子是為了生成一個2x10000的矩陣，使得有10000種權重搭配的可能
weights = np.vstack((a,b))

#weights是權重，此檔案中假設函式暫定為h(x)=1/1+exp(-w1*x1-w2*x2)
#未加入偏置b(就是w0*x0)，以便作圖直觀一些
#weights為2X10000的均勻序列，為要觀察代價函式的變化

suppose = sigmoid(sampleDataMat.dot(weights))
print ('此處為假設函式輸出的結果')
print (suppose)
print (np.shape(suppose))
print (suppose[0][0])

#隨手檢驗一下假設函式的所有輸出是否有問題
for i in range(len(suppose)):
    for j in range(len(suppose[i])):
        if suppose[i][j]>1 or suppose[i][j]<0:
            print ('有問題')

classLabelMat = np.tile(classLabelMat,(1,10000))
print ('將實際標籤沿著1軸重複10000次，以便一百萬個結果都能做差')
print (classLabelMat)

#下面註釋掉的autoNorm函式為均值歸一化
#加入了特徵縮放會讓影象變得更加平滑一點
#不加入均值歸一化的話，影象震盪的會明顯一些
#想看看加入效果的話，直接開啟註釋即可，無需進行其他操作
'''def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = np.zeros(np.shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - np.tile(minVals,(m,1))
    normDataSet = dataSet/np.tile(ranges,(m,1))
    return normDataSet,ranges,minVals

sampleDataMat,xxx,yyy = autoNorm(sampleDataMat)
'''

def costFunction(a,b):
    #下面為計算代價函式的具體程式碼過程
    #由於已知資料集有100個樣本，遂以下進行重組資料結構的時候直接傳入具體數字而非m了
    a = np.tile(a,(1,100))
    b = np.arange(100)
    b = np.tile(b,(100,1))
    b = b.transpose()
    b = b.reshape(1,10000)
    weights = np.vstack((a,b))
    costConsequence = sigmoid(sampleDataMat.dot(weights))-classLabelMat
    costConsequence = costConsequence**2
    costConsequence = costConsequence.sum(0)/200
    costConsequence = costConsequence.reshape((100,100))
    return costConsequence
 
#橫縱座標為0-99的均勻序列，X為權重w1，Y為權重w2    
X=np.arange(m)
Y=np.arange(m)

#繪製代價函式costFunction(w1,w2)的變化3D圖
cost = costFunction(X,Y)
X,Y=np.meshgrid(X,Y)
fig=plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, cost, rstride = 1, cstride = 1, cmap='rainbow')


    
 

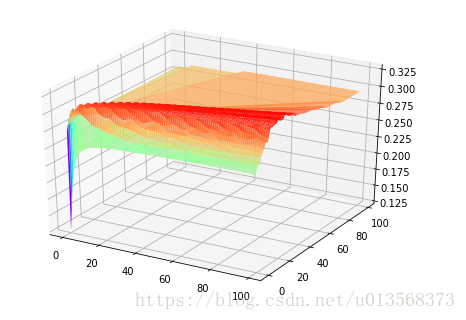
最後是程式碼的執行結果，代價函式的影象（未進行特徵縮放）：

從圖中我們可以看出（儘管不是非常明顯），在很多區域，確實存在多個波動，那麼使用梯度下降等優化演算法時，容易陷入區域性最優解的確是個令人頭疼的問題。