神經網路學習——BP神經網路筆記
神經網路學習,又叫做神經網路的訓練演算法,可以通過計算和更新神經網路本身的權值和閾值,加強網路自身的學習能力。
一.神經元模型
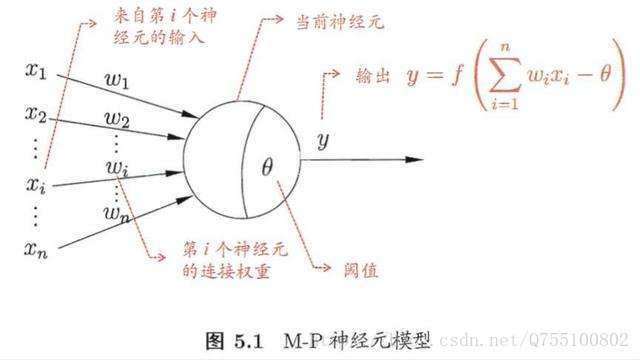
神經網路最基本的模型就是神經元模型,也是神經網路中的簡單單元。神經元常用的簡單模型是M-P神經元模型,如下所示:
閾值:就相當於神經元的興奮電位,當這個神經元的輸入電位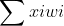 大於這個神經元的閾值時,它就會被啟用,向其他神經元傳送電位,所以輸出
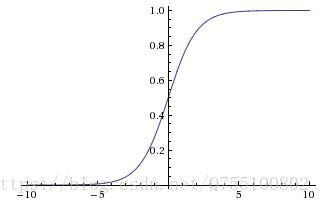
大於這個神經元的閾值時,它就會被啟用,向其他神經元傳送電位,所以輸出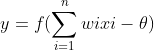 ,而函式f表示的是一個啟用函式,它將函式的輸出值擠壓到(0,1)的範圍之內,函式影象如下
,而函式f表示的是一個啟用函式,它將函式的輸出值擠壓到(0,1)的範圍之內,函式影象如下
其他常用的也有符號函式什麼的,不過不夠光滑。
為了簡化表示,通常我們把閾值 θ記為 −w0,並假想有一個附加的常量輸入 x0=1,那麼我們就可以把神經元的輸入記為 ∑ni=0wixi 或以向量形式寫為 w⋅x,把輸出記為 y=f(∑ni=0wixi)。
把許多個這樣的神經元按一定層次組合,就得到一個神經網路。
二.感知機
感知機由兩層神經元組成,輸入層接受外部訊號後傳給輸出層,輸出層就是M-P神經元,亦稱“閾值邏輯單元”,由閾值的大小將輸入的資料分為多種邏輯組合。感知機的啟用函式 ff 就是之前介紹過的階躍函式,因而我們可以把感知機函式寫為
y=sgn(x)就是我們熟悉的符號函式。還可以把感知機看作是 n 維例項空間中的超平面決策面,對於超平面一側的例項,感知器輸出 1,對於另一側的例項輸出 0,這個決策超平面方程是 w⋅x=0。 那些可以被某一個超平面分割的正反樣例集合稱為線性可分(linearly separable)
所以,給定訓練集,感知機的權重wi和閾值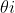 就可以通過學習得到。由上述可以閾值也可以當做一個-1w0的權值,所以學習過程就可以統一為權值的學習。學習規則非常簡單,對訓練樣本(x,y),若當前感知機輸出為
就可以通過學習得到。由上述可以閾值也可以當做一個-1w0的權值,所以學習過程就可以統一為權值的學習。學習規則非常簡單,對訓練樣本(x,y),若當前感知機輸出為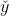 ,則調整公式如下:
,則調整公式如下:
其中,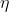 為學習率,若感知機預知正確,則
為學習率,若感知機預知正確,則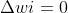 ,感知機不發生變化,否則將根據錯誤的程度進行權重調整。
,感知機不發生變化,否則將根據錯誤的程度進行權重調整。
從上面的知識知道,感知機只有一層功能神經元(所謂功能神經元,就是有閾值的神經元,輸入層是沒有閾值的),學習能力差,只能解決線性問題,甚至不能求解異或這樣的非線性可分的問題。
要解決非線性可分的問題,需要使用多層功能神經元,所以在輸入層和輸出層之間通常會加入一層或多層隱含層,隱含層和輸出層都是具有啟用函式和閾值的功能神經元。更一般的,常見的神經網路是如下圖所示的層次結構,神經元之間不存在同層連線,也不能跨層連線,這樣的神經網路通常被稱為多層前饋神經網路。
單隱層的神經網路是最常見的神經網路,我們的BP神經網路就是這種。已經證明,只需一個包含足夠多的神經元的隱層,多層前饋神經網路就能以任意精度逼近任意複雜度的連續函式,雖然我不知道也不關心怎麼證明的,然而個數的設定仍是未解問題,還得靠試錯法調整。
三.誤差逆傳播演算法——BP演算法
這是一種典型的有導師指導的學習演算法,基本思想就是對一定數量的樣本對(輸入和期望輸出)進行學習,即將樣本的輸入傳入送至網路輸入層的各個神經元,經隱含層和輸出層計算後,輸出層各個神經元輸出對應的預期值,若預期值與期望的輸出之間不滿足誤差精度要求,則從輸出層反向傳播該誤差(注意傳播的是誤差),並通過權值和閾值的修改公式進行修改,使得整個網路的輸出和期望輸出的誤差不斷減小,直到滿足精度為止。
也就是說,BP網路是將網路的輸出與期望輸出間的誤差歸結為權值和閾值的過錯,反向傳播將誤差分攤給各個功能神經元,權值和閾值的調整也要沿著誤差函式下降最快的方向——負梯度方向進行調整,調整公式就是重中之重。
給定一個樣本矩陣,![X=[x1,x2,....xm],Y=[y1,y2,......ym]](https://private.codecogs.com/gif.latex?X%3D%5Bx1%2Cx2%2C....xm%5D%2CY%3D%5By1%2Cy2%2C......ym%5D) ,並且有一個擁有d個輸入神經元,l個輸出神經元,q個隱層神經元的多層前饋神經網路結構,輸出層第j個神經元的閾值
,並且有一個擁有d個輸入神經元,l個輸出神經元,q個隱層神經元的多層前饋神經網路結構,輸出層第j個神經元的閾值
為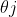 ,隱含層閾值為
,隱含層閾值為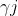 ;輸入層與隱含層的神經元連線為
;輸入層與隱含層的神經元連線為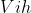 ,隱含層與輸出層的神經元連線為
,隱含層與輸出層的神經元連線為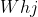 ,則隱含層第h個神經元的輸入為
,則隱含層第h個神經元的輸入為
輸出層第j個神經元接收到的輸入為
Bh為隱層第h個神經元的輸出。對訓練例(xk,yk),假定神經網路的輸出為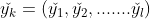
即 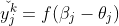
則網路在(xk,yk)上的均方誤差為
這個就是我們要縮小和反向傳播的誤差值,BP是一個迭代學習演算法,在迭代的每一輪中採用廣義的感知機學習規則對引數進行更新和評估,所以,任意引數的更新公式都為
BP演算法基於梯度下降策略,以目標的負梯度方向對引數進行調整,對誤差Ek,給定學習率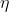 ,有
,有
注意,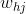 先影響到第j個輸出層神經元的輸入值
先影響到第j個輸出層神經元的輸入值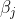 ,再影響到其輸出值
,再影響到其輸出值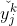 ,然後影響到Ek,這就是整個誤差逆傳遞的過程,有
,然後影響到Ek,這就是整個誤差逆傳遞的過程,有
而
且
所以有
所以聯立幾個式子,有
類似的,所有閾值和權值的更新公式都可以由上述的近似方法得到,有
其中,